Оглавление:
Логарифмические неравенства с постоянными основаниями
Рассмотрим свойства функции 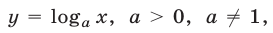 , используемые при решении логарифмических неравенств.
, используемые при решении логарифмических неравенств.
Логарифмическая функция 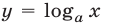 определена при
определена при 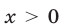 , является возрастающей при
, является возрастающей при  (рис. 24.1) и убывающей при
(рис. 24.1) и убывающей при 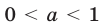 (рис. 24.2), множество значений этой функции — множество
(рис. 24.2), множество значений этой функции — множество 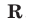 .
.
Простейшие логарифмические неравенства
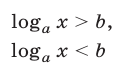
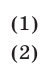
имеют решения при любом 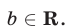
Если  , то неравенство (1) справедливо при
, то неравенство (1) справедливо при 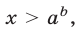 а неравенство (2) является верным при
а неравенство (2) является верным при 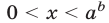 (рис. 24.1).
(рис. 24.1).
Если 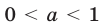 , то множеством решений неравенства (1) является интервал
, то множеством решений неравенства (1) является интервал 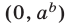 , а неравенство (2) является верным при
, а неравенство (2) является верным при 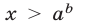 (рис. 24.2). Неравенство
(рис. 24.2). Неравенство
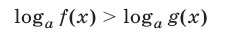
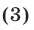
при  равносильно двойному неравенству
равносильно двойному неравенству
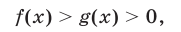
а при 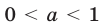 неравенство (3) равносильно неравенству
неравенство (3) равносильно неравенству
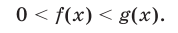
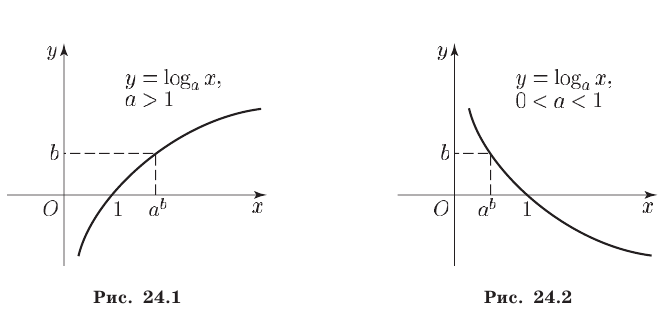
Примеры с решениями
Пример №280.
Решить неравенство 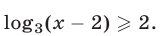
Решение:
Запишем данное неравенство в виде
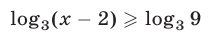
и воспользуемся тем, что логарифмическая функция с основанием, большим единицы, является возрастающей (см. рис. 24.1). Получим 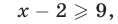 откуда
откуда 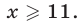
Ответ. 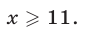
Пример №281.
Решить неравенство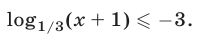
Решение:
Так как 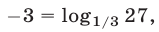 а логарифмическая функция с основанием, меньшим единицы, является убывающей (см. рис. 24.2), то данное неравенство равносильно неравенству
а логарифмическая функция с основанием, меньшим единицы, является убывающей (см. рис. 24.2), то данное неравенство равносильно неравенству 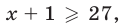 откуда
откуда 
Ответ. 
Пример №282.
Решить неравенство
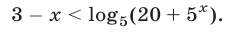
Решение:
Данное неравенство равносильно каждому из следующих неравенств:
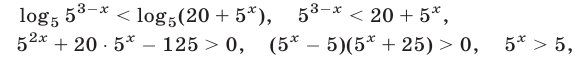
откуда 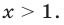
Ответ. 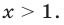
Пример №283.
Решить неравенство 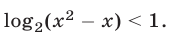
Решение:
Данное неравенство, записанное в виде
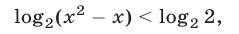
равносильно двойному неравенству
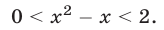
Множество 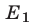 решений неравенства
решений неравенства 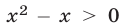 представляет собой объединение промежутков
представляет собой объединение промежутков 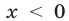 и
и 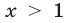 (рис. 24.3), а множество решений неравенства
(рис. 24.3), а множество решений неравенства 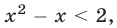 равносильного неравенству
равносильного неравенству 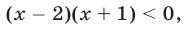 — интервал
— интервал 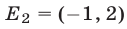 (см. рис. 24.3).
(см. рис. 24.3).

Множество 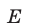 решений исходного неравенства — это пересечение (общая часть) множеств
решений исходного неравенства — это пересечение (общая часть) множеств 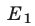 и
и 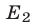 . Следовательно,
. Следовательно, 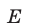 является объединением интервалов
является объединением интервалов 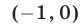 и
и 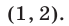
Ответ. 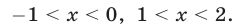
Пример №284.
Решить неравенство
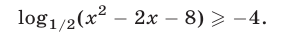
Решение:
Данное неравенство, записанное в виде
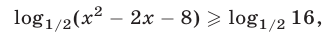
равносильно системе неравенств
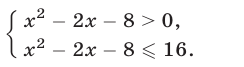
Множество решений первого неравенства этой системы, равносильного неравенству 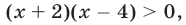 есть объединение промежутков
есть объединение промежутков 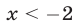 и
и 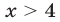 (см. рис. 24.4).
(см. рис. 24.4).

Множество решений второго неравенства системы, равносильного каждому из неравенств 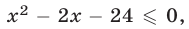
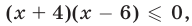 есть отрезок
есть отрезок 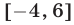 (см. рис. 24.4).
(см. рис. 24.4).
Поэтому множество решений системы неравенств представляет собой объединение промежутков 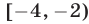 и
и 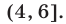
Ответ. 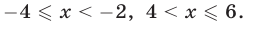
Пример №285.
Решить неравенство
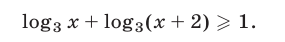
Решение:
Так как 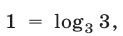 то, заменив сумму логарифмов на логарифм произведения, получим неравенство
то, заменив сумму логарифмов на логарифм произведения, получим неравенство
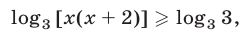
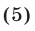
которое неравносильно неравенству (4). Действительно, в неравенстве (4) левая часть определена при 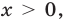 а в неравенстве (5) — при
а в неравенстве (5) — при 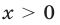 и
и 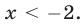 Таким образом, при переходе от (4) к (5) область определения неравенства расширилась. Неравенства (4) и (5) равносильны, если
Таким образом, при переходе от (4) к (5) область определения неравенства расширилась. Неравенства (4) и (5) равносильны, если
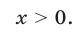
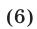
Из (5) следует, что
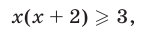
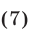
а исходное неравенство (4) равносильно системе (6), (7). Неравенство (7) равносильно каждому из неравенств
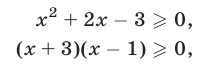
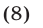
а система (6), (7) равносильна неравенству 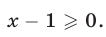
Ответ. 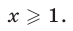
Пример №286.
Решить неравенство
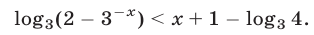
Решение:
Допустимые значения 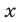 определяются условием
определяются условием
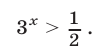
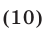
Если выполняется условие (10), то неравенство (9) равносильно каждому из следующих неравенств:
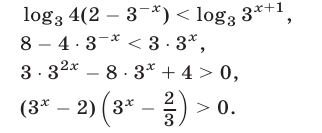
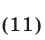
Таким образом, неравенство (9) равносильно системе неравенств (10), (11). Решив неравенство (11), находим, что либо 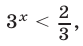 либо
либо 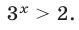
Следовательно, неравенство (9) равносильно совокупности неравенств
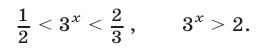
Ответ. 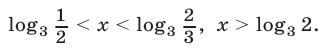
Пример №287.
Решить неравенство
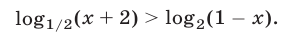
Решение:
Неравенство (12) имеет смысл, если 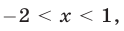 и равносильно неравенству
и равносильно неравенству
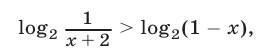
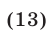
так как 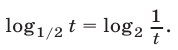
Неравенство (13) на интервале 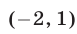 равносильно каждому из неравенств
равносильно каждому из неравенств
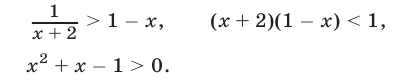
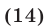
Уравнение 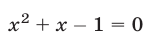 имеет корни
имеет корни 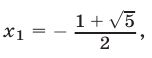
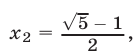 где
где 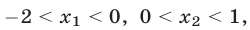 а решениями неравенства (14) являются все числа из интервалов
а решениями неравенства (14) являются все числа из интервалов 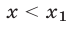 и
и 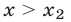 (см. рис. 24.5).
(см. рис. 24.5).

Решениями неравенства (12) являются те и только те числа из интервалов 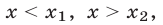 которые принадлежат интервалу
которые принадлежат интервалу 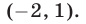
Ответ. 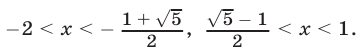
Пример №288.
Решить неравенство
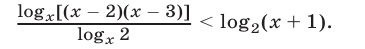
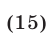
Решение:
Неравенство (15) имеет смысл в том случае, если 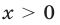 ,
, 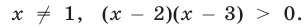 Пусть
Пусть 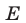 — область определения неравенства (15), тогда множество
— область определения неравенства (15), тогда множество 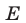 — это объединение интервалов
— это объединение интервалов 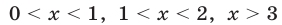 (см. рис. 24.6).
(см. рис. 24.6).

Используя формулу 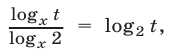 запишем неравенство (15) в виде
запишем неравенство (15) в виде
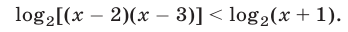
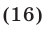
Неравенство (16) на множестве 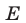 равносильно каждому из неравенств
равносильно каждому из неравенств
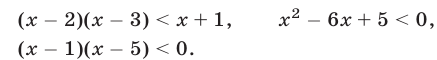
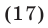
Множество всех решений неравенства (17) — интервал (1,5), а множество всех решений неравенства (15) — пересечение этого интервала и множества 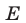 (см. рис. 24.6).
(см. рис. 24.6).
Ответ. 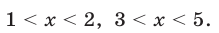
Пример №289.
Решить неравенство
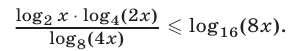
Решение:
Допустимые значения 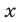 определяются условиями
определяются условиями 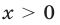 ,
,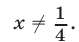 Полагая
Полагая 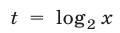 и переходя к логарифмам по основанию 2, запишем неравенство (18) в виде
и переходя к логарифмам по основанию 2, запишем неравенство (18) в виде
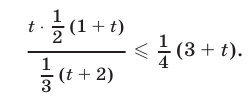
Неравенство (19) равносильно каждому из следующих неравенств :
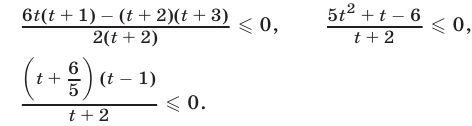
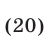
Решив неравенство (20) методом интервалов, получим

Если 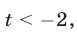 то
то 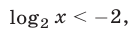 откуда
откуда 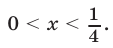
Если 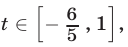 то
то 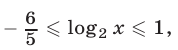 откуда
откуда 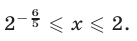
Ответ.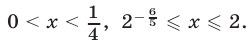
Пример №290.
Решить неравенство
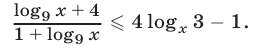
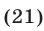
Решение:
Неравенство (21) имеет смысл, если 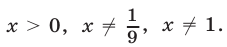 Положим
Положим 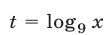 и воспользуемся формулой
и воспользуемся формулой 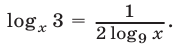 Тогда неравенство (21) примет вид
Тогда неравенство (21) примет вид
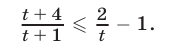
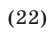
Неравенство (22) равносильно каждому из следующих неравенств :
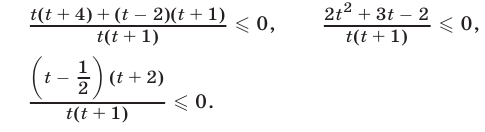
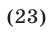
Решив неравенство (23) методом интервалов, получим 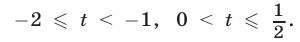 Таким образом, задача сводится к решению неравенств
Таким образом, задача сводится к решению неравенств 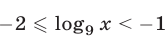 и
и 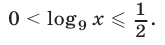
Ответ. 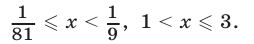
Пример №291.
Решить неравенство
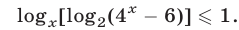
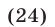
Решение:
Область определения неравенства (24) — это множество 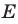 чисел, удовлетворяющих условиям
чисел, удовлетворяющих условиям
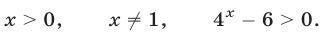
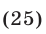
На множестве 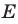 неравенство (24) равносильно неравенству
неравенство (24) равносильно неравенству
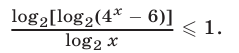
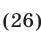
Так как 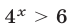 в силу условий (25), то
в силу условий (25), то 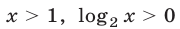 и поэтому неравенство (26) равносильно каждому из неравенств
и поэтому неравенство (26) равносильно каждому из неравенств
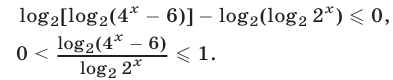
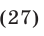
Неравенство (27) равносильно каждой из следующих систем неравенств :
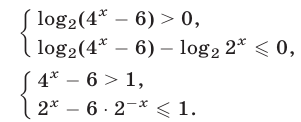

Множество решений неравенства (28) — интервал 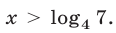 Неравенство (29) равносильно каждому из неравенств
Неравенство (29) равносильно каждому из неравенств
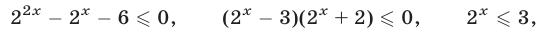
откуда 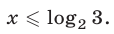
Ответ. 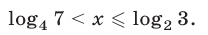
Пример №292.
Решить неравенство
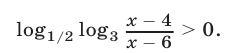
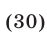
Решение:
Функция 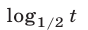 определена при
определена при 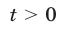 и убывает, а неравенство
и убывает, а неравенство 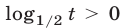 является верным тогда и только тогда, когда
является верным тогда и только тогда, когда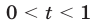 (см. рис. 24.2).
(см. рис. 24.2).
Следовательно, неравенство (30) равносильно неравенству
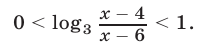
Функция 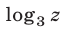 является возрастающей (см. рис. 24.1), а ее значения принадлежат интервалу
является возрастающей (см. рис. 24.1), а ее значения принадлежат интервалу 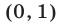 в том и только в том случае, когда
в том и только в том случае, когда 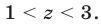
Поэтому неравенство (31) равносильно неравенству
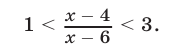
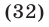
Двойное неравенство (32) можно записать в виде следующей системы рациональных неравенств:
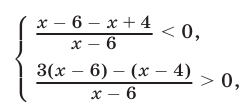
которая равносильна системе
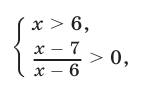
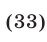
откуда находим, что 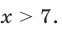
Ответ. 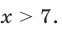
Замечание. При решении неравенства (30) многие абитуриенты допустили ошибку: вместо неравенства (31) записывали неравенство
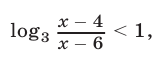
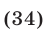
затем получали неравенство (33) и, решив его с учетом ОДЗ неравенства (34), приходили к выводу, что множество решений неравенства (30) — объединение промежутков 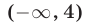 и
и 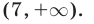
Пример №293.
Решить неравенство
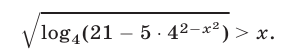
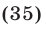
Решение:
Область допустимых значений неравенства (35) найдем из неравенства
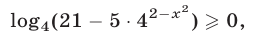
равносильного каждому из следующих неравенств:
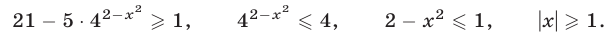
Рассмотрим два случая: 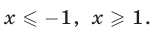
1) Если 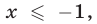 то левая часть неравенства (35) определена и принимает неотрицательные значения, а правая часть отрицательна. Поэтому значения
то левая часть неравенства (35) определена и принимает неотрицательные значения, а правая часть отрицательна. Поэтому значения 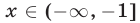 являются решениями неравенства (35).
являются решениями неравенства (35).
2) Если 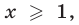 то неравенство (35) равносильно каждому из следующих неравенств:
то неравенство (35) равносильно каждому из следующих неравенств:
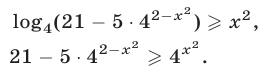
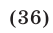
Пусть 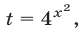 тогда неравенство (36) примет вид
тогда неравенство (36) примет вид
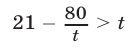 или
или 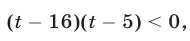
откуда 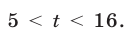 Решив неравенство
Решив неравенство 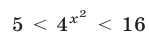 на множестве
на множестве 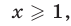 получим
получим
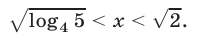
Ответ. 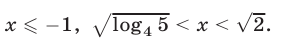
Пример №294.
Решить неравенство
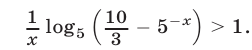
Решение:
1) Пусть  тогда неравенство (37) равносильно каждому из следующих неравенств:
тогда неравенство (37) равносильно каждому из следующих неравенств:
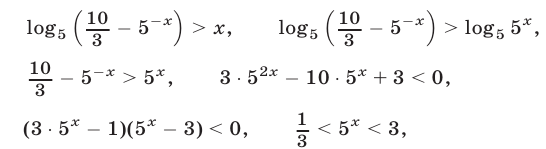
откуда, учитывая условие  , получаем
, получаем 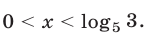
2) Аналогично, при 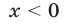 неравенство (37) равносильно каждому из неравенств
неравенство (37) равносильно каждому из неравенств
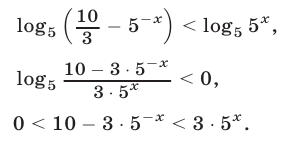
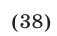
Неравенство (38) равносильно системе неравенств
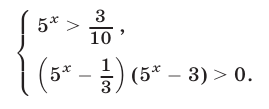
Решив эту систему с учетом условия 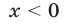 , получим
, получим 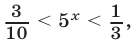 откуда
откуда
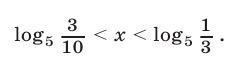
Ответ. 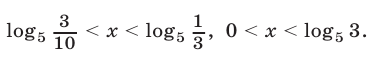
Пример №295.
Решить неравенство
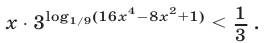
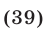
Решение:
Так как 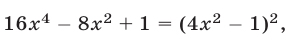 то допустимые значения
то допустимые значения 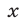 определяются условием
определяются условием
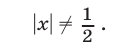
Воспользуемся равенством 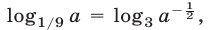 тогда неравенство (39) можно заменить (при условии (40)) каждым из следующих неравенств:
тогда неравенство (39) можно заменить (при условии (40)) каждым из следующих неравенств:
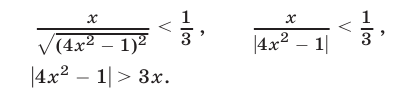
Левая часть неравенства (41) неотрицательна, поэтому все значения 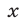 такие, что
такие, что 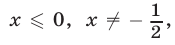 являются решениями неравен-ства (39).
являются решениями неравен-ства (39).
Пусть 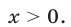 Рассмотрим два случая:
Рассмотрим два случая: 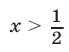 и
и 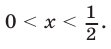
Если 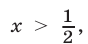 то
то 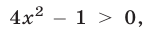 и неравенство (41) равносильно каждому из неравенств
и неравенство (41) равносильно каждому из неравенств
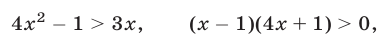
откуда, учитывая, что 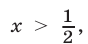 получаем
получаем 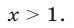
Если 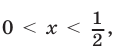 то
то 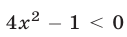 и неравенство (41) равносильно каждому из неравенств
и неравенство (41) равносильно каждому из неравенств
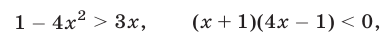
откуда 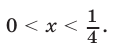
Ответ. 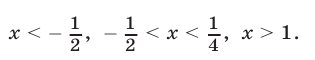
Этот материал взят со страницы решения задач с примерами по всем темам предмета математика:
Возможно вам будут полезны эти страницы:

