Оглавление:
Задачи на сплавы и смеси
Рассмотрим задачи с использованием понятий «процентное содержание», «концентрация», где речь идет о получении сплавов, растворов или смесей.
В таких задачах предполагается, что:
1) все получающиеся сплавы, смеси, растворы однородны;
2) при слиянии двух растворов, имеющих данные объемы, получается смесь, объем которой равен сумме этих объемов.
Примеры с решениями
Пример №202.
От двух кусков сплава с различным процентным содержанием меди отрезали по куску равной массы и каждую из отрезанных частей сплавили с остатками другого куска. В новых сплавах процентное содержание меди стало одинаковым. Найти массу каждого из отрезанных кусков, если масса первого сплава 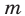 кг, а масса второго
кг, а масса второго 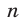 кг.
кг.
Решение:
Первый способ. Назовем для краткости сплавом А первый сплав, а сплавом В — второй сплав. Пусть масса меди в 1 кг сплава А равна 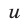 кг, а в 1 кг сплава В равна
кг, а в 1 кг сплава В равна 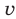 кг. Тогда в первом слитке (новом сплаве) содержится
кг. Тогда в первом слитке (новом сплаве) содержится 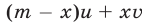 кг меди , и поэтому в 1 кг первого слитка содержится
кг меди , и поэтому в 1 кг первого слитка содержится 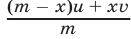 кг меди, где
кг меди, где 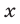 — масса каждого из отрезанных кусков. Аналогично, в 1 кг второго слитка содержится
— масса каждого из отрезанных кусков. Аналогично, в 1 кг второго слитка содержится 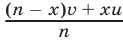 кг меди.
кг меди.
Приравнивая два найденных выражения, получаем уравнение
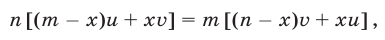
которое можно представить в виде
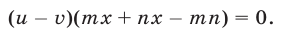
Так как сплавы А и В имеют различное процентное содержание меди, то 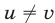 , и поэтому
, и поэтому 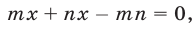 откуда
откуда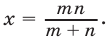
Ответ. Масса каждого из кусков равна 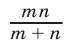 кг.
кг.
Второй способ. Из двух вновь полученных сплавов (слитков) первый содержит 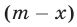 кг сплава А и
кг сплава А и 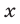 кг сплава В, а второй —
кг сплава В, а второй — 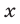 кг сплава А и
кг сплава А и 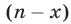 кг сплава В. По условию процентное содержание меди в обоих слитках одинаково. Это возможно лишь тогда, когда в двух слитках массы сплава А и сплава В пропорциона-льны, т. е.
кг сплава В. По условию процентное содержание меди в обоих слитках одинаково. Это возможно лишь тогда, когда в двух слитках массы сплава А и сплава В пропорциона-льны, т. е.
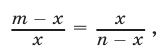
откуда 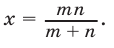
Пример №203.
Сосуд содержит 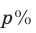 — ный раствор кислоты. Из него отлили
— ный раствор кислоты. Из него отлили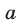 литров и добавили то же количество
литров и добавили то же количество 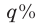 — ного раствора кислоты
— ного раствора кислоты 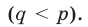 Затем после перемешивания эту операцию повторили еще
Затем после перемешивания эту операцию повторили еще  раз, после чего получился
раз, после чего получился 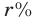 — ный раствор кислоты. Найти объем сосуда.
— ный раствор кислоты. Найти объем сосуда.
Решение:
Пусть 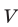 — объем сосуда,
— объем сосуда, 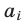 — процентное содержание кислоты в сосуде после
— процентное содержание кислоты в сосуде после 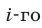 перемешивания
перемешивания 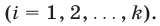 Тогда
Тогда
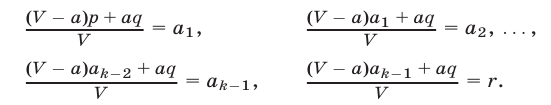
Положим 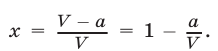 Умножив
Умножив 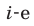 равенство на
равенство на 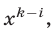 где
где 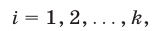 и сложив почленно полученные равенства, находим
и сложив почленно полученные равенства, находим
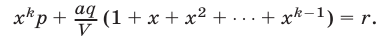
Используя формулу суммы геометрической прогрессии, получаем
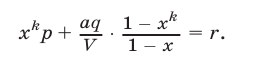
Так как 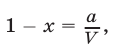 то
то
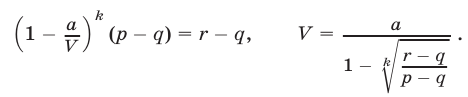
Ответ. 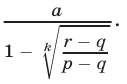
Этот материал взят со страницы решения задач с примерами по всем темам предмета математика:
Возможно вам будут полезны эти страницы:
| Алгебраические системы с тремя неизвестными с примерами решения |
| Задачи на движение с примерами решения |
| Задачи на совместную работу с примерами решения |
| Примеры решения систем показательных уравнений |

