Оглавление:
Задачи на движение
При решении таких задач принято считать, что:
1) движение является равномерным (скорость постоянна и положительна), если не оговорено противное;
2) скорость тела при движении по течению реки равна 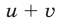 , а при движении против течения равна
, а при движении против течения равна 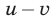 , где
, где 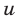 — собственная скорость тела (скорость в стоячей воде);
— собственная скорость тела (скорость в стоячей воде); 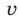 — скорость течения реки; плот движется со скоростью течения реки.
— скорость течения реки; плот движется со скоростью течения реки.
При составлении уравнений в задачах на движение часто используются следующие очевидные утверждения:
1) если два тела, находящиеся перед началом движения на расстоянии 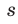 , движутся навстречу друг другу со скоростями
, движутся навстречу друг другу со скоростями 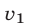 и
и 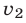 , то время, через которое они встретятся, равно
, то время, через которое они встретятся, равно 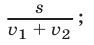
2) если два тела, находящиеся перед началом движения на расстоянии 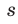 , движутся в одном направлении со скоростями
, движутся в одном направлении со скоростями 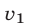 и
и 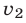 , где
, где  , то время, через которое второе тело (его скорость
, то время, через которое второе тело (его скорость 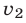 ) догонит первое, равно
) догонит первое, равно 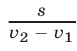 .
.
Примеры с решениями
Пример №194.
Пешеход и велосипедист отправляются одновременно из пункта  в пункт
в пункт  . В пункте
. В пункте  велосипедист поворачивает обратно и встречает пешехода через 20 мин после начала движения. Не останавливаясь, велосипедист доезжает до пункта
велосипедист поворачивает обратно и встречает пешехода через 20 мин после начала движения. Не останавливаясь, велосипедист доезжает до пункта  , поворачивает обратно и догоняет пешехода через 10 мин после первой встречи. За какое время пешеход пройдет путь от
, поворачивает обратно и догоняет пешехода через 10 мин после первой встречи. За какое время пешеход пройдет путь от  до
до  ?
?
Решение:
Пусть 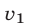 и
и 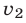 — скорости (в километрах в час) соответственно пешехода и велосипедиста,
— скорости (в километрах в час) соответственно пешехода и велосипедиста, 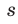 — путь
— путь 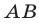 (в километрах) . Так как пешеход и велосипедист встретились через
(в километрах) . Так как пешеход и велосипедист встретились через 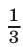 ч, пройдя вдвоем путь
ч, пройдя вдвоем путь 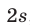 , то
, то
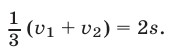
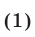
За полчаса, истекших от начала движения до того момента, когда велосипедист догнал пешехода, разность пройденных ими расстояний была равна 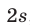 , т. е.
, т. е.
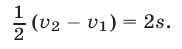
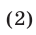
Запишем систему уравнений (1), (2) в виде f Vi + vo = 6s,
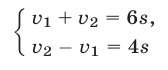
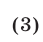
и вычтем из первого уравнения системы (3) второе. Получим 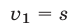 , откуда найдем искомую величину
, откуда найдем искомую величину 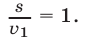
Ответ. За 1 ч.
Пример №195.
Пристань  находится выше по течению реки, чем пристань
находится выше по течению реки, чем пристань  . Из
. Из  и
и  одновременно навстречу друг другу начали движение плот и моторная лодка. Достигнув пристани
одновременно навстречу друг другу начали движение плот и моторная лодка. Достигнув пристани  , моторная лодка немедленно повернула обратно и догнала плот в тот момент, когда он проплыл
, моторная лодка немедленно повернула обратно и догнала плот в тот момент, когда он проплыл 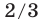 расстояния между
расстояния между  и
и  .
.
Найти время, которое затрачивает плот на путь из  в
в  , если моторная лодка проплывает из
, если моторная лодка проплывает из  в
в  и обратно за Зч.
и обратно за Зч.
Решение:
Пусть 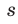 — расстояние между пунктами
— расстояние между пунктами  и
и  , и — скорость течения реки,
, и — скорость течения реки, 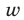 — скорость моторной лодки в стоячей воде. Тогда
— скорость моторной лодки в стоячей воде. Тогда
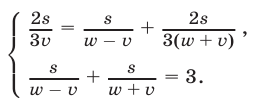
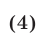
Полагая 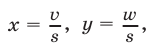 запишем систему (4) в виде
запишем систему (4) в виде
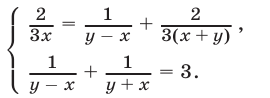
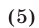
Первое из уравнений системы (5) приводится к однородному уравнению 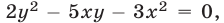 откуда
откуда 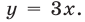 Подставив это выражение во второе уравнение системы (5), получаем
Подставив это выражение во второе уравнение системы (5), получаем 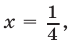 откуда
откуда 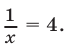
Ответ. 4 ч.
Пример №196.
Из пункта  в пункт
в пункт  вышел пешеход. Вслед за ним через 2 ч из пункта
вышел пешеход. Вслед за ним через 2 ч из пункта  выехал велосипедист, а еще через 30 мин — мотоциклист. Все участники движения перемещались равномерно и без остановок.
выехал велосипедист, а еще через 30 мин — мотоциклист. Все участники движения перемещались равномерно и без остановок.
Через некоторое время после выезда мотоциклиста оказалось, что все трое преодолели одинаковую часть пути от  до
до  . На сколько минут раньше пешехода прибыл в пункт
. На сколько минут раньше пешехода прибыл в пункт  велосипедист, если пешеход прибыл туда на 1 ч позже мотоциклиста?
велосипедист, если пешеход прибыл туда на 1 ч позже мотоциклиста?
Решение:
Первый способ. Пусть 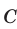 — точка на пути
— точка на пути 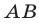 , в которой одновременно оказались участники движения,
, в которой одновременно оказались участники движения, 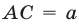 ,
, 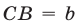 ;
; 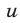 ,
, 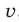 ,
, 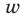 — скорости пешехода, велосипедиста и мотоциклиста соответственно,
— скорости пешехода, велосипедиста и мотоциклиста соответственно, 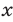 — искомое время. Используя условия задачи, составляем систему уравнений
— искомое время. Используя условия задачи, составляем систему уравнений
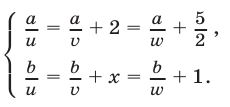
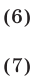
Из (7) находим
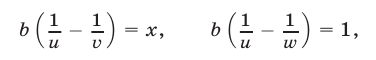
откуда
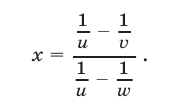
Далее, из (6) получаем
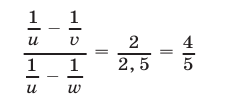
и следовательно , 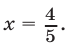
Ответ. 48 мин.
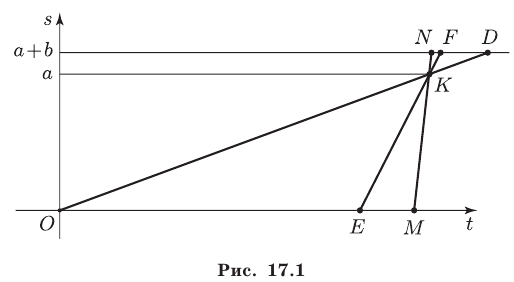
Второй способ. Рассмотрим координатную плоскость, по оси абсцисс будем откладывать время 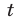 , а по оси ординат — пройденный путь
, а по оси ординат — пройденный путь 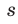 (рис. 17.1).
(рис. 17.1).
Пусть отрезки 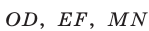 — графики движения пешехода, велосипедиста и мотоциклиста соответственно. По условию эти отрезки имеют общую точку
— графики движения пешехода, велосипедиста и мотоциклиста соответственно. По условию эти отрезки имеют общую точку 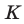 с ординатой
с ординатой 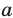 ,
, 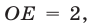
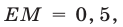
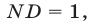 точки
точки 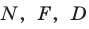 лежат на прямой
лежат на прямой 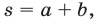
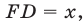 где
где 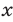 — искомое время.
— искомое время.
Так как  то
то 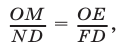 откуда
откуда
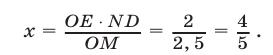
Пример №197.
Автомобилист и велосипедист, выехавшие одновременно соответственно из пунктов  и
и  , совершают безостановочное движение между этими пунктами. Доехав до пункта
, совершают безостановочное движение между этими пунктами. Доехав до пункта  и повернув назад, автомобилист догнал велосипедиста через
и повернув назад, автомобилист догнал велосипедиста через  ч. после их первой встречи. Сколько времени после первой встречи ехал велосипедист до пункта
ч. после их первой встречи. Сколько времени после первой встречи ехал велосипедист до пункта  , если к тому моменту, когда его обогнал автомобилист, он проехал
, если к тому моменту, когда его обогнал автомобилист, он проехал 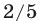 пути от
пути от  до
до  ?
?
Решение:
Первый способ. Пусть 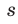 — расстояние между пунктами
— расстояние между пунктами  и
и  ,
, 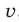 и
и 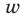 — скорости автомобиля и велосипедиста соответственно,
— скорости автомобиля и велосипедиста соответственно, 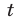 — время (в часах) от начала движения до первой встречи. Тогда
— время (в часах) от начала движения до первой встречи. Тогда
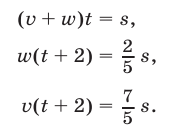
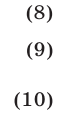
Требуется найти величину 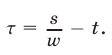 Разделив почленно уравнения (10) и (9), получим
Разделив почленно уравнения (10) и (9), получим
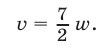
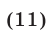
Из (8) и (11) следует, что
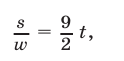
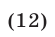
а из (9) находим
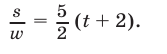
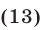
Наконец, из равенств (12) и (13) получаем 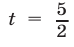 и
и 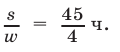
Следовательно,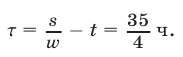
Ответ. 8 ч 45 мин.
Второй способ. Решим задачу, не составляя систему уравнений. От начала движения до того момента, когда автомобилист обогнал велосипедиста, они проехали 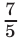 и
и 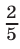 — пути от
— пути от  до
до  . Поэтому отношение их скоростей равно
. Поэтому отношение их скоростей равно 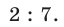
Следовательно, к моменту первой встречи участники движения проехали 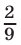 и
и 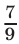 пути от
пути от  до
до . Но, затратив на дорогу еще
. Но, затратив на дорогу еще  ч, велосипедист проезжает
ч, велосипедист проезжает 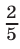 всего пути. Значит, за 1ч он проезжает
всего пути. Значит, за 1ч он проезжает 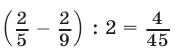 пути. Оставшуюся после первой встречи часть пути
пути. Оставшуюся после первой встречи часть пути 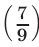 велосипедист проедет за
велосипедист проедет за 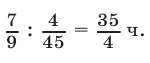
Пример №198.
Дорога проходит через пункты  и
и . Велосипедист выехал из
. Велосипедист выехал из  по направлению к
по направлению к . Одновременно с ним из пункта
. Одновременно с ним из пункта  вышли с равными скоростями два пешехода: первый — в пункт
вышли с равными скоростями два пешехода: первый — в пункт  , а второй — в противоположном направлении. Велосипедист проехал от
, а второй — в противоположном направлении. Велосипедист проехал от  до
до  за 0,5ч и, продолжая движение, догнал второго пешехода. Это произошло через 1,2 ч после встречи велосипедиста с первым пешеходом. Определить время движения велосипедиста от начала движения до встречи с первым пешеходом.
за 0,5ч и, продолжая движение, догнал второго пешехода. Это произошло через 1,2 ч после встречи велосипедиста с первым пешеходом. Определить время движения велосипедиста от начала движения до встречи с первым пешеходом.
Решение:
Пусть 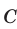 — место встречи велосипедиста с первым пешеходом (рис. 17.2).
— место встречи велосипедиста с первым пешеходом (рис. 17.2).
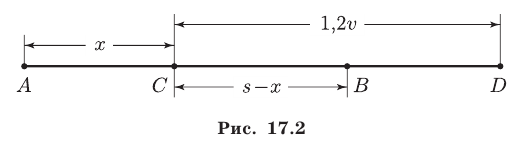
Пусть 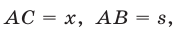
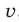 — скорость велосипедиста,
— скорость велосипедиста, 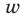 — скорость каждого из пешеходов. Тогда искомое время
— скорость каждого из пешеходов. Тогда искомое время
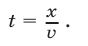
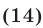
Согласно условию задачи имеем
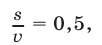
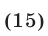
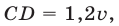 где
где 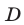 — место (пункт), где велосипедист догнал второго пешехода, вышедшего из
— место (пункт), где велосипедист догнал второго пешехода, вышедшего из  (в направлении
(в направлении 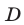 ). Так как велосипедист и первый пешеход вышли одновременно, то время, в течение которого они находились в пути до встречи в
). Так как велосипедист и первый пешеход вышли одновременно, то время, в течение которого они находились в пути до встречи в 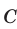 , составляет
, составляет
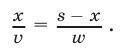
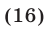
Расстояние 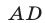 велосипедист преодолел за
велосипедист преодолел за 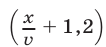 ч, а второй пешеход за это время прошел
ч, а второй пешеход за это время прошел 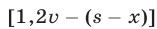 км со скоростью
км со скоростью 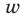 . Следовательно,
. Следовательно,
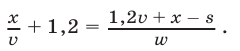
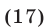
Уравнение (16) в силу (14) и (15) можно записать так:
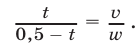
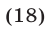
Аналогично, используя равенства (14) и (15), преобразуем уравнение (17):
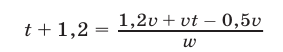
или
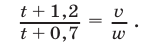
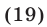
Из (18) и (19) следует, что
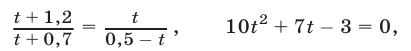
откуда 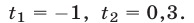
Ответ. 0,3 ч.
Пример №199.
Из пунктов  и
и  навстречу друг другу вышли одновременно два поезда. Каждый из них двигался сначала равноускоренно (начальные скорости поездов равны нулю, ускорения различны), а затем, достигнув некоторой скорости, — равномерно. Отношение скоростей равномерного движения поездов равно
навстречу друг другу вышли одновременно два поезда. Каждый из них двигался сначала равноускоренно (начальные скорости поездов равны нулю, ускорения различны), а затем, достигнув некоторой скорости, — равномерно. Отношение скоростей равномерного движения поездов равно 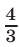 . В момент встречи поезда имели равные скорости, а в пункты
. В момент встречи поезда имели равные скорости, а в пункты  и
и  прибыли одновременно. Найти отношение ускорений поездов.
прибыли одновременно. Найти отношение ускорений поездов.
Решение:
Пусть 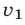 и
и 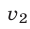 — скорости равномерного движения первого и второго поездов,
— скорости равномерного движения первого и второго поездов, 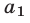 и
и 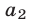 — их ускорения. Предположим, что
— их ускорения. Предположим, что 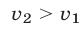 , тогда
, тогда
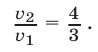
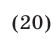
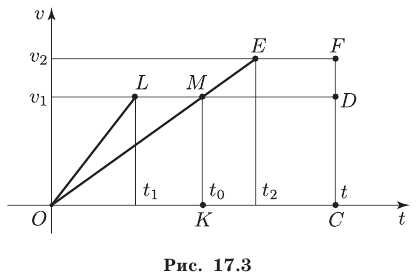
Графики скоростей поездов как функций времени изображены на рис. 17.3.
Здесь 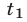 и
и 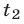 — время равноускоренного движения поездов,
— время равноускоренного движения поездов, 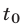 — момент их встречи,
— момент их встречи, 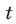 — время прохождения пути каждым из поездов. Заметим, что
— время прохождения пути каждым из поездов. Заметим, что 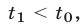 а
а 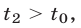 так как
так как 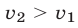 и в момент
и в момент 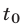 поезда имели равные скорости.
поезда имели равные скорости.
Из равенств 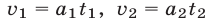 и условия (20) следует, что
и условия (20) следует, что
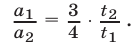
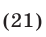
Таким образом, для решения задачи нужно найти отношение 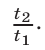
По условию в момент 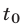 поезда имели равные скорости. Следовательно,
поезда имели равные скорости. Следовательно,
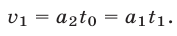
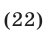
Из (22) и (20) находим
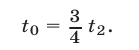
Пусть 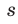 — все расстояние, пройденное каждым из поездов, тогда величина
— все расстояние, пройденное каждым из поездов, тогда величина 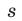 равна площади каждой из трапеций
равна площади каждой из трапеций  и
и  (рис. 17.3), т. е.
(рис. 17.3), т. е.
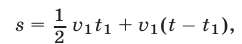
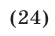
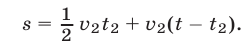
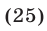
Из равенств (24), (25) и (20) находим
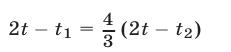
или
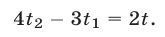
Итак, получены уравнения (23) и (26), связывающие 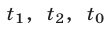 и
и 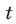 . Не хватает еще одного уравнения. Такое уравнение (и в этом ключ к решению задачи) мы получим, заметив, что сумма расстояний
. Не хватает еще одного уравнения. Такое уравнение (и в этом ключ к решению задачи) мы получим, заметив, что сумма расстояний 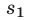 и
и 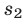 , пройденных поездами до встречи, равна
, пройденных поездами до встречи, равна 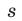 .
.
Так как
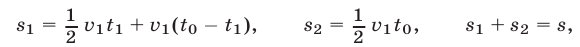
то
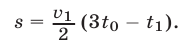
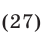
Из (24), (27) и (23) следует, что 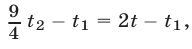 т.е.
т.е.
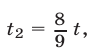
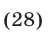
а из (26) и (28) получаем
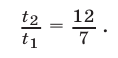
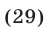
Наконец, из равенств (21) и (29) находим, что 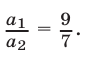
Ответ. 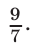
Пример №200.
Два велосипедиста движутся по кольцевой велотрассе длины 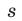 ,
, 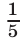 часть которой проходит по стадиону, а оставшаяся часть — по городским улицам. Скорость первого велосипедиста на стадионе равна
часть которой проходит по стадиону, а оставшаяся часть — по городским улицам. Скорость первого велосипедиста на стадионе равна 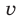 , а на городских улицах равна
, а на городских улицах равна 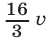 . Скорость второго велосипедиста на стадионе равна
. Скорость второго велосипедиста на стадионе равна 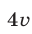 , а на городских улицах
, а на городских улицах 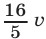 . Велосипедисты одновременно въезжают на стадион. Через какое время после этого один из них впервые совершит обгон другого?
. Велосипедисты одновременно въезжают на стадион. Через какое время после этого один из них впервые совершит обгон другого?
Решение:
Первый велосипедист проезжает полный круг за время
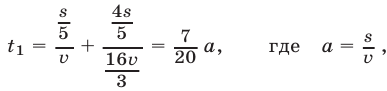
а второй — за время
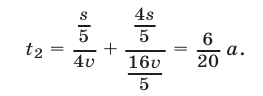
Поэтому второй велосипедист догонит первого, если проедет на круг больше, чем первый, причем это произойдет на стадионе, поскольку там скорость второго больше, чем у первого.
Пусть 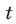 — время от начала движения до момента, когда второй совершит обгон первого;
— время от начала движения до момента, когда второй совершит обгон первого; 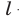 — число целых кругов, пройденных до обгона вторым велосипедистом;
— число целых кругов, пройденных до обгона вторым велосипедистом; 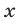 — часть пути по стадиону, пройденная велосипедистами после
— часть пути по стадиону, пройденная велосипедистами после 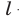 кругов, пройденных вторым.
кругов, пройденных вторым.
Так как на полный круг первый затрачивает на 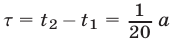 больше, чем второй, то второй, отрываясь от первого, догонит первого, когда выигрыша во времени будет достаточно, чтобы второй проехал круг. Поэтому второму достаточно проехать
больше, чем второй, то второй, отрываясь от первого, догонит первого, когда выигрыша во времени будет достаточно, чтобы второй проехал круг. Поэтому второму достаточно проехать 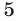 полных кругов
полных кругов 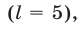 чтобы затем на стадионе обогнать первого. Из условия равенства времени
чтобы затем на стадионе обогнать первого. Из условия равенства времени 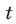 движения каждого его участника с учетом пройденного пути получаем систему уравнений
движения каждого его участника с учетом пройденного пути получаем систему уравнений
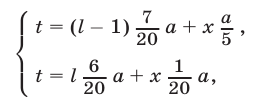
откуда (при 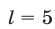 ) находим
) находим
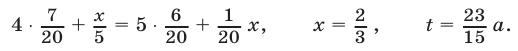
Ответ. 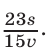
Пример №201.
Катер по реке и автобус по дороге, идущей вдоль берега реки, отправляются одновременно из пункта А в пункт В и совершают безостановочное движение между А и В. Первая их встреча произошла, когда автобус прошел 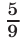 — всего расстояния от А до В, а вторая встреча — когда автобус после первого захода в В проехал всего расстояния от В до А. Первый раз в пункт В автобус прибыл на 16 мин позже катера. Через сколько часов после начала движения автобус и катер окажутся одновременно в пункте А, если скорость катера в неподвижной воде и скорость автобуса постоянны ?
— всего расстояния от А до В, а вторая встреча — когда автобус после первого захода в В проехал всего расстояния от В до А. Первый раз в пункт В автобус прибыл на 16 мин позже катера. Через сколько часов после начала движения автобус и катер окажутся одновременно в пункте А, если скорость катера в неподвижной воде и скорость автобуса постоянны ?
Решение:
Первый способ. Пусть 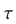 и
и 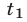 — время (в часах), за которое проходят путь АВ автобус и катер соответственно, a
— время (в часах), за которое проходят путь АВ автобус и катер соответственно, a 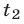 время, за которое катер проходит путь ВА,
время, за которое катер проходит путь ВА, 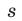 — расстояние АВ.
— расстояние АВ.
До первой встречи в пункте С автобус прошел путь 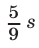 за время
за время 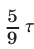 . Такое же время катер затратил на АВ и путь ВС, равный
. Такое же время катер затратил на АВ и путь ВС, равный 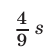 . Следовательно,
. Следовательно,
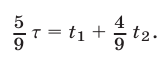
До второй встречи автобус затратил время 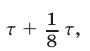 а катер — время
а катер — время 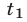 (на АВ), затем
(на АВ), затем 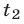 (на ВА) и еще —
(на ВА) и еще — 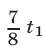 . Значит,
. Значит,
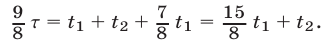
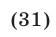
По условию, автобус первый раз прибыл в В на 16 мин (на 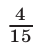 ч) позже катера, т. е.
ч) позже катера, т. е.
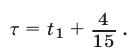
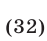
Решив систему (30)-(32) находим
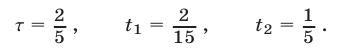
Автобус оказывается в пункте А, преодолев (четное число 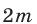 раз) путь от А до В и затратив время
раз) путь от А до В и затратив время 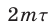 . Катер окажется в пункте А, совершив
. Катер окажется в пункте А, совершив 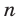 рейсов от А до В и
рейсов от А до В и 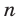 рейсов от В до А и затратив время
рейсов от В до А и затратив время 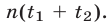 Одновременно в пункте А автобус и катер окажутся лишь в том случае, когда найдутся
Одновременно в пункте А автобус и катер окажутся лишь в том случае, когда найдутся 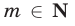 и
и 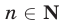 такие, что
такие, что 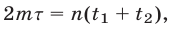 т. е.
т. е.
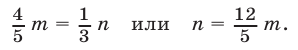
Так как 12 и 5 — взаимно простые числа, то число 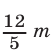 является целым только в том случае, когда
является целым только в том случае, когда 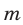 делится на 5. Наименьшее возможное число
делится на 5. Наименьшее возможное число 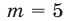 и тогда
и тогда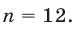
Итак, автобус и катер первый раз одновременно окажутся в пункте А, если автобус сделает 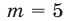 рейсов (катер—12) и затратит время
рейсов (катер—12) и затратит время 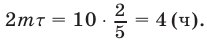
Ответ. Через 4 ч.
Второй способ. Пусть 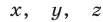 — скорости соответственно катера в стоячей воде, автобуса и течения реки,
— скорости соответственно катера в стоячей воде, автобуса и течения реки, 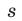 — расстояние от А до В (река течет от А к В, скорость — в километрах в минуту). Тогда, учитывая, что до первой и второй встречи катер и автобус затратили одинаковое время, получаем
— расстояние от А до В (река течет от А к В, скорость — в километрах в минуту). Тогда, учитывая, что до первой и второй встречи катер и автобус затратили одинаковое время, получаем
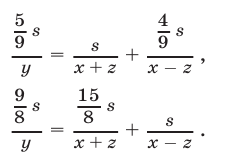

Так как катер пришел в пункт В на 16 мин раньше автобуса, то
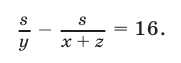
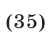
Введем следующие обозначения: 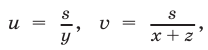
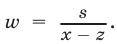
Тогда система (33)—(35) примет вид
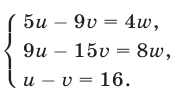
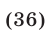
Линейная система (36) имеет решение 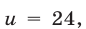
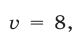
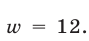 Время, затраченное катером на путь от А до В и обратно, равно
Время, затраченное катером на путь от А до В и обратно, равно 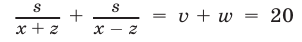 (мин), а время, затраченное автобусом на тот же путь, равно
(мин), а время, затраченное автобусом на тот же путь, равно 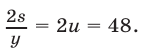 Одновременно автобус и катер первый раз окажутся в пункте А через целое число поездок, поэтому искомое время есть наименьшее общее кратное чисел 48 и 20 и равно 240 мин, т. е. 4 ч.
Одновременно автобус и катер первый раз окажутся в пункте А через целое число поездок, поэтому искомое время есть наименьшее общее кратное чисел 48 и 20 и равно 240 мин, т. е. 4 ч.
Этот материал взят со страницы решения задач с примерами по всем темам предмета математика:
Возможно вам будут полезны эти страницы:

