Оглавление:
Симметрические системы
Будем рассматривать системы вида
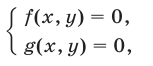
где 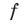 и
и 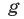 — многочлены, которые не изменяются при замене
— многочлены, которые не изменяются при замене 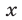 на
на 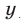 , а
, а 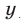 на
на 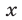 . Такие системы называются симметрическими. Простейшей системой этого типа является система
. Такие системы называются симметрическими. Простейшей системой этого типа является система
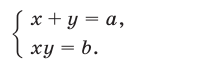
Используя теорему Виета, можно доказать, что система (1) и квадратное уравнение
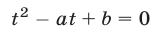
связаны следующим образом: если 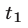 и
и 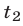 — корни квадратного уравнения (2), то система (1) имеет решения
— корни квадратного уравнения (2), то система (1) имеет решения 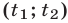 и
и 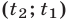 и не имеет других решений. Обратно, если
и не имеет других решений. Обратно, если 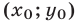 — решение системы (1), то
— решение системы (1), то 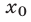 и
и 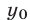 — корни уравнения (2).
— корни уравнения (2).
Например, система
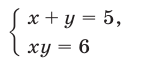
имеет два решения 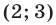 и
и 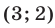 , так как уравнение
, так как уравнение 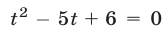 имеет два корня
имеет два корня 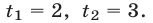
Многочлены 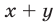 и
и 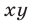 в левых частях уравнений системы (1) являются простейшими симметрическими многочленами, а любой симметрический многочлен от
в левых частях уравнений системы (1) являются простейшими симметрическими многочленами, а любой симметрический многочлен от 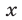 и
и 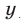 можно представить в виде многочлена от
можно представить в виде многочлена от 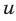 и
и 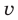 , где
, где 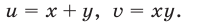
При решении симметрических систем часто приходится выражать через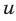 и
и 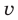 многочлены вида
многочлены вида
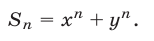
Суммы 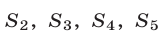 выражаются через
выражаются через 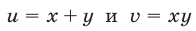 следующим образом:
следующим образом:
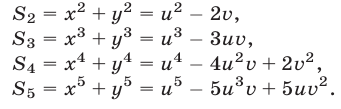
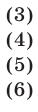
Формулы (3)-(6) можно легко получить самостоятельно. Докажем формулу
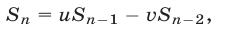
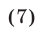
позволяющую последовательно выразить через 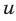 и
и 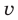 суммы
суммы 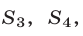
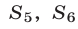 и т.д. Для этого заметим, что
и т.д. Для этого заметим, что
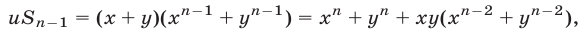
откуда и следует равенство (7).
Пример №174.
Решить систему уравнений
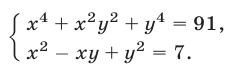
Решение:
Это — симметрическая система. Полагая 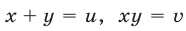 и используя формулы (3), (5), запишем ее в виде
и используя формулы (3), (5), запишем ее в виде
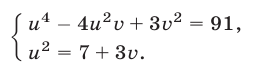
Исключая из этой системы 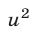 , получаем
, получаем
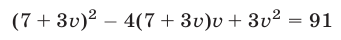
или 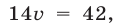 откуда
откуда 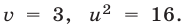 Следовательно, исходная система равносильна совокупности двух систем
Следовательно, исходная система равносильна совокупности двух систем
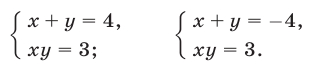
Ответ. 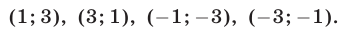
Пример №175.
Решить систему уравнений
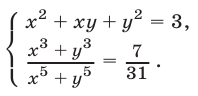
Решение:
Воспользуемся формулами (3), (4), (6). Тогда система примет вид
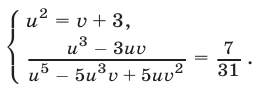
Так как 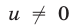 (при
(при 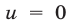 второе уравнение системы теряет смысл), то, разделив числитель и знаменатель дроби на
второе уравнение системы теряет смысл), то, разделив числитель и знаменатель дроби на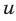 и исключая из системы
и исключая из системы 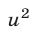 , преобразуем второе уравнение к виду
, преобразуем второе уравнение к виду 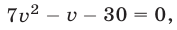 откуда
откуда 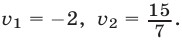
Если 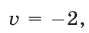 то
то 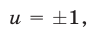 а если
а если 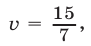 то
то 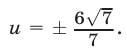 Поэтому исходная система равносильна совокупности следующих четырех систем:
Поэтому исходная система равносильна совокупности следующих четырех систем:
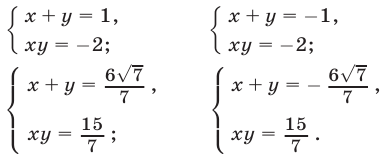
Первая система имеет решения 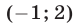 и
и 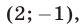 вторая — решения
вторая — решения 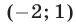 и
и 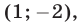 третья и четвертая системы не имеют действительных решений.
третья и четвертая системы не имеют действительных решений.
Ответ. 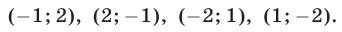
Замечание. К системе симметрических уравнений иногда бывает удобно свести иррациональное уравнение. Например, при решении уравнения
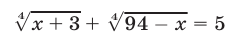
ввести вспомогательные неизвестные 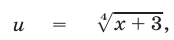
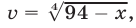 и мы получим систему
и мы получим систему
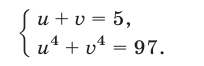
Этот материал взят со страницы решения задач с примерами по всем темам предмета математика:
Возможно вам будут полезны эти страницы:

