Оглавление:
Тригонометрические уравнения различных видов
Примеры с решениями
Пример №153.
Решить уравнение
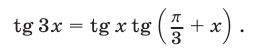
Решение:
Воспользуемся формулой
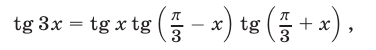
полученной в §4 (см. замечание к примеру 9). Тогда исходное уравнение можно записать в виде
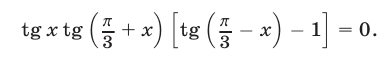
Ответ. 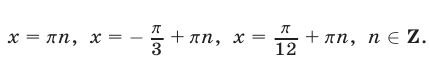
Пример №154.
Решить уравнение 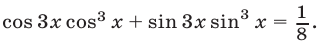
Решение:
Используя тождество
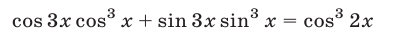
(см. §4, пример 5), запишем уравнение в виде 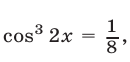 откуда находим
откуда находим 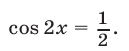
Ответ. 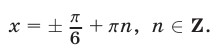
Пример №155.
Решить уравнение 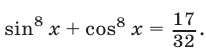
Решение:
Используя тождество
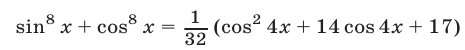
(см. §4, пример 4, в), запишем данное уравнение в виде
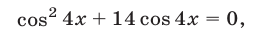
откуда находим 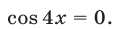
Ответ. 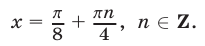
Пример №156.
Решить уравнение
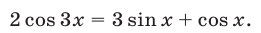
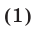
Решение:
Первый способ. Запишем уравнение (1) в виде
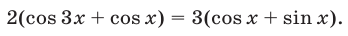
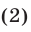
Так как 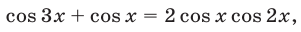
 то уравнение (2) равносильно совокупности уравнений
то уравнение (2) равносильно совокупности уравнений
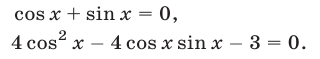
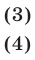
Уравнение (3) имеет корни 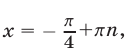 а уравнение (4) сводится к однородному
а уравнение (4) сводится к однородному
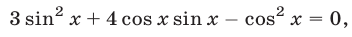
которое равносильно уравнению
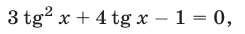
откуда 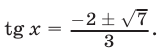
Ответ. 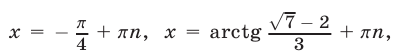
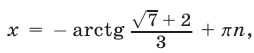
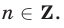
Второй способ. Уравнение (1) можно последовательно преобразовать так:
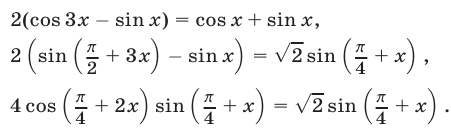
Дальнейшие действия очевидны.
Третий способ. Используя формулу 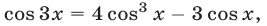 последовательно преобразуем уравнение (1):
последовательно преобразуем уравнение (1):
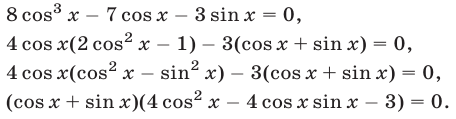
Снова убеждаемся в том, что уравнение (1) равносильно совокупности уравнений (3), (4).
Пример №157.
Найти все значения 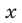 из интервала
из интервала 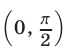 удовлетворяющие уравнению
удовлетворяющие уравнению
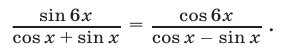
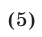
Решение:
Так как 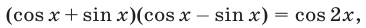 то ОДЗ уравнения (5) определяется условием
то ОДЗ уравнения (5) определяется условием 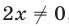 , т. е.
, т. е.
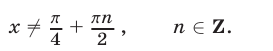
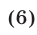
При выполнении условия (6) уравнение (5) равносильно каждому из уравнений:
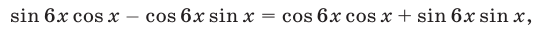
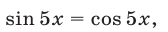
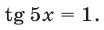
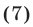
Уравнение (7) имеет корни
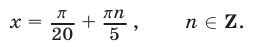
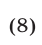
Неравенству 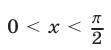 и условию (6) могут удовлетворять лишь те значения
и условию (6) могут удовлетворять лишь те значения 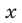 , определяемые формулой (8), которые соответствуют значениям
, определяемые формулой (8), которые соответствуют значениям 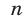 , равным
, равным 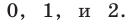 Придавая
Придавая 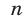 эти значения, по формуле (8) находим числа
эти значения, по формуле (8) находим числа 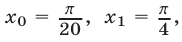 из которых лишь
из которых лишь 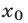 и
и 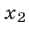 удовлетворяют условию (6).
удовлетворяют условию (6).
Ответ. 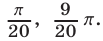
Пример №159.
Решить уравнение
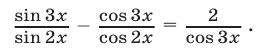
Решение:
Исходное уравнение равносильно уравнению
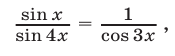
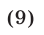
а допустимые значения х для уравнения (9) определяются условиями
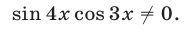
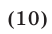
При выполнении условия (10) уравнение
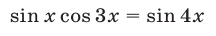
является следствием уравнения (9) и равносильно уравнению
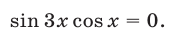
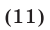
Корнями уравнения (9) являются все те и только те корни уравнения (11), которые удовлетворяют условиям (10).
Так как 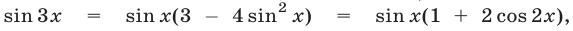 а
а 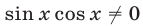 силу (10), то из (11) следует, что
силу (10), то из (11) следует, что
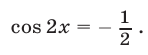
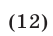
Корни уравнения (12) удовлетворяют условиям (10) и являются корнями исходного уравнения.
Ответ. 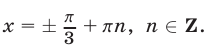
Пример №160.
Решить уравнение
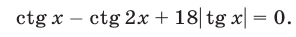
Решение:
Пусть 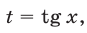 тогда
тогда 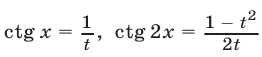 и уравнение (13) примет вид
и уравнение (13) примет вид
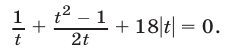
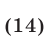
1) Если 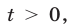 то из (14) следует, что
то из (14) следует, что 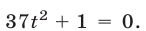 Это уравнение не имеет корней. Поэтому уравнение (13) не имеет корней в случае, когда
Это уравнение не имеет корней. Поэтому уравнение (13) не имеет корней в случае, когда 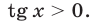
2) Если 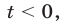 то из уравнения (14) следует, что
то из уравнения (14) следует, что 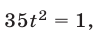 откуда
откуда
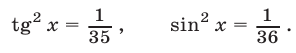
Если 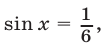 то либо
то либо 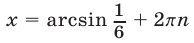 , значит,
, значит, 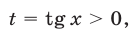 либо
либо 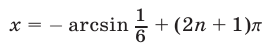 , значит,
, значит, 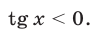 Если
Если 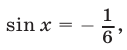 то либо
то либо 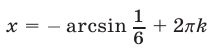 и, значит,
и, значит, 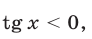 либо
либо 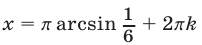 и, значит,
и, значит, 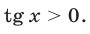
Ответ. 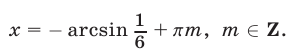
Пример №161.
Решить уравнение
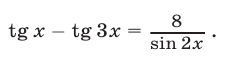
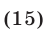
Решение:
Допустимые значения 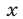 определяются условиями
определяются условиями
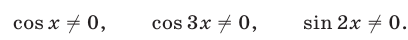
Преобразуем уравнение (15):
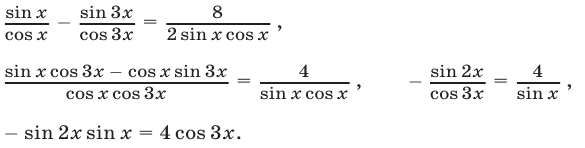
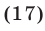
Уравнение (17) является следствием уравнения (15), а при выполнении условий (16) оно равносильно уравнению (15). Применив формулу 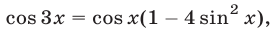 запишем уравнение (17) в виде
запишем уравнение (17) в виде
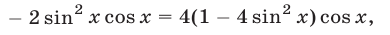
или
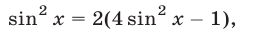
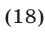
так как 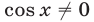 в силу условий (16).
в силу условий (16).
Используя формулу 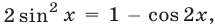 преобразуем уравнение (18) к виду
преобразуем уравнение (18) к виду 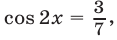 откуда
откуда 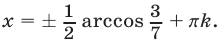 Найденные значения
Найденные значения 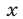 удовлетворяют условиям (16) и являются корнями уравнения (15).
удовлетворяют условиям (16) и являются корнями уравнения (15).
Ответ. 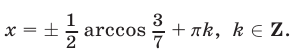
Пример №162.
Решить уравнение
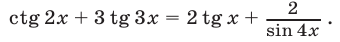
Решение:
Допустимые значения 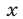 определяются условиями
определяются условиями

Используя равенства
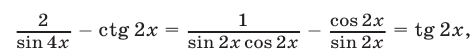
запишем уравнение (19) в виде
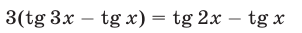
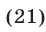
или
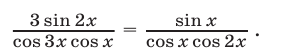
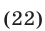
При выполнении условий (20) уравнение (22) равносильно каждому из следующих уравнений:
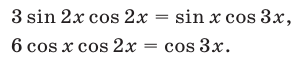
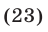
Применив формулу 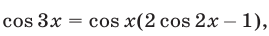 запишем уравнение (23) в виде
запишем уравнение (23) в виде
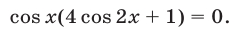
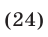
Так как 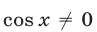 в силу условий (20), то из (24) следует, что
в силу условий (20), то из (24) следует, что 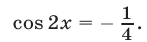
Ответ. 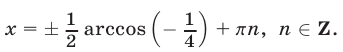
Замечание. Выразив 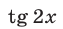 и
и 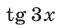 через
через 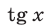 , преобразуем уравнение (21) к виду
, преобразуем уравнение (21) к виду 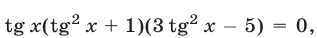 откуда следует, что
откуда следует, что 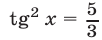 или
или 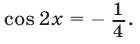
Пример №163.
Решить уравнение
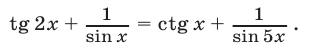
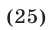
Решение:
Допустимые значения 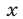 определяются условиями
определяются условиями

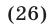
так как 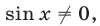 если
если 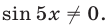
Считая условия (26) выполненными, преобразуем последовательно уравнение (25):
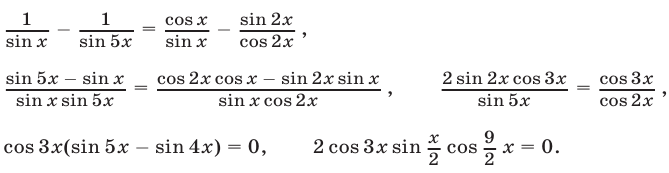
Если 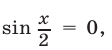 то
то 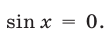 Поэтому решение сводится к нахождению тех корней уравнений
Поэтому решение сводится к нахождению тех корней уравнений 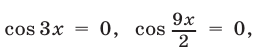 которые удовлетворяют условиям (26).
которые удовлетворяют условиям (26).
Уравнение 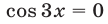 имеет корни
имеет корни
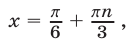
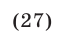
а уравнение 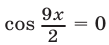 имеет корни
имеет корни
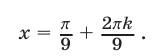
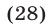
Серия корней (27) удовлетворяет условиям (26). Для серии корней (28) условие 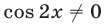 выполняется, а равенство
выполняется, а равенство
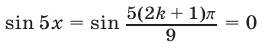
является верным тогда и только тогда, когда 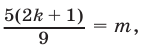 где
где 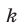 ,
, 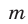 — целые числа. Так как числа 5 и 9 взаимно просты, то число
— целые числа. Так как числа 5 и 9 взаимно просты, то число 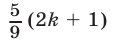 является целым в том и только в том случае, когда
является целым в том и только в том случае, когда 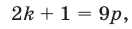 где
где 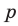 — целое число.
— целое число.
Ответ. 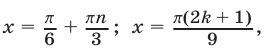
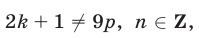
Этот материал взят со страницы решения задач с примерами по всем темам предмета математика:
Возможно вам будут полезны эти страницы:

