Оглавление:
Разложение многочлена на множители
а) Если х = а — корень многочлена 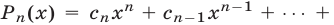
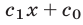 где
где 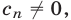 т.е.
т.е. 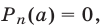 то
то 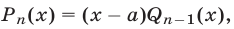 где
где 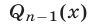 — многочлен степени
— многочлен степени 
б) Если 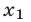 и
и 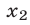 — корни квадратного трехчлена
— корни квадратного трехчлена 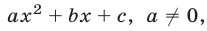 то
то
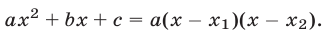
Пример №13.
Вычислить сумму
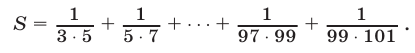
Решение:
В этой задаче речь идет не о приближенном значении суммы, которое можно получить с помощью таблиц или других вычислительных средств, а о точном значении суммы, т.е. о записи S в виде отношения двух натуральных чисел.
Ключевой момент решения задачи — представление дроби 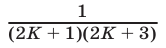 в виде разности двух дробей, т.е. использование
в виде разности двух дробей, т.е. использование
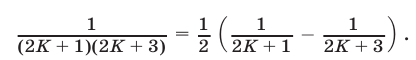
Применяя это равенство, получаем
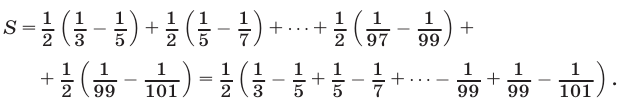
Все слагаемые полученной суммы, за исключением первого и последнего, попарно взаимно уничтожаются и поэтому
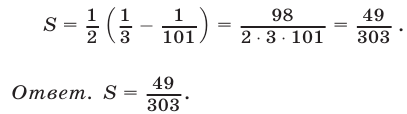
Замечание. Метод, использованный в этой задаче, можно применить для вычисления суммы
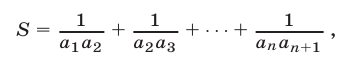
где 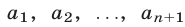 — последовательные отличные от нуля члены арифметической прогрессии.
— последовательные отличные от нуля члены арифметической прогрессии.
Эта ссылка возможно вам будет полезна:
Пример №14.
Доказать, что равенство
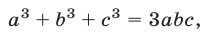
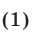
где а, b, с — положительные числа, является верным тогда и только тогда, когда
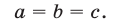
Решение:
Воспользуемся равенством
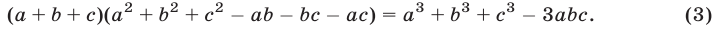
Это равенство справедливо для любых чисел а, b, с, в чем нетрудно убедиться, произведя действия в левой части (3).
Если а, b, с— положительные числа, то из (1) и (3) следует, что должно выполняться равенство
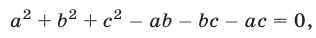 ,
, 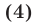
которое можно записать в виде
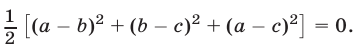
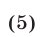
Но равенство (5) для действительных чисел a, b и с выполняется (является верным) только в том случае, когда выполняются условия (2).
Замечание. Из (3)-(5) следует, что для любых чисел а, b, с справедливо равенство.
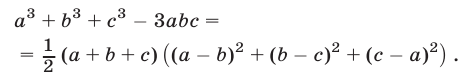
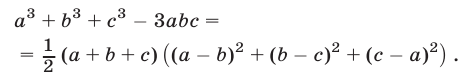
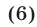
Если а, b, с — неотрицательные числа, то правая часть (6) — неотрицательное число, и поэтому
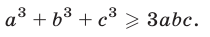
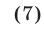
Полагая в 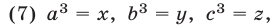 получаем неравенство
получаем неравенство 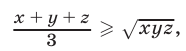
связывающее среднее арифметическое и среднее геометрическое неотрицательных чисел х, у, z.
Пример №15.
Доказать, что если три действительных числа а, b, с удовлетворяют условию
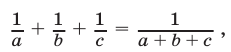
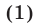
то по крайней мере два из этих чисел равны по абсолютной величине и противоположны по знаку, т.е. выполняется хотя бы одно из условий
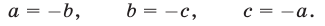
Решение:
Умножив обе части равенства (1) на 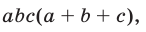 приведем его к виду
приведем его к виду
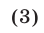
Раскрыв скобки в левой части (3), получим
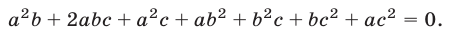
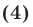
Разложим левую часть S равенства (4) на множители:
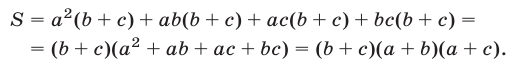
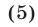
Из (4) и (5) следует, что
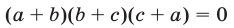
и поэтому выполняется хотя бы одно из условий (2).
Замечание. Полученный результат позволяет сформулировать следующее утверждение: если действительные числа а, b, с связаны условием (1), то при любом натуральном k справедливо равенство
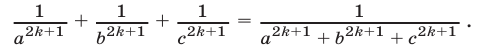
Пример №16.
Сократить дробь
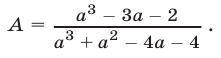
Решение:
Так как числитель 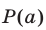 и знаменатель
и знаменатель 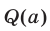 дроби
дроби 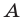 обращаются в нуль при
обращаются в нуль при 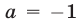 , то многочлены
, то многочлены 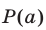 и
и 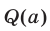 делятся на
делятся на 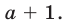 Разложим эти многочлены на множители. Получим
Разложим эти многочлены на множители. Получим
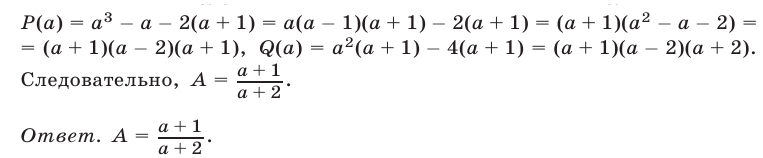
Этот материал взят со страницы решения задач с примерами по всем темам предмета математика:
Возможно вам будут полезны эти страницы:
| Рациональные числа примеры с решением |
| Множество действительных чисел примеры с решением |
| Производные пропорции примеры с решением |
| Действия с корнями (радикалами) примеры с решением |

