Оглавление:
Множество действительных чисел
а) Иррациональное число — бесконечная десятичная непериодическая дробь. Рациональные числа, представимые бесконечными периодическими десятичными дробями, и иррациональные числа образуют множество действительных чисел R.
б) Арифметические действия и правила сравнения для действительных чисел определяются так, что свойства этих действий, а также свойства равенств и неравенств оказываются такими же, как и для рациональных чисел. Правила сравнения и операции над действительными числами подробно изучаются в курсе высшей математики.
в) Модулем действительного числа а называется неотрицательное число (обозначается |а|) такое, что

Возведение в целую степень
а) Определение степени.
Если а — действительное число 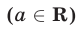 , n— натуральное число
, n— натуральное число 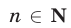 , то
, то
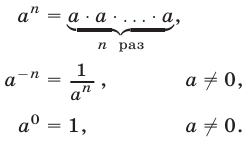
б) Свойства степени.
Если 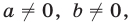 m и n — целые числа
m и n — целые числа 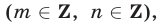 то
то
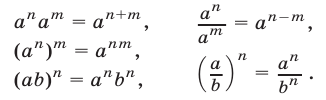
в) Степень суммы и разности.
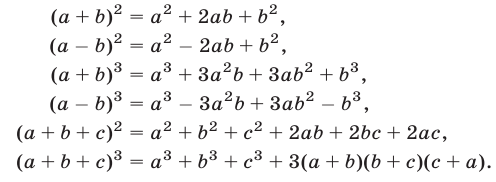
г) Разность и сумма степеней.
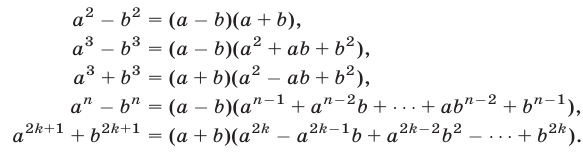
Пример №11.
Упростить выражение
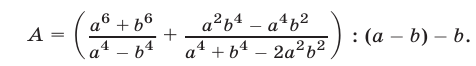
Решение:
Используя формулы для суммы кубов, разности квадратов и квадрата разности, получаем 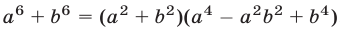 ,
, 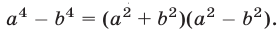
Сократив числитель и знаменатель первой дроби на 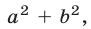 а второй дроби — на
а второй дроби — на  , находим
, находим
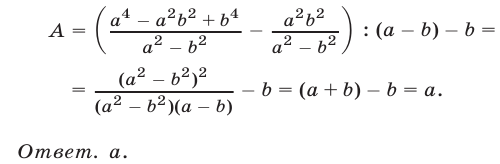
Пример №12.
Упростить выражение
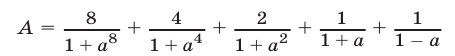
и найти его значение при 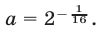
Решение:
Сумма двух последних дробей равна 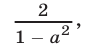 а сумма трех последних дробей равна
а сумма трех последних дробей равна 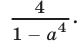 Следовательно,
Следовательно, 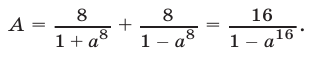 Если
Если 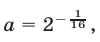 то
то 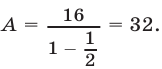
Ответ. 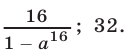
Этот материал взят со страницы решения задач с примерами по всем темам предмета математика:
Возможно вам будут полезны эти страницы:
| Метод математической индукции примеры с решением |
| Рациональные числа примеры с решением |
| Разложение многочлена на множители примеры с решением |
| Производные пропорции примеры с решением |

