Оглавление:
Прямые и обратные теоремы. Необходимые и достаточные условия.
а) Формулировка каждой теоремы содержит условие теоремы и заключение. Поменяв местами в формулировке некоторой теоремы условие и заключение, получим формулировку теоремы, обратной данной.
б) Пусть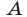 
— некоторое высказывание, т. е. утверждение, о котором имеет смысл говорить, что оно истинно или ложно. Тогда всякое высказывание 
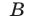, из которого следует 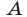, называется достаточным условием для 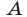, а всякое высказывание 
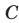, которое следует из 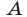, называется необходимым условием для 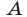. В этих случаях пишут: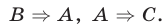 
в) Если высказывания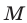 
и 
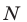таковы, что каждое из них следует из другого 
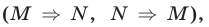то говорят, что каждое из этих высказываний является необходимым и достаточным условием другого, и пишут 
. Тот факт, что , выражают также следующими формулировками:
— для справедливости 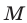необходимо и достаточно, чтобы имело место ;
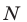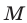— справедливо тогда и только тогда, когда выполняется ;
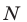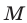— имеет место в том и только в том случае, если справедливо .
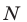Пример №1.
Сформулировать и доказать теорему, обратную теореме Пифагора.
Решение:
Условие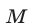 
теоремы Пифагора можно записать в виде следующего высказывания:
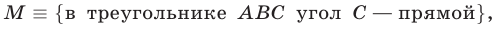
а заключение 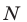этой теоремы формулируется так:
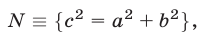
где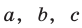 
— стороны, лежащие против углов 
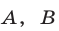и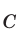 
соответственно.
Справедлива также теорема, обратная теореме Пифагора: если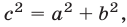 
то угол 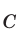— прямой.
Для доказательства этой теоремы можно воспользоваться либо теоремой косинусов, либо третьим признаком равенства треугольников (по трем сторонам).
Пример №2.
Выяснить, какое из утверждений 
и 
следует из другого, используя символы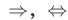 
:
Решение:
1) Здесь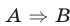 
, но из 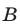не следует .
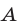2) В этом случае 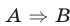и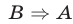 
, т. е. 
.
Этот материал взят со страницы решения задач с примерами по всем темам предмета математика:
Возможно вам будут полезны эти страницы:
