Оглавление:
Множество чисел, каждое из которых снабжено своим номером, называется числовой последовательностью. Элементы этого числового множества называются членами последовательности. Числовая последовательность обычно обозначается малой латинской буквой с номером; например 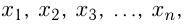 Формула, позволяющая вычислить любой член последовательности по его номеру, называется формулой общего члена последовательности. Последовательность может быть конечной и бесконечной. Например, последовательность цифр конечна и состоит из
Формула, позволяющая вычислить любой член последовательности по его номеру, называется формулой общего члена последовательности. Последовательность может быть конечной и бесконечной. Например, последовательность цифр конечна и состоит из 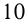 цифр:
цифр: 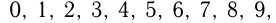 последовательность натуральных чисел бесконечна.
последовательность натуральных чисел бесконечна.
Множество чисел, каждое из которых снабжено своим номером, называется числовой последовательностью. Элементы этого числового множества называются членами последовательности. Числовая последовательность обычно обозначается малой латинской буквой с номером; например
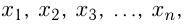
Формула, позволяющая вычислить любой член последовательности по его номеру, называется формулой общего члена последовательности. Последовательность может быть конечной и бесконечной. Например, последовательность цифр конечна и состоит из
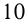
цифр:
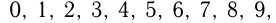
последовательность натуральных чисел бесконечна.
Последовательность называется возрастающей, если для всех 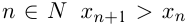 , и убывающей, если для всех
, и убывающей, если для всех 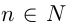
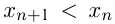 . Соответственно, неубывающая и невозрастающая последовательности определяются так: при всех
. Соответственно, неубывающая и невозрастающая последовательности определяются так: при всех 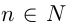
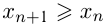 либо
либо 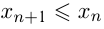 .
.
Задача №135
Доказать, что последовательность, заданная формулой общего члена 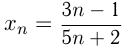 , — возрастающая.
, — возрастающая.
Решение:
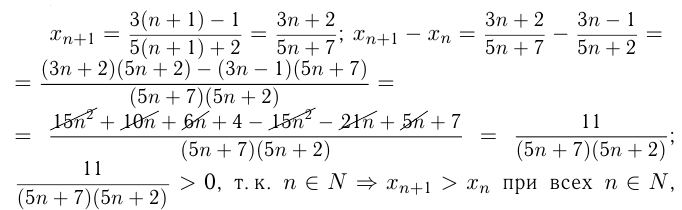
и прогрессия возрастающая.
Если последовательность чисел подчиняется закону: 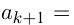
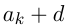 , где
, где 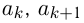 — два соседних члена последовательности, a
— два соседних члена последовательности, a 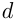 — разность между ними, постоянная для всех таких соседних чисел, то эта последовательность называется арифметической прогрессией,
— разность между ними, постоянная для всех таких соседних чисел, то эта последовательность называется арифметической прогрессией,
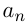 —
— 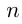 -й член арифметической прогрессии;
-й член арифметической прогрессии;
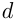 — разность арифметической прогрессии;
— разность арифметической прогрессии;
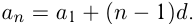
Сумма 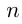 членов арифметической прогрессии определяется по формулам:
членов арифметической прогрессии определяется по формулам:
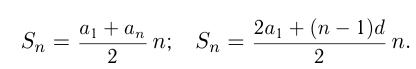
Признак арифметической прогрессии формулируется так: каждый член арифметической прогрессии, начиная со 2-го, есть среднее арифметическое соседних с ним чисел:
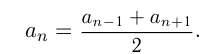
Если последовательность чисел подчиняется закону: 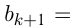
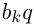 , где
, где 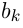 и
и 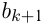 — два соседних члена последовательности, а
— два соседних члена последовательности, а 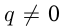 — постоянное для этой последовательности число, то это геометрическая прогрессия. Если
— постоянное для этой последовательности число, то это геометрическая прогрессия. Если 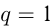
, то все члены прогрессии равны между собой. В этом случае прогрессия является постоянной последовательностью.
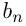 —
— 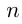 -й член геометрической прогрессии;
-й член геометрической прогрессии; 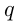 — знаменатель геометрической прогрессии;
— знаменатель геометрической прогрессии;
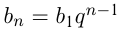
Сумма 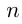 членов геометрической прогрессии определяется по формулам:
членов геометрической прогрессии определяется по формулам:
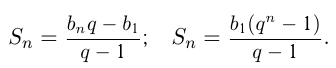
Если 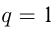 , то
, то 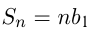 .
.
Геометрическая прогрессия, у которой 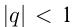 , называется бесконечно убывающей, а ее сумма определяется по формуле:
, называется бесконечно убывающей, а ее сумма определяется по формуле:
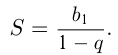
Признак геометрической прогрессии имеет формулировку: каждый член геометрической прогрессии, начиная со 2-го, есть среднее геометрическое соседних с ним чисел:
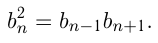
Задачи на прогрессии
Задача №136
В арифметической прогрессии 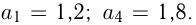 Найти
Найти 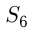 .
.
Решение:
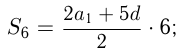 нужно найти
нужно найти 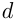 .
.
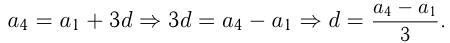
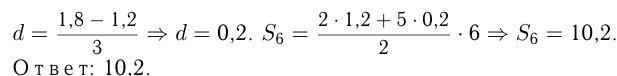
Задача №137
Найти сумму всех двузначных положительных чисел.
Решение:
Эти числа образуют арифметическую прогрессию, у которой 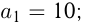
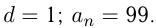
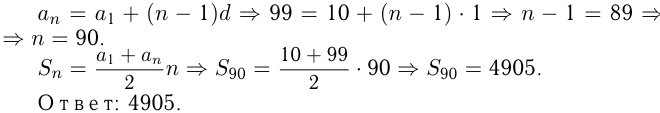
Задача №138
Сумма 4-го и 6-го членов арифметической прогрессии равна 14. Найти сумму первых девяти членов прогрессии.
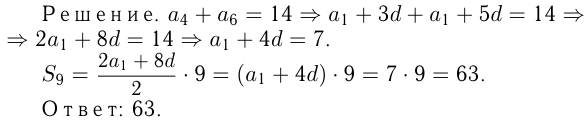
Задача №139
Знаменатель геометрической прогрессии равен —2, сумма ее первых пяти членов равна 5,5. Найти пятый член прогрессии.
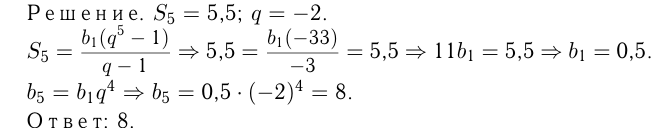
Задача №140
В геометрической прогрессии 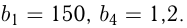 Найти
Найти 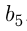 .
.
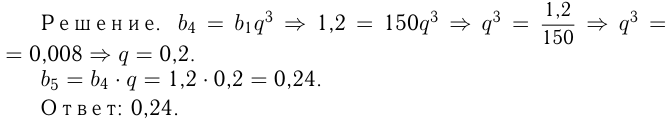
Задача №141
Найти сумму всех трехзначных натуральных чисел, которые при делении на 5 дают остаток 1.
Решение:
Все такие числа образуют арифметическую прогрессию, в которой 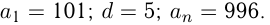
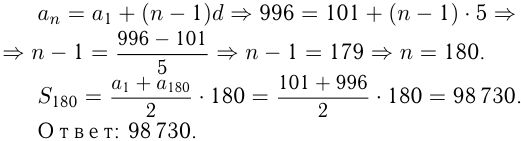
Задача №142
Сколько имеется двузначных натуральных чисел, кратных 6?
Решение:
1-е двузначное число, кратное 6, равно 12, 2-е число — 18, 3-е — 24 и т.д., т.е. такие числа образуют арифметическую прогрессию: 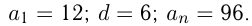
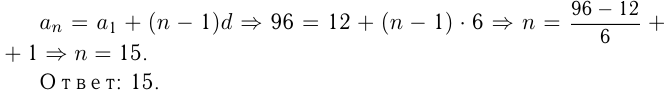
Задача №143
В геометрической прогрессии 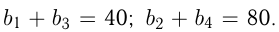 Найти
Найти 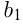 и
и 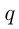 .
.
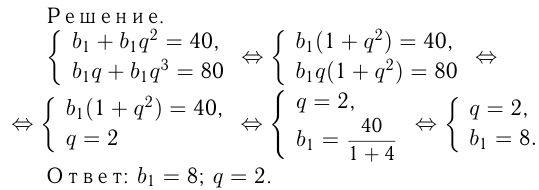
Задача №144
Между числами 1 и 256 вставить 3 числа так, чтобы все пять чисел составляли геометрическую прогрессию.
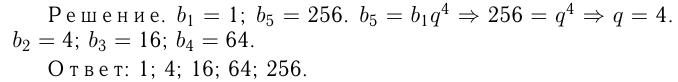
Задача №145
Сумма бесконечно убывающей геометрической прогрессии равна 32, а сумма ее первых пяти членов равна 31. Найти 1-й член прогрессии.
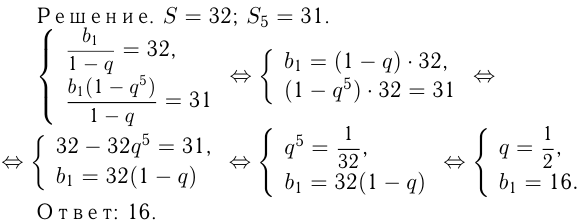
Задача №146
Сумма 3-х положительных чисел, составляющих арифметическую прогрессию, равна 15. Если ко 2-му из них прибавить 1, к 3-му 5, а 1-е оставить без изменения, то получится геометрическая прогрессия. Найти исходные числа.
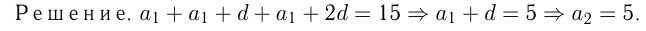
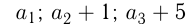 геометрическая прогрессия со знаменателем
геометрическая прогрессия со знаменателем 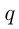 .
.
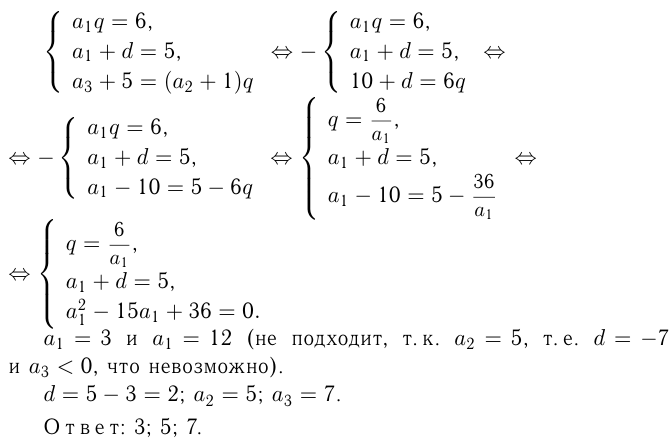
Задача №147
Найти первый член и разность арифметической прогрессии, если сумма ее первых 3-х членов равна 27, а сумма их квадратов равна 275.
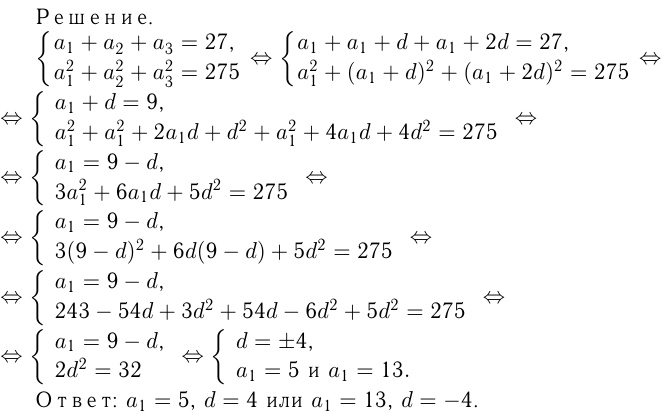
Задача №148
Найти первый член и знаменатель геометрической прогрессии 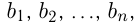 если известно, что
если известно, что 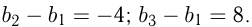
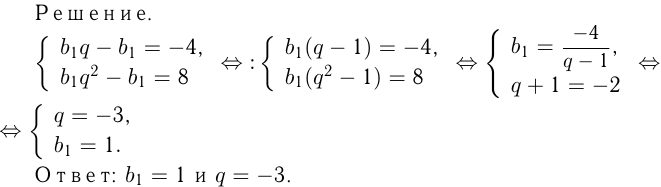
Задача №149
Найти 4 целых числа 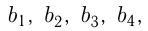 если известно, что числа
если известно, что числа 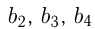 образуют геометрическую прогрессию, а
образуют геометрическую прогрессию, а 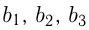 образуют арифметическую прогрессию и
образуют арифметическую прогрессию и 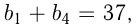
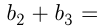
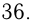
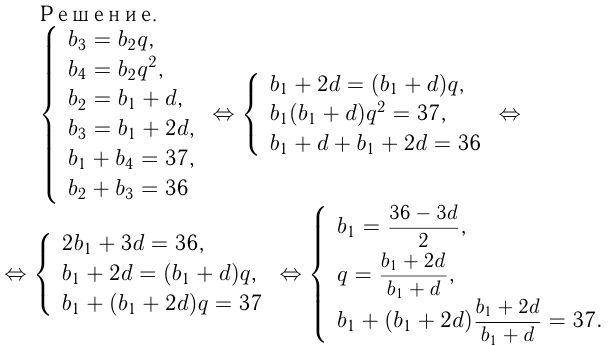
Преобразуем 3-е уравнение:
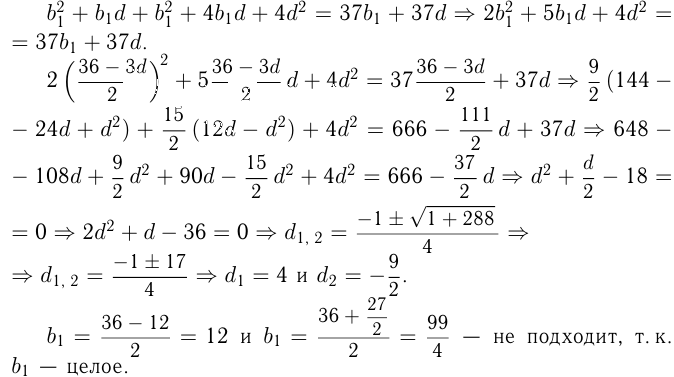
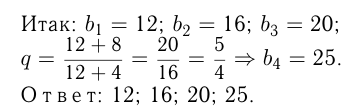
Задача №150
Известно, что при любом 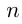 сумма
сумма 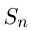 членов некоторой арифметической прогрессии выражается формулой
членов некоторой арифметической прогрессии выражается формулой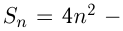
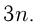 Найти четыре первых члена этой прогрессии.
Найти четыре первых члена этой прогрессии.
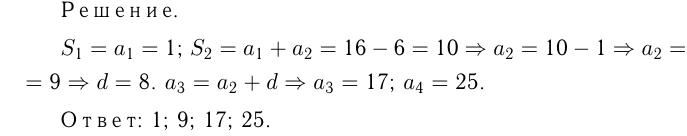
Задача №151
Найти 1-й и 5-й члены геометрической прогрессии, если известно, что 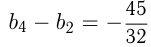 и
и 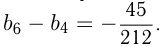
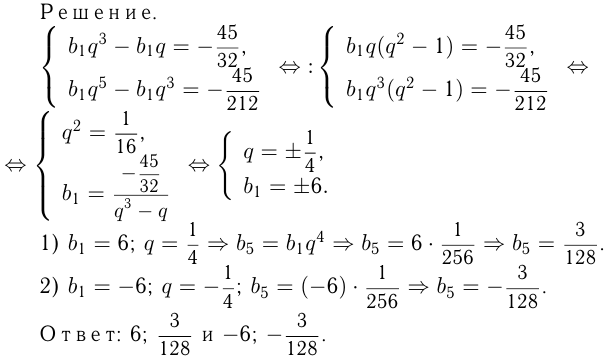
Задача №152
Найти 3 числа, образующие геометрическую прогрессию, если известно, что их произведение равно 64, а их среднее арифметическое равно 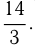
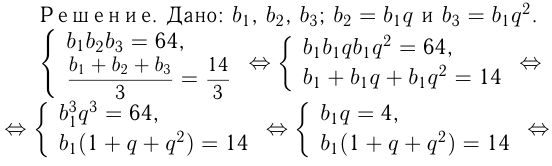
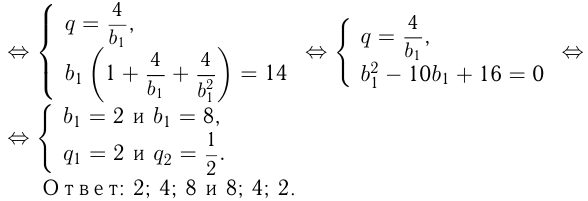
Задача №153
Найти четыре первых члена арифметической прогрессии, у которой сумма любого числа членов равна утроенному квадрату этого числа.
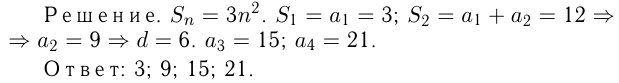
Задача №154
Три числа, из которых третье равно 12, образуют геометрическую прогрессию. Если вместо 12 взять 9, то три числа составят арифметическую прогрессию. Найти эти числа.
Решение:
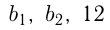 — геометрическая прогрессия;
— геометрическая прогрессия; 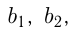
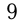 — арифметическая прогрессия.
— арифметическая прогрессия.
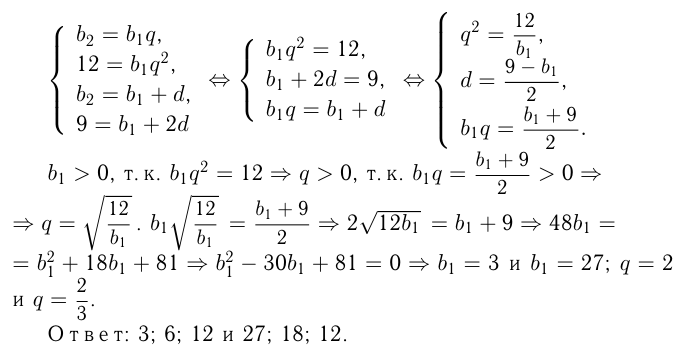
Задача №155
Решить уравнение
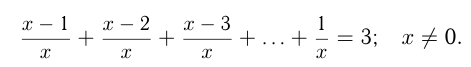
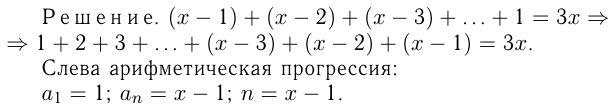
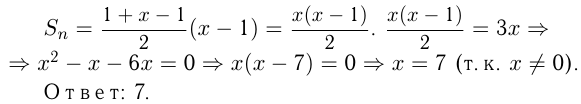
Задача №156
Сумма 3-х чисел равна 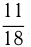 а сумма обратных им чисел, составляющих арифметическую прогрессию, равна
а сумма обратных им чисел, составляющих арифметическую прогрессию, равна 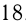 . Найти эти числа.
. Найти эти числа.
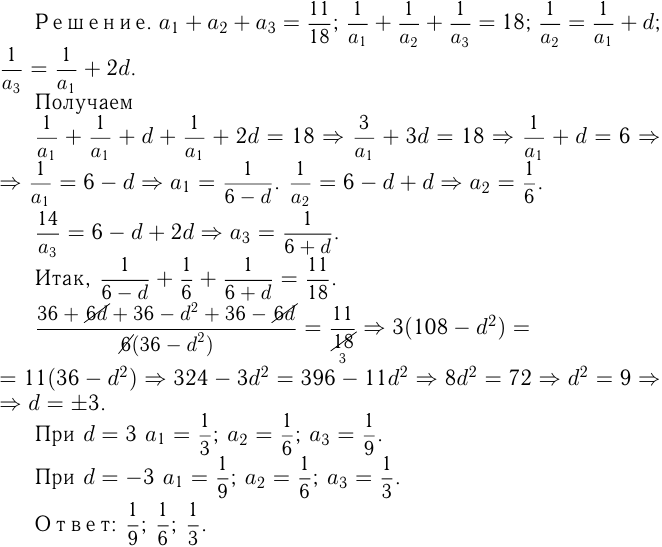
Задача №157
Найти сумму семи первых членов бесконечной геометрической прогрессии со знаменателем 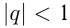 , если ее 2-й член равен
, если ее 2-й член равен 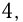 а отношение суммы квадратов членов к сумме членов равно
а отношение суммы квадратов членов к сумме членов равно 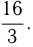
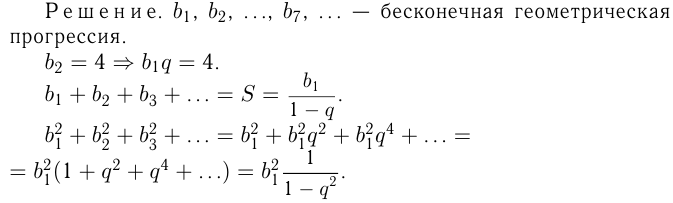
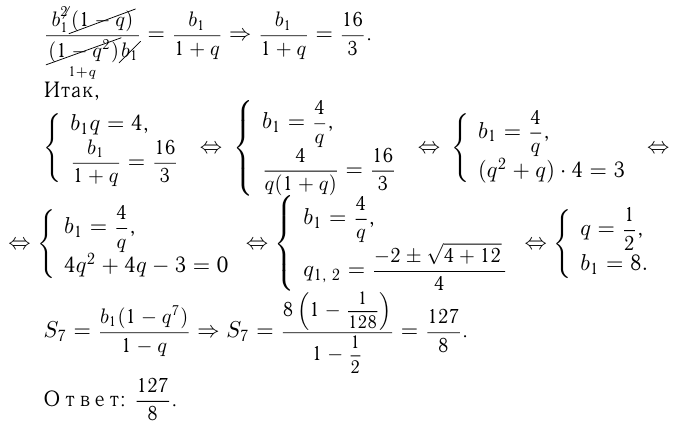
Задача №158
Даны арифметическая и геометрическая прогрессии. В арифметической прогрессии 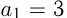 и
и 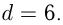 В геометрической прогрессии
В геометрической прогрессии 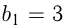 и
и 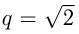 . Выяснить, что больше: сумма первых шести членов арифметической прогрессий или сумма первых восьми членов геометрической прогрессии?
. Выяснить, что больше: сумма первых шести членов арифметической прогрессий или сумма первых восьми членов геометрической прогрессии?
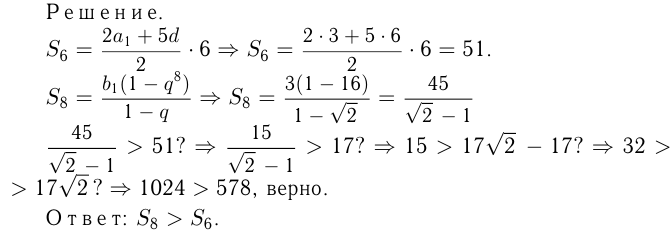
Задача №159
Магазин радиотоваров продал в 1-й рабочий день месяца 105 телевизоров. Каждый следующий рабочий день дневная продажа возрастала на 10 телевизоров, и месячный план — 4000 телевизоров — был выполнен досрочно, причем в целое число рабочих дней. После этого ежедневно продавалось на 13 телевизоров меньше, чем в день выполнения месячного плана. На сколько процентов был перевыполнен месячный план продажи телевизоров, если в месяце 26 рабочих дней?
Решение:
До выполнения плана продажа телевизоров происходила по закону арифметической прогрессии:

Этот материал взят со страницы решения задач по математике:
Возможно вам будут полезны эти страницы:
| Решение задач с целочисленными неизвестными по математике |
| Решение задач с помощью неравенств |
| Решение задач на функции по математике |
| Числа, числовые и алгебраические выражения |

