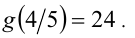Оглавление:
Функциональные уравнения
Функциональным уравнением называется уравнение, в котором в роли неизвестного выступает функция (или функции). В этом случае решением уравнения является любая функция, при подстановке которой в уравнение оно превращается в тождество. Решить функциональное уравнение значит найти множество всех его решений. Например, дифференциальные уравнения являются частными случаями функциональных уравнений.
Один из основных методов решения функциональных уравнений — метод замены переменной (метод подстановки) [7].
Пример №396.
Решить уравнение 
Решение:
Положив 
, возведём это равенство в квадрат:
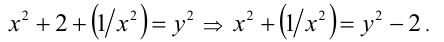
После перехода к новой переменной функциональное уравнение примет вид 
Следовательно, мы нашли функцию, это 
(какой буквой при этом обозначен аргумент функции — не играет большой роли, поэтому обозначим так, как привычно — буквой 
).
Однако необходимо сделать проверку найденного решения. Проверка нужна, в частности, по следующей причине: функция 
обладает тем свойством, что 
, поэтому остаётся вопрос — удовлетворяет ли найденная функция 
функциональному уравнению при 
Подставим функцию в исходное уравнение и проверим, действительно ли она удовлетворяет ему при всех 
Полученное равенство, очевидно, выполняется при всех действительных 
, поэтому функция 
будет единственным решением функционального уравнения.
Пример №397.
Найти функцию 
, при всех допустимых значениях удовлетворяющую уравнению
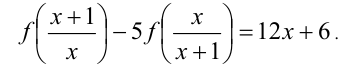
Решение:
ОДЗ: 
. Обозначим 
, отсюда 
, и исходное равенство примет вид
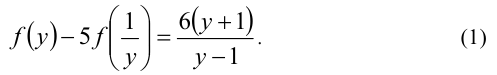
Если бы сделали замену 
, то получили бы равенство
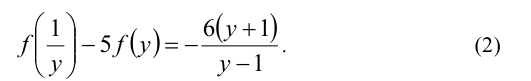
При этом оба равенства (1) и (2), согласно условию, выполняются при всех допустимых значениях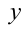 
. Решая систему уравнений (1) и (2) относительно 
и 
, находим 
. В ответе аргумент можно привычно обозначить буквой . Ответ: 
При решении функциональных уравнений нередко используется метод «от частного к общему». Рассмотрим примеры.
Пример №398.
Существует ли функция 
такая, что при любых действительных 
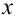и 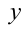выполняется равенство 
Решение:
Пользуясь тем, что 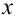и 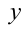— любые числа, положим в равенстве 
т.е. 
. Сделаем проверку, которая в данном случае обязательна (если при 
получается функция 
, которая при подстановке в функциональное уравнение превращает его в тождество, то это ещё не значит, что аналогичное положение будет и при 
). Получаем 
, но это равенство тождеством не является. Следовательно, такая функция не существует.
Пример №399.
Существуют ли функции и 
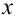такие, что при любых действительных и 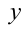выполняется равенство
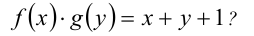
Решение:
Допустим, что такие функции и существуют, и попробуем их найти. Положим в функциональном уравнении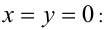 
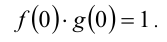
Теперь положим в нём 
:
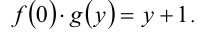
Наконец, положим в исходном равенстве 
:
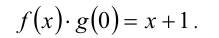
Перемножим два последних равенства:
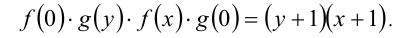
Но в этом равенстве 
, следовательно,
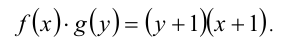
Сделаем проверку, подставив в исходное равенство:
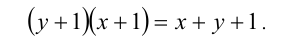
Очевидно, последнее равенство выполняется не при всех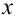 и 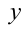. Пришли к противоречию. Следовательно, таких функций и не существует.
Пример №400.
Найти все функции , удовлетворяющие уравнению
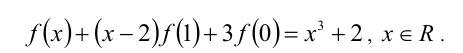
Решение:
Подставим в уравнение 
и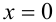 
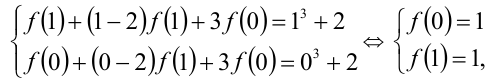
откуда получаем
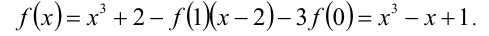
Проверкой убеждаемся, что найденная функция удовлетворяет уравнению. Ответ: 
В следующем примере требуется найти не саму функцию, удовлетворяющую заданному функциональному уравнению, а лишь её значение в некоторой точке. При решении необходимое значение последовательно выражается через другие (которые можно найти) значения этой функции.
Пример №401.
Числовая функция для всех действительных 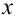и 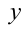удовлетворяет равенству
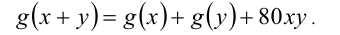
Найти 
, если 
.
Решение:
откуда
Пусть 
тогда
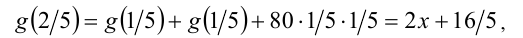
отсюда 
Записывая цепочку соотношений
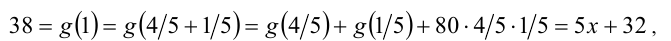
находим 
, следовательно, 
