Оглавление:
Уравнения вида 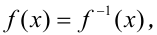 где
где 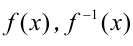 — взаимно обратные возрастающие функции
— взаимно обратные возрастающие функции
Теорема. Пусть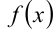 — монотонно возрастающая функция,
— монотонно возрастающая функция, 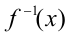 — её обратная функция. Тогда уравнение
— её обратная функция. Тогда уравнение 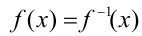 равносильно на ОДЗ уравнению
равносильно на ОДЗ уравнению 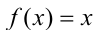 (или
(или 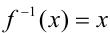 ).
).
Доказательство. Действительно, графики взаимно обратных функций 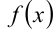 и
и 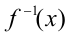 симметричны друг другу относительно прямой
симметричны друг другу относительно прямой 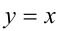 (см. рис.).
(см. рис.).
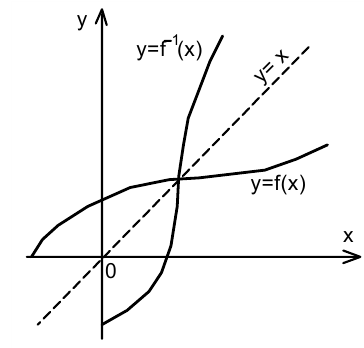
В случае возрастания функции 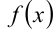 все точки пересечения этих графиков (при условии, что они существуют) лежат на этой прямой. Поэтому уравнение
все точки пересечения этих графиков (при условии, что они существуют) лежат на этой прямой. Поэтому уравнение
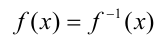
равносильно на ОДЗ каждому из уравнений 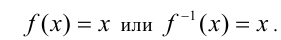 Заметим, что решение любого из последних уравнений может оказаться намного проще решения исходного.
Заметим, что решение любого из последних уравнений может оказаться намного проще решения исходного.
Следствие. Если, кроме того,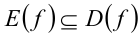 , то на множестве
, то на множестве 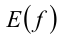 следующие уравнения являются равносильными:
следующие уравнения являются равносильными:
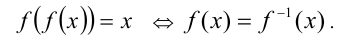
Для доказательства последнего утверждения достаточно применить к обеим частям второго из уравнений функцию 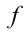 (применение к уравнению строго монотонной функции приводит к равносильному уравнению), и учесть, что
(применение к уравнению строго монотонной функции приводит к равносильному уравнению), и учесть, что
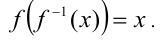
Пример №394.
Решить уравнение
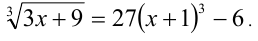
Решение:
Вначале приведём уравнение к виду
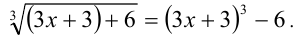
Введя переменную 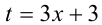 , придём к уравнению
, придём к уравнению

Покажем, что в левой и правой частях последнего уравнения находятся взаимно обратные функции. Действительно, рассмотрим функцию 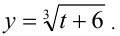 Это монотонно возрастающая функция, следовательно, она имеет обратную. Найдём её:
Это монотонно возрастающая функция, следовательно, она имеет обратную. Найдём её:
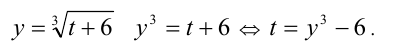
Поменяв местами обозначения переменных  , находим, что обратная функция имеет вид
, находим, что обратная функция имеет вид 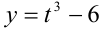 .
.
Далее, поскольку графики взаимно обратных возрастающих функций пересекаются в точках, лежащих на прямой 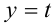 , то уравнение (1) равносильно уравнению
, то уравнение (1) равносильно уравнению
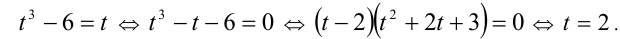
Таким образом, уравнение (1) имеет единственный корень 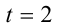 , которому соответствует
, которому соответствует 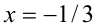 . Ответ:
. Ответ: 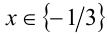 .
.
Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:
Эти страницы возможно вам будут полезны:

