Оглавление:
Уравнения и неравенства вида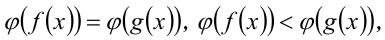 
где 
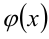строго монотонная функция. Применение к уравнению (неравенству) монотонной функции
Если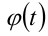 
— строго монотонная функция, то уравнение вида
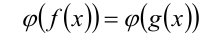
равносильно на ОДЗ уравнению
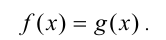
Простая же замена уравнения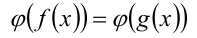 
уравнением 
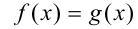приводит, вообще говоря, к следствию (так как снимаются требования, что значения функци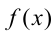й 
и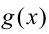 
должны принадлежать области определения 
.
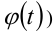Аналогично, если к обеим частям уравнения 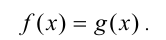применить функцию 
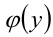определённую и строго монотонную на
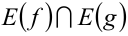то полученное уравнение 
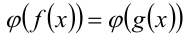будет (на ОДЗ исходного уравнения!) эквивалентно ему, т.е.
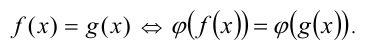
Пример №386.
Решить уравнение
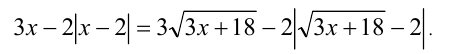
Решение:
Введём в рассмотрение функцию
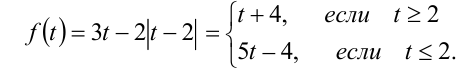
Функция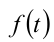 
возрастает на каждом из луче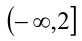й 
и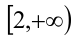 
. а поэтому возрастает на всей числовой прямой. Используя обозначение функции, уравнение можно переписать в виде
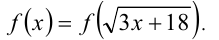
В силу строгой монотонности функции 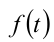, данное уравнение равносильно уравнению
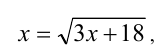
решая которое находим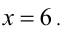 
Ответ: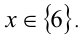 
Пример №387.
Решить систему уравнений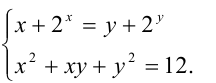 
Решение:
Первое уравнение в системе имеет вид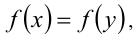 
где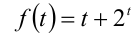 
монотонно возрастает при всех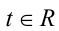 
и, следовательно, принимает каждое своё значение один раз. Откуда получаем 
.
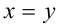Таким образом, исходная система равносильна системе
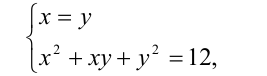
решая которую находим все решения задачи: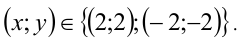 
Если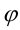 
— монотонно возрастающая (убывающая) функция, то неравенство
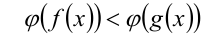
равносильно (на ОДЗ!) неравенству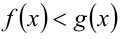 
(соответственно неравенству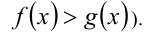 
В то же время, замена, например, неравенства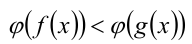 
неравенством 
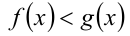приводит, вообще говоря, к следствию (так как снимаются требования, что значения функци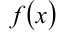й 
и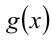 
должны принадлежать области определения функции ).
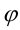Аналогично, если к обеим частям неравенства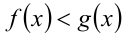 
(знак в неравенстве может быть любым) применить функцию 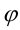, определённую и монотонно возрастающую (убывающую) на множестве 
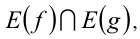то полученное неравенство 
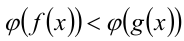(соответственно 
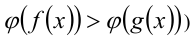будет эквивалентно исходному на его ОДЗ.
Пример №388.
Решить неравенство
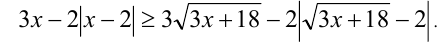
Решение:
Введём функцию
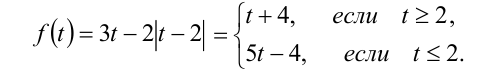
Функция 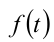определена и монотонно возрастает на каждом из луче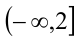й 
и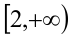 
, а поэтому возрастает на всей числовой прямой. Используя обозначение данной функции, перепишем исходное неравенство в виде
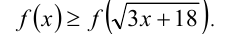
В силу строгого возрастания функции 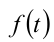данное неравенство равносильно неравенству
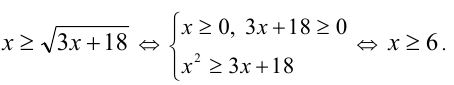
Пример №388.
Решить неравенство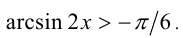 
Решение:
ОДЗ: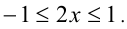 
Заметим, что обе части неравенства принимают значения в пределах от 
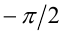до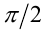 
, а на промежутке 
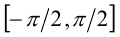функция 
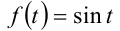монотонно возрастает. Поэтому, применяя к обеим частям неравенства операцию взятия синуса и сохраняя знак неравенства, получим новое неравенство, равносильное на ОДЗ исходному:
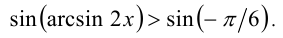
Упрощая, получим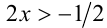 
, т.е. 
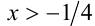. С учётом ОДЗ приходим к окончательному ответу. Ответ: 
.
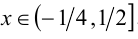Пример №389.
Что больше: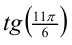 
или меньший корень квадратного трёхчлена 
?
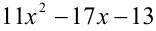Решение:
Упростим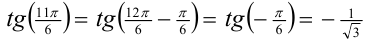 
Пусть 
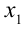и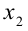 
— соответственно меньший и больший корни квадратного трёхчлена 
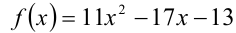. Если решать эту задачу напрямую, то надо найти меньший корень 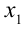, (он равен 
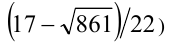и затем сравнить его с числом 
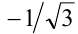. Но при этом возникают существенные вычислительные трудности (а пользоваться калькулятором на экзамене запрещено). Поэтому решим задачу иначе. Это можно сделать даже не находя в явном виде корня 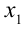. Итак, убедившись в положительности дискриминанта, что гарантирует наличие двух различных действительных корней, найдём по теореме Виета, что 
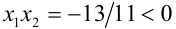. Следовательно, корни имеют разные знаки. Это означает, что меньший корень 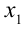— отрицательный. Заметим, что вершина параболы , 
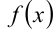имеет абсциссу 
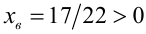, а старший коэффициент положителен. Тогда при 
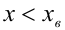и, в частности, при 
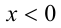функция 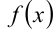монотонно убывает, а значит, большему значению аргумента отвечает меньшее значение функции. Поэтому задачу сравнения чисел 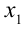, и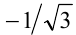 
можно свести к равносильной, но более простой задаче сравнения чисел 
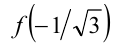и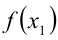 
. Поскольку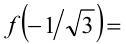 
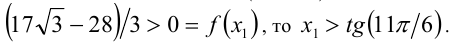Ответ: второе число больше.
Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:
Эти страницы возможно вам будут полезны:
