Оглавление:
Уравнения и неравенства вида 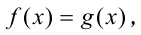
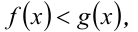 , где функции
, где функции 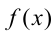 и
и 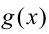 имеют разную монотонность
имеют разную монотонность
Уравнения вида 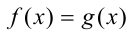 , где
, где 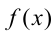 и
и 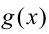 являются функциями разной монотонности (т.е. одна из них на ОДЗ возрастает, а другая, напротив, убывает), имеют не более одного решения. Если корень удаётся найти (подобрать), то это будет единственное решение. Отметим, что если вы используете данный метод для решения задачи, следует привести всю логическую цепочку обоснований (см. примеры ниже), включая обоснование монотонности функций (по определению или с помощью производной).
являются функциями разной монотонности (т.е. одна из них на ОДЗ возрастает, а другая, напротив, убывает), имеют не более одного решения. Если корень удаётся найти (подобрать), то это будет единственное решение. Отметим, что если вы используете данный метод для решения задачи, следует привести всю логическую цепочку обоснований (см. примеры ниже), включая обоснование монотонности функций (по определению или с помощью производной).
При этом если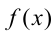 — возрастает,
— возрастает, 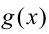 — убывает, а
— убывает, а 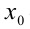 — корень уравнения, то
— корень уравнения, то 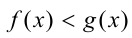 при
при 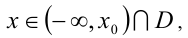 где
где 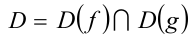 и
и 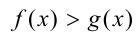 при
при 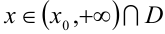 , т.е. данный подход можно применять и для решения соответствующих неравенств.
, т.е. данный подход можно применять и для решения соответствующих неравенств.
Метод применим и в том случае, когда в одной части уравнения стоит строго монотонная функция, а в другой — постоянная функция.
Пример №383.
Решить уравнение 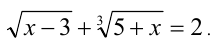
Решение:
Очевидно, что 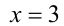 является решением. Покажем, что других корней нет. В самом деле, в левой части уравнения находится сумма двух монотонно возрастающих на ОДЗ уравнения функций
является решением. Покажем, что других корней нет. В самом деле, в левой части уравнения находится сумма двух монотонно возрастающих на ОДЗ уравнения функций
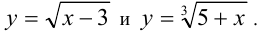
Докажем, например, что функция 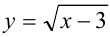 возрастает при
возрастает при 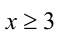 . По определению, функция
. По определению, функция 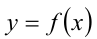 называется возрастающей на множестве
называется возрастающей на множестве 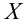 , если для любых двух значений
, если для любых двух значений 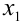 и
и 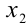 из этого множества таких, что
из этого множества таких, что 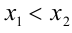 , выполняется неравенство
, выполняется неравенство 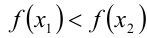 . Зафиксируем любые два значения
. Зафиксируем любые два значения 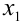 и
и 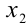 , из промежутка
, из промежутка 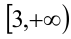 такие, что
такие, что 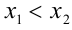 . Так как неравенство
. Так как неравенство 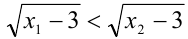 верно для таких
верно для таких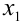 и
и 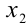 , то монотонное возрастание первой из функций доказано. Аналогично доказывается возрастание второй функции
, то монотонное возрастание первой из функций доказано. Аналогично доказывается возрастание второй функции 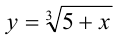 .
.
Итак, в левой части уравнения находится возрастающая функция (как сумма двух возрастающих функций). В правой части уравнения стоит постоянная функция 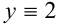 . Графики таких функций пересекаются не более чем в одной точке. Следовательно, уравнение имеет не более одного решения. Так как одно решение выше было найдено
. Графики таких функций пересекаются не более чем в одной точке. Следовательно, уравнение имеет не более одного решения. Так как одно решение выше было найдено 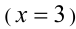 , то других решений нет.
, то других решений нет.
Пример №384.
Решить неравенство
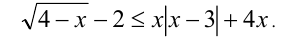
Решение:
Заметим, что функция 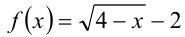 , расположен-ная в левой части неравенства, монотонно убывает при
, расположен-ная в левой части неравенства, монотонно убывает при 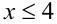 .
.
Действительно, возьмём произвольные числа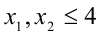 , <4 такие, что
, <4 такие, что 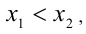 , и покажем, что
, и покажем, что 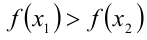 . В самом деле,
. В самом деле,
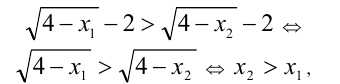
что верно. Так как для функции 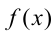 на луче
на луче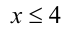 выполняется определение монотонно убывающей функции, то убывание
выполняется определение монотонно убывающей функции, то убывание 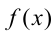 доказано.
доказано.
Заметим, далее, что функция в правой части неравенства
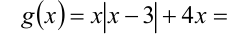
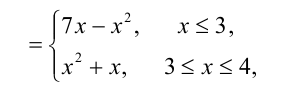
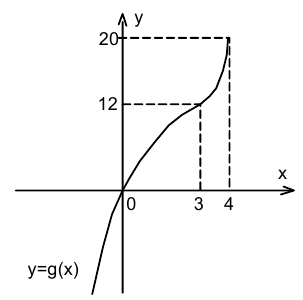
наоборот, возрастает при 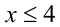 как функция, возрастающая на каждом из двух смежных промежутков
как функция, возрастающая на каждом из двух смежных промежутков 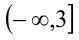 и
и 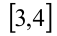 (см. рис.). Графики таких функций
(см. рис.). Графики таких функций 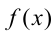 ) и
) и 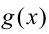 пересекаются не более чем в одной точке. Учитывая, что
пересекаются не более чем в одной точке. Учитывая, что 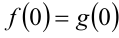 , получаем, что решением неравенства
, получаем, что решением неравенства 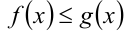 будет отрезок
будет отрезок 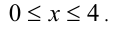
В частности, неравенства вида 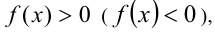 , где
, где 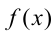 — возрастающая функция, а
— возрастающая функция, а 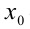 её единственный нуль, имеют своим решением промежуток
её единственный нуль, имеют своим решением промежуток 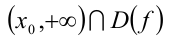 (соответственно промежуток
(соответственно промежуток 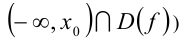 , где
, где 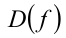 — область определения функции. Аналогично, если
— область определения функции. Аналогично, если 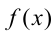 — убывающая функция, то решением неравенства
— убывающая функция, то решением неравенства 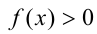 будет
будет 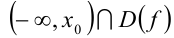 , а решением неравенства
, а решением неравенства 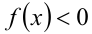 — промежуток
— промежуток 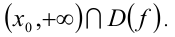
Пример №385.
Решить неравенство 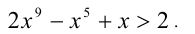
Решение:
Перепишем неравенство в виде 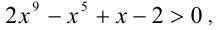 и обозначим
и обозначим 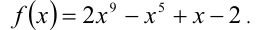 Требуется определить, при каких значениях переменной
Требуется определить, при каких значениях переменной 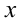 данная функция принимает положительные значения. Покажем, что функция возрастает на всей числовой прямой. Действительно, найдём её производную
данная функция принимает положительные значения. Покажем, что функция возрастает на всей числовой прямой. Действительно, найдём её производную 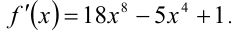 Так как дискриминант квадратного трёхчлена
Так как дискриминант квадратного трёхчлена 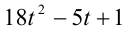 отрицателен, то
отрицателен, то 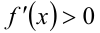 при всех
при всех 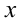 , т.е. функция монотонно возрастает. Но если функция непрерывна и монотонно возрастает на всей числовой прямой, то её график пересекает ось
, т.е. функция монотонно возрастает. Но если функция непрерывна и монотонно возрастает на всей числовой прямой, то её график пересекает ось 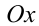 в единственной точке. Заметим, что
в единственной точке. Заметим, что 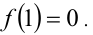 Осталось с учётом положительности значений функции выписать ответ. Ответ:
Осталось с учётом положительности значений функции выписать ответ. Ответ: 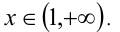
Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:
Эти страницы возможно вам будут полезны:

