Оглавление:
Метод неопределённых коэффициентов
Иногда для решения алгебраических задач с одной или несколькими переменными используют метод неопределённых коэффициентов. Суть метода состоит в том, что для исследуемого выражения подбирается подходящая параметрическая модель, которая описывает это выражение при всех значениях входящих в него переменных. Модель содержит в себе неизвестные параметры (неопределённые коэффициенты), подлежащие определению. Применение метода в конечном итоге сводится к составлению системы уравнений, из которой и находятся неопределённые коэффициенты и затем подставляются в математическую модель. К недостаткам метода можно отнести то, что получаемая система уравнений может оказаться громоздкой и поэтому трудной не только для нахождения решения, но даже для его подбора.
Пример №357.
Найти такие числа 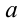 и
и 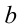 , что при всех
, что при всех 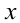 справедливо равенство
справедливо равенство
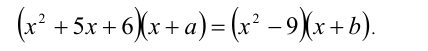
Решение:
Воспользуемся методом неопределённых коэффициентов. Раскроем скобки в левой и правой частях уравнения, и приведём образовавшиеся при этом многочлены 3-й степени к стандартному виду:
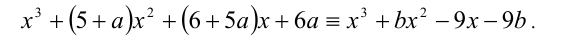
Учитывая, что два кубических многочлена тождественно (при всех 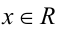 ) равны тогда и только тогда, когда равны коэффициенты при одинаковых степенях переменной
) равны тогда и только тогда, когда равны коэффициенты при одинаковых степенях переменной 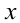 , выписываем систему:
, выписываем систему:
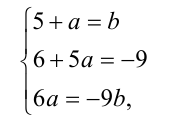
решая которую находим 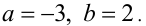
Пример №358.
Квадратный трёхчлен 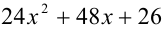 является разностью кубов двух линейных функций с положительными коэффициентами. Найти эти функции.
является разностью кубов двух линейных функций с положительными коэффициентами. Найти эти функции.
Решение:
Согласно условию, при всех действительных 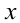 выполняется тождество
выполняется тождество
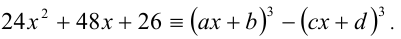
Раскроем кубы в правой части этого равенства и приведём образовавшийся кубический многочлен к стандартному виду:
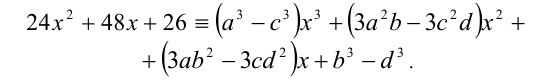
Используя условие тождественного равенства двух многочленов и приравнивая коэффициенты, получаем систему алгебраических уравнений
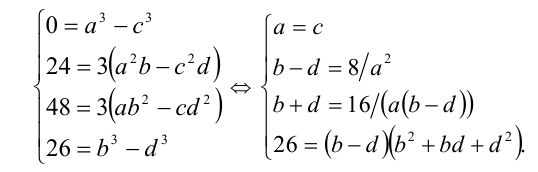
Из второго и третьего уравнений находим
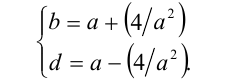
Подставляя в четвёртое уравнение, получим:
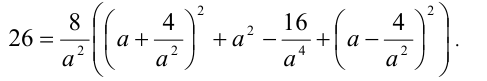
Умножим последнее равенство на 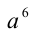 :
:
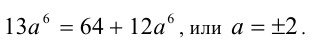
Учитывая, что по условию 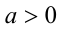 , имеем
, имеем 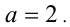 Тогда
Тогда 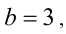
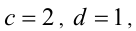 и искомые линейные функции имеют вид
и искомые линейные функции имеют вид 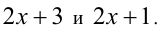
Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:
Эти страницы возможно вам будут полезны:

