Оглавление:
Метод «от частного к общему» пример решения
Пример №340.
Найти все значения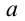 
и 
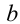такие, что для любого 
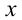из отрезка 
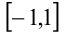будет выполняться неравенство 
.
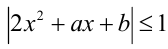Решение:
Раскроем модуль: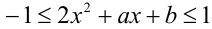 
, и решим задачу методом «от частного к общему».
Так как это неравенство, по условию, выполняется при всех 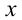из указанного отрезка, то, в частности, оно должно выполняться для 
:
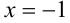Положив в неравенстве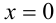 
и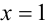 
, получим ещё два неравенства
и
Сложив неравенства (1) и (3), получим, что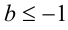 
. С учётом (2) это означает, что 
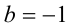. Подставляя это значение в (1) и (3), находим 
.
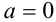Таким образом, если существуют числа 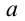и 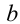, удовлетворяющие условию задачи, то это 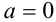, , 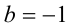и других решений задача иметь не может. Чтобы доказать, что найденные 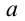и 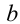являются решениями задачи, осталось проверить, что для любого 
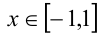справедливо неравенство 
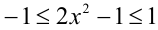, что верно. Ответ: , .
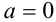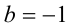Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:
Эти страницы возможно вам будут полезны:
