Оглавление:
Метод оценок
Метод оценок, суть которого в широком смысле слова состоит в том, что при анализе задачи используются полезные для её дальнейшего решения оценки неизвестных или выражений, получаемые на ОДЗ с привлечением производной или всевозможных неравенств. Например, одна из типичных ситуаций: решается уравнение
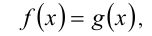
при этом, оценив независимо друг от друга возможные значения левой и правой частей уравнения, в ряде случаев (как раз тогда, когда этот метод дает положительный результат) обнаруживаем, что, например, левая часть уравнения при всех допустимых значениях неизвестных принимает значения меньшие либо равные некоторому числу, а правая, наоборот, — большие либо равные этому же числу значения. Иными словами, наибольшее значение левой части равно наименьшему значению правой части. Тогда делается вывод, что данное уравнение равносильно системе двух, вообще говоря, более простых уравнений, получаемых приравниванием отдельно левой и правой частей уравнения к данному числу. Существуют и другие разновидности метода оценок (см. п. 3.4 раздела 3).
Этот метод часто напрямую связан с группой функциональных методов, так как при оценивании выражений зачастую используются различные свойства функций, входящих в решаемое уравнение (например, ограниченность, монотонность). Возможные трудности связаны с необходимостью выполнить правильные оценки, привлекая для этих целей известные неравенства, производную и пр.
Пример №337.
Решить неравенство
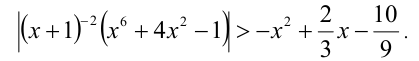
Решение:
Выделяя в правой части полный квадрат по 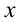 , получим
, получим 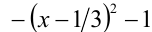 . Отсюда, учитывая неотрицательность модуля и ОДЗ, приходим к ответу. Ответ:
. Отсюда, учитывая неотрицательность модуля и ОДЗ, приходим к ответу. Ответ: 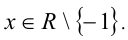
Пример №338.
Решить уравнение
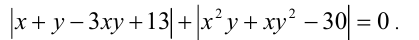
Решение:
Сумма двух неотрицательных выражений обращается в нуль тогда и только тогда, когда оба слагаемых одновременно равны нулю. Поэтому данное уравнение равносильно системе
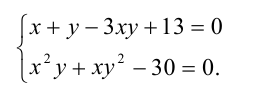
Данная система относится к группе симметрических систем, в которых каждое уравнение не меняет своего вида при одновременной замене 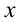 на
на 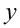 , а
, а 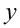 на
на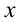 . Такие алгебраические системы решаются обычно при помощи двойной подстановки
. Такие алгебраические системы решаются обычно при помощи двойной подстановки 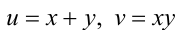 . Преобразовав уравнения системы к виду
. Преобразовав уравнения системы к виду
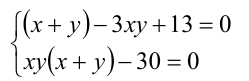
и сделав соответствующую замену, приходим к системе
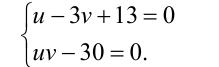
Далее решаем её методом подстановки:
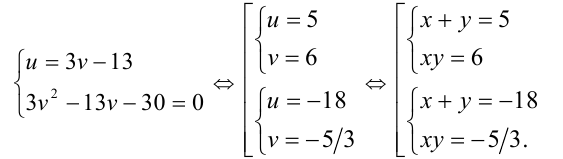
Первая из систем имеет два решения (2;3), (3;2), вторая — ещё два:
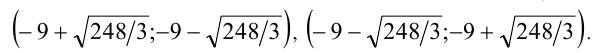
Объединяя эти решения, получаем ответ:
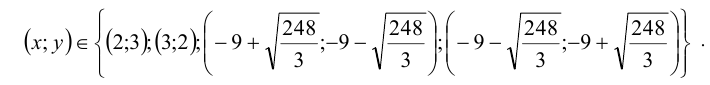
Пример №339.
Решить систему уравнений
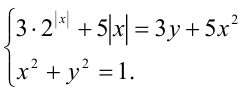
Решение:
Преобразуем систему к виду
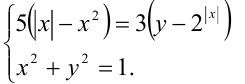
Из второго уравнения следуют оценки 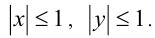 Так как
Так как 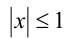 , то
, то 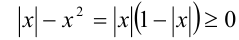 , т.е. левая часть первого из уравнений принимает неотрицательные значения. Так как
, т.е. левая часть первого из уравнений принимает неотрицательные значения. Так как 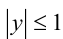 , то
, то 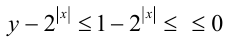 , т.е. правая часть того же уравнения неположительна. Это означает, что данное уравнение равносильно системе
, т.е. правая часть того же уравнения неположительна. Это означает, что данное уравнение равносильно системе
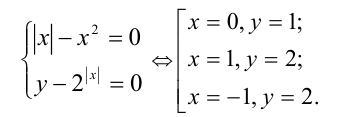
Только первая пара удовлетворяет второму уравнению исходной системы. Ответ :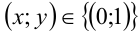 .
.
Другие примеры на метод оценок были приведены выше в пункте, посвященном использованию свойств модулей.
Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:
Эти страницы возможно вам будут полезны:

