Оглавление:
Разложение на множители
Иногда удаётся, перенося все слагаемые в уравнении (неравенстве) в одну сторону, разложить полученное выражение на множители. Разложение осуществляется различными способами, в том числе группировкой и вынесением общего множителя за скобку, рассмотрением данного уравнения как квадратного относительно какой-либо величины, с использованием формул сокращенного умножения и прочими приёмами. В результате уравнение на ОДЗ сводится к совокупности нескольких, вообще говоря, более простых уравнений, а неравенство может быть решено, например, методом интервалов или каким-либо иным способом.
Пример №323.
Решить неравенство
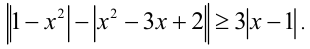
Решение задачи рассмотрено выше в пункте «Раскрытие модуля, используя его геометрический смысл».
Пример №324.
При каких значениях а уравнение имеет ровно три корня:
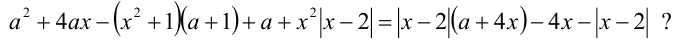
Решение:
Преобразуем данное уравнение, перенося все слагаемые в одну сторону, группируя их и выделяя общие множители:
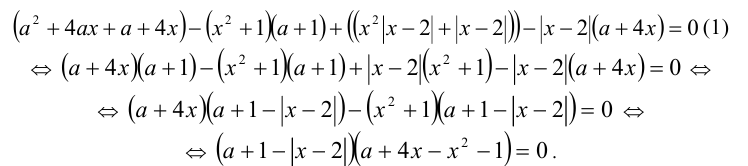
Таким образом, удалось разложить левую часть уравнения (1) на множители. Далее, уравнение распадается на совокупность двух уравнений
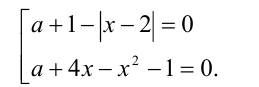
Приведём данную совокупность уравнений к виду
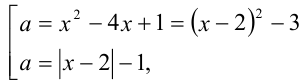
и далее будем решать оба уравнения, вводя систему координат, в которой на оси абсцисс откладываются значения неизвестной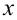 
, а на оси ординат — значения параметра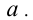 
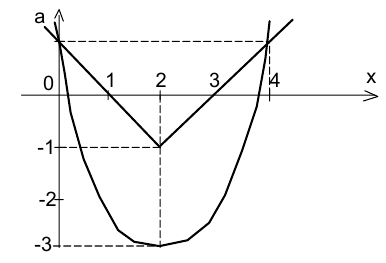
Графическим образом решений данной совокупности служит объединение графиков модуля и параболы. Из рисунка видно, что ровно три корня уравнение имеет только при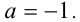 
Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:
Эти страницы возможно вам будут полезны:
