Оглавление:
Раскрытие модулей на ОДЗ
При решении задач с модулями не всегда сразу возникает необходимость в применении метода интервалов или каких-либо других способов избавления от модулей. Иногда бывает достаточно провести анализ ОДЗ, и в результате по крайней мере часть модулей удаётся однозначно раскрыть. Рассмотрим три примера.
Пример №274.
Решить уравнение 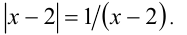
Решение:
Очевидно,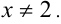 Более того, так как левая часть уравнения неотрицательна, то и равная ей правая часть должна быть неотрицательна, т.е.
Более того, так как левая часть уравнения неотрицательна, то и равная ей правая часть должна быть неотрицательна, т.е. 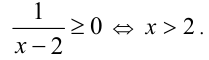
Но при 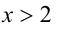 модуль раскрывается положительно, и, решая полученное уравнение
модуль раскрывается положительно, и, решая полученное уравнение 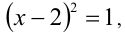 находим
находим 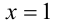 или
или 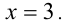 Только второе число удовлетворяет условию
Только второе число удовлетворяет условию 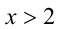 и поэтому будет решением.
и поэтому будет решением.
Пример №275.
Решить уравнение 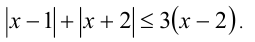
Решение:
Заметим, что левая часть уравнения положительна (как сумма двух неотрицательных слагаемых, одновременно не обращающихся в нуль). Следовательно, 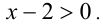 Но при
Но при 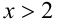 оба модуля раскрываются положительно, и, решая полученное неравенство, находим
оба модуля раскрываются положительно, и, решая полученное неравенство, находим 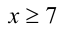 . Так как все такие
. Так как все такие 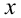 удовлетворяют условию
удовлетворяют условию 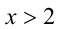 , то они являются решениями. Ответ:
, то они являются решениями. Ответ: 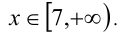
Пример №276.
Решить неравенство
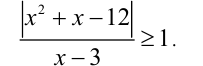
Решение:
Очевидно,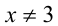 . Более того, так как дробь, по условию, больше 1, то она, как минимум, положительна. При этом числитель дроби положителен, а значит, и знаменатель должен быть положительным, т.е.
. Более того, так как дробь, по условию, больше 1, то она, как минимум, положительна. При этом числитель дроби положителен, а значит, и знаменатель должен быть положительным, т.е. 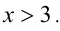 Перепишем неравенство в виде:
Перепишем неравенство в виде:
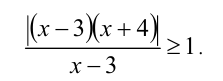
Видно, что при 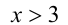 подмодульное выражение положительно, следовательно, модуль однозначно раскрывается, и получаем неравенство
подмодульное выражение положительно, следовательно, модуль однозначно раскрывается, и получаем неравенство 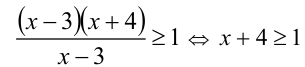 — верно при
— верно при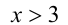 . Ответ:
. Ответ: 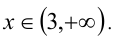
Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:
Эти страницы возможно вам будут полезны:

