Оглавление:
Метод областей — обобщение метода интервалов
Если требуется решить уравнение (неравенство) с двумя неизвестными x и у, например, вида
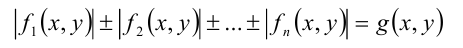
(под знаком модуля содержатся выражения от двух неизвестных), то прибегают к аналогу метода интервалов на плоскости — методу областей.
Отличие его от метода интервалов состоит в следующем. Если в методе интервалов приравнивались к нулю подмодульные выражения и находились точки x на числовой прямой, в которых каждое из подмодульных выражений могло поменять знак, то теперь, приравнивая выражения под знаком модуля к нулю, будем получать некоторые кривые, которые разбивают координатную плоскость на области. Перебирая поочерёдно все области, в каждой из них раскрывают с соответствующим знаком имеющиеся в задаче модули, и затем изображают графически в виде кривой или иной фигуры на плоскости решение полученного уравнения (неравенства) в рассматриваемой области. В заключение следует объединить полученные по всем областям результаты и пересечь их с ОДЗ.
Пример №269.
Изобразить на координатной плоскости геометрическое место точек (х;y), координаты которых удовлетворяют уравнению
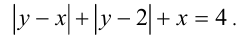
Решение:
Воспользуемся методом областей. Приравняв к нулю подмодульные выражения, получаем уравнения двух прямых y = x и у = 2. Указанные прямые разбивают всю координатную плоскость Оху на четыре области. Рассмотрим поочерёдно каждую из областей, раскрывая в ней модули.
Например, первый модуль раскрывается со знаком «плюс» там, где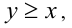 
т.е. во II и III областях, и со знаком «минус» соответственно в I и IV областях.
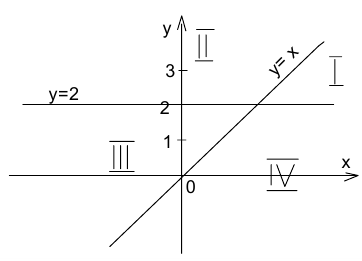
Второй модуль раскрывается со знаком «плюс» там, где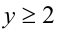 
т.е. в I и II областях, и со знаком «минус» соответственно в III и IV областях.
Область I: после раскрытия модулей уравнение принимает вид —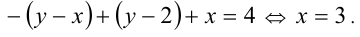 
Таким образом, в данной области искомое ГМТ представляет собой отрезок прямой 
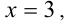попадающий в эту область.
Область II: после раскрытия модулей уравнение принимает вид
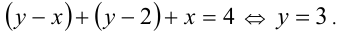
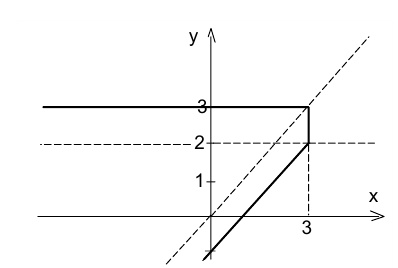
Таким образом, в данной области искомое ГМТ представляет собой часть прямой у = 3 , попадающую в эту область.
Область III: после раскрытия модулей уравнение принимает вид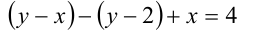
и не имеет решений. Поэтому в данной области ГМТ отсутствует.
Область IV: после раскрытия модулей уравнение принимает вид
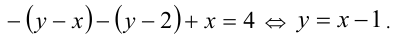
Таким образом, в данной области искомое ГМТ представляет собой часть прямой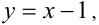 
попадающую в эту область. Объединяя полученные ГМТ, строим окончательно фигуру (см. рис. выше). Задача решена.
Пример №270.
Найти площадь фигуры, заданной неравенством
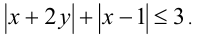
Решение:
Построим указанную фигуру. Прямые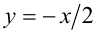 
и 
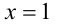разбивают координатную плоскость на четыре области.
В I области (см. рис.) оба модуля раскрываются положительно, и неравенство принимает вид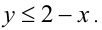 
Пересечение полуплоскос-ти, задаваемой этим неравенством, и I области, образует часть искомой фигуры. Во II области 1-й модуль раскрывается положительно, а второй — отрицательно, в результате получаем неравенство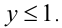
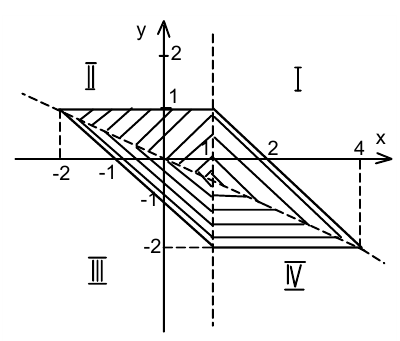
Достраиваем вторую часть фигуры. В III области, аналогично действуя, получаем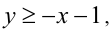 
а в IV области, соответственно, 
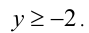Объединяя все четыре части, получаем искомую фигуру в виде параллелограмма.
Очевидно, что длина верхней стороны параллелограмма равна 3, длина высоты, проведённой к этой стороне (её роль выполняет меньшая диагональ параллелограмма), также равна 3. Искомая площадь фигуры равна произведению длин указанных отрезков. Ответ: 9 кв.ед.
Построение на плоскости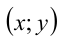 
фигуры, задаваемой уравнением
или неравенством
(знак 
заменяет любой из знаков неравенства), можно значительно упростить, если эта фигура обладает свойством симметрии относительно координатных осей или прямых, им параллельным. Так, если, например, функция 
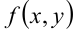чётна относительно переменной 
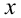, т.е. для всех допустимых 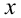и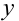 
выполняется равенство
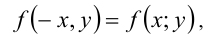
то фигура, определяемая уравнением (1) или неравенством (2), будет симметрична относительно прямой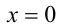 
ось ординат 
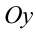), а если функция 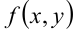чётна относительно переменной 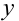, т.е. для всех допустимых 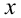и 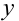выполняется равенство
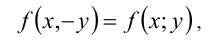
то фигура, определяемая (1) или (2), симметрична относительно прямой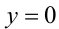 
(ось абсцисс 
).
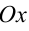Пользуясь аналогичными рассуждениями, можно заметить, что, например, уравнение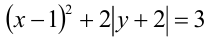 
задаёт на плоскости фигуру, симметричную относительно прямых 
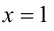и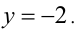 
В этом случае при построении данной фигуры достаточно изобразить её, например, только в области
, 
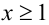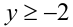, а затем достроить полученный участок симметрично осей симметрии фигуры.
Подумайте, какой вывод о свойствах фигуры можно сделать в случае, когда функция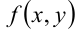 
удовлетворяет условию
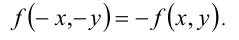
Пример №271.
Найти площадь фигуры, заданной неравенством
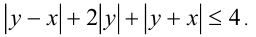
Решение:
Заметим, что при замене в данном неравенстве 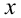на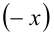 
значение функции в левой части неравенства не изменится.
Это означает, что данная фигура симметрична относительно оси ординат. Аналогично заметим, что ничего не изменится и при замене 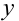на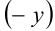
т.е. фигура к тому же обладает свойством симметрии относительно оси абсцисс.
Поэтому достаточно построить фигуру, например, в первой четверти, а затем отобразить её симметрично обеим координатным осям.
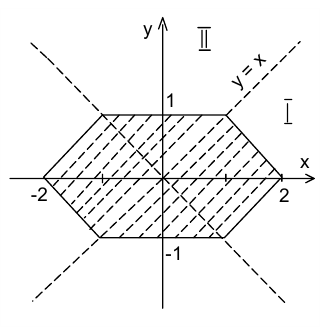
В области I (см. рис.) раскрываем модули и получаем,что
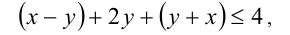
т.е.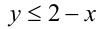 
. В области II соответственно получаем:
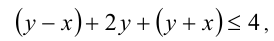
т.е.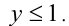 
Используя симметрию относительно координатных осей, достраиваем фигуру: это шестиугольник площади 6 кв.ед.
Пример №272.
Изобразить на координатной плоскости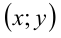 
множество точек, координаты которых удовлетворяют условию
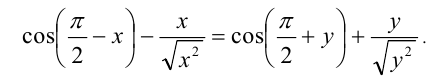
Решение:
Это условие равносильно условию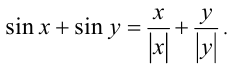 
ОДЗ: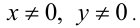
Так как функция 
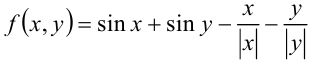удовлетворяет условию 
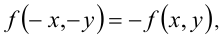то искомая фигура центрально симметрична относительно начала координат. Поэтому построим её вначале в 1-й и 4-й четвертях.
1) Пусть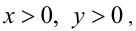 
тогда условие примет вид
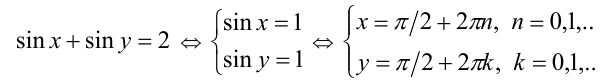
2) Пусть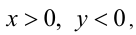 
тогда получим условие в виде
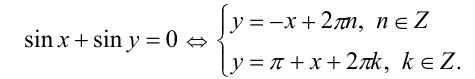
В 1-й и 4-й четвертях имеем бесконечную совокупность отдельных точек, образованных пересечениями соответствующих прямых (см. рис.):
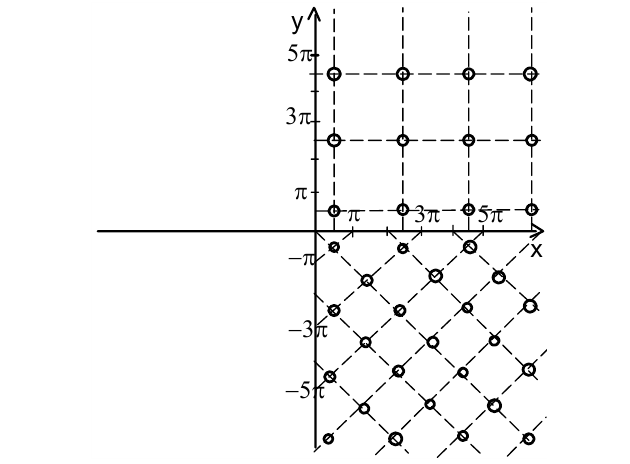
Для получения искомой фигуры осталось центрально симметрично достроить полученное множество в левую полуплоскость.
Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:
Эти страницы возможно вам будут полезны:
