Оглавление:
Метод интервалов
В отличие от рассмотренного выше приёма, основанного на раскрытии модулей по определению, метод интервалов оказывается эффективен в задачах, содержащих сразу несколько модулей.
Пусть, например, дано уравнение с одним неизвестным x вида
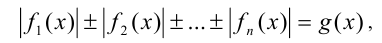
где 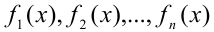 и
и 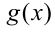 некоторые заданные функции.
некоторые заданные функции.
Чтобы решить его методом интервалов, надо сделать следующее.
1) Приравнять к нулю все подмодульные выражения 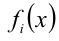 и решить полученные уравнения:
и решить полученные уравнения: 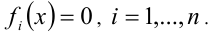 Допустим, решениями этой совокупности уравнений являются числа
Допустим, решениями этой совокупности уравнений являются числа 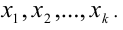 .
.
2) Найденные k чисел разбивают всю область допустимых значений переменной x на конечное число интервалов (отсюда название метода), на каждом из которых каждая из функций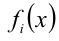 сохраняет определённый знак. Затем задача решается на каждом из этих интервалов.
сохраняет определённый знак. Затем задача решается на каждом из этих интервалов.
3) Возьмём, к примеру, первый из интервалов. Пусть это будет интервал 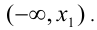 Подставляя поочерёдно любое удобное число x из этого интервала в подмодульные выражения и оценивая их знак, раскрываем каждый из модулей, по определению, либо со знаком «плюс», либо со знаком «минус». Технически это происходит так: если выражение под модулем положительно, то модуль опускается (заменяется обычными скобками); если же выражение под знаком модуля отрицательно, то модуль заменяется скобками, перед которыми ставится знак минус. Таким образом, в задаче не остается нераскрытых модулей, после чего она решается.
Подставляя поочерёдно любое удобное число x из этого интервала в подмодульные выражения и оценивая их знак, раскрываем каждый из модулей, по определению, либо со знаком «плюс», либо со знаком «минус». Технически это происходит так: если выражение под модулем положительно, то модуль опускается (заменяется обычными скобками); если же выражение под знаком модуля отрицательно, то модуль заменяется скобками, перед которыми ставится знак минус. Таким образом, в задаче не остается нераскрытых модулей, после чего она решается.
4) Из найденных решений отбираются те, которые принадлежат рассматриваемому интервалу 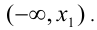 Только они будут решениями задачи. Затем переходим к следующему промежутку [
Только они будут решениями задачи. Затем переходим к следующему промежутку [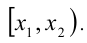
5) Рассмотрев по очереди все промежутки, объединяем в ответе решения, полученные на каждом из промежуточных интервалов.
Аналогичным образом можно решать и неравенства. Если в задаче имеется единственный модуль, то метод интервалов сводится фактически к раскрытию этого модуля по определению.
Теоретически метод интервалов может быть применён для решения большинства задач, содержащих модули. Однако, несмотря на его широкую распространённость, в экзаменационной практике встречаются задачи, для решения которых гораздо целесообразнее применять другие способы (задачи такого рода будут рассмотрены далее). Обратимся к примерам на использование метода интервалов.
Пример №264.
Решить уравнение
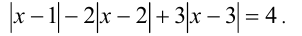
Решение:
Решим задачу методом интервалов. Определив три точки 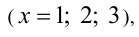 в которых подмодульные выражения обращаются в нуль (и меняют свои знаки), получаем четыре промежутка, и далее раскрываем модули последовательно на каждом из них.
в которых подмодульные выражения обращаются в нуль (и меняют свои знаки), получаем четыре промежутка, и далее раскрываем модули последовательно на каждом из них.
1) Пусть 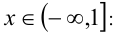 подставляя вместо x любое число, лежащее внутри этого промежутка, например (- 10), оцениваем знак каждого подмодульного выражения. Так как при x = — 10 имеем x — 1 < 0 , x — 2 < 0 , x — 3 < 0 , то все три модуля на данном промежутке раскроем со знаком «минус», и уравнение примет вид
подставляя вместо x любое число, лежащее внутри этого промежутка, например (- 10), оцениваем знак каждого подмодульного выражения. Так как при x = — 10 имеем x — 1 < 0 , x — 2 < 0 , x — 3 < 0 , то все три модуля на данном промежутке раскроем со знаком «минус», и уравнение примет вид
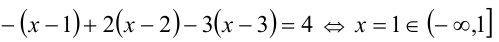 — решение.
— решение.
2) 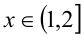 : подставляя вместо x , например, число 3/2 , оцениваем знаки выражений под модулями. При этом значении x имеем x -1 > 0 , x- 2 < 0 , x -3 < 0, поэтому первый модуль раскроем со знаком «плюс», а остальные два — со знаком «минус»:
: подставляя вместо x , например, число 3/2 , оцениваем знаки выражений под модулями. При этом значении x имеем x -1 > 0 , x- 2 < 0 , x -3 < 0, поэтому первый модуль раскроем со знаком «плюс», а остальные два — со знаком «минус»:
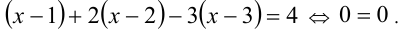
Полученное равенство не содержит x, а значит, выполняется при всех X из данного промежутка. Таким образом, весь промежуток войдёт в ответ.
3) 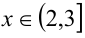 : действуя аналогично предыдущему, получим:
: действуя аналогично предыдущему, получим:
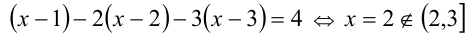
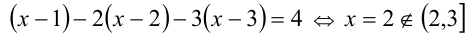 — нет решений.
— нет решений.
4) 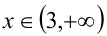 : на последнем промежутке уравнение примет вид
: на последнем промежутке уравнение примет вид
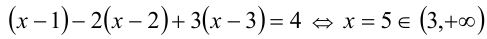
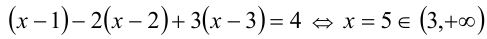 ) — решение.
) — решение.
Для получения ответа осталось объединить все найденные решения. Ответ: 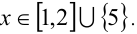
Полностью аналогичный подход используется и при решении неравенств с модулями.
Пример №265.
Решить неравенство 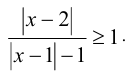
Решение:
Согласно методу интервалов, для освобождения от знаков абсолютной величины разобьём числовую ось на промежутки.
1) Если 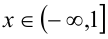 то
то 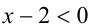 и
и 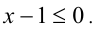 Значит, на этом промежутке оба модуля раскрываются со знаком «минус»:
Значит, на этом промежутке оба модуля раскрываются со знаком «минус»: 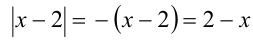 ,
,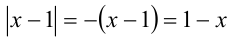 , и неравенство принимает вид
, и неравенство принимает вид 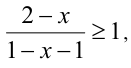 что равносильно неравенству
что равносильно неравенству 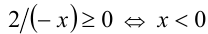 . Все эти значения x входят в рассматриваемый промежуток и поэтому являются решениями исходного неравенства.
. Все эти значения x входят в рассматриваемый промежуток и поэтому являются решениями исходного неравенства.
2) Если 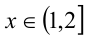 , то
, то 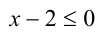 и
и 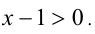 Значит, |
Значит, |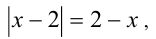
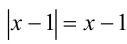 , и исходное неравенство принимает вид
, и исходное неравенство принимает вид 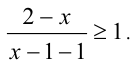 Оно не имеет решений, а следовательно, исходное неравенство не имеет решений в промежутке (1,2].
Оно не имеет решений, а следовательно, исходное неравенство не имеет решений в промежутке (1,2].
3) Наконец, если 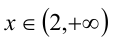 , то
, то 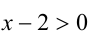 и
и 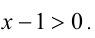 Значит,
Значит, 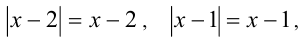 и исходное неравенство принимает вид
и исходное неравенство принимает вид 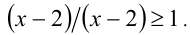 Множество решений этого неравенства состоит из двух промежутков
Множество решений этого неравенства состоит из двух промежутков 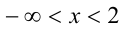 и
и 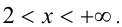 В рассматриваемую область попадает лишь второй из промежутков
В рассматриваемую область попадает лишь второй из промежутков 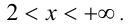 Все значения x из него и будут решениями исходного неравенства. Объединяя полученные решения, приходим к ответу. Ответ:
Все значения x из него и будут решениями исходного неравенства. Объединяя полученные решения, приходим к ответу. Ответ: 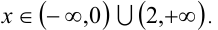
Метод интервалов используется и при решении задач, в которых имеются вложенные друг в друга модули.
Пример №266.
Решить уравнение
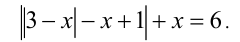
Решение:
Раскроем модули, начиная с внутреннего модуля. Для этого рассмотрим два случая.
1) 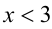 : имеем
: имеем 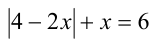 . Если при этом
. Если при этом 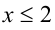 , то, раскрывая оставшийся модуль, получим
, то, раскрывая оставшийся модуль, получим 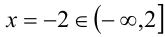 . Если же
. Если же 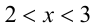 , то, раскрывая модуль, найдём
, то, раскрывая модуль, найдём 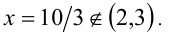
2) 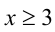 : имеем
: имеем 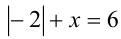 , т.е.
, т.е. 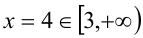 . Объединяя найденные решения, приходим к ответу:
. Объединяя найденные решения, приходим к ответу: 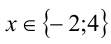 .
.
Особый интерес (и часто наибольшие трудности) представляют задачи, содержащие наряду с модулями параметры. Рассмотрим пример.
Пример №267.
Для каждого значения а найти все x, удовлетворяющие уравнению
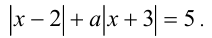
Решение:
Воспользуемся методом интервалов, для этого рассмотрим три промежутка, на которые точки x = 2 и x = — 3 разбивают ОДЗ уравнения (всю числовую прямую), и решим задачу на каждом из них.
1) Пусть 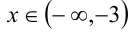 : раскрывая модули со знаком «минус», получаем линейное уравнение
: раскрывая модули со знаком «минус», получаем линейное уравнение 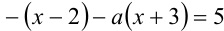 , и приводим его к виду
, и приводим его к виду

Если 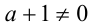 , то
, то 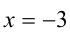 , однако это число не принадлежит рассматриваемому промежутку и поэтому не будет решением ни при каких а .
, однако это число не принадлежит рассматриваемому промежутку и поэтому не будет решением ни при каких а .
Если 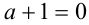 , то, подставляя
, то, подставляя 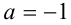 в уравнение (1), получаем уравнение
в уравнение (1), получаем уравнение 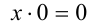 , которому удовлетворяет произвольное действительное x. С учётом рассматриваемого промежутка имеем
, которому удовлетворяет произвольное действительное x. С учётом рассматриваемого промежутка имеем 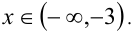
2) Пусть 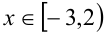 : раскрывая первый из модулей со знаком «минус», а второй со знаком «плюс», получаем уравнение
: раскрывая первый из модулей со знаком «минус», а второй со знаком «плюс», получаем уравнение 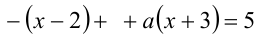 , и приводим его к виду
, и приводим его к виду

Если 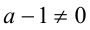 , то
, то 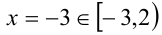 — решение.
— решение.
Если же 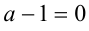 , то имеем уравнение
, то имеем уравнение 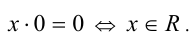 Учитывая промежуток, получаем
Учитывая промежуток, получаем 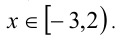
3) Пусть 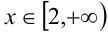 : раскрывая оба модуля со знаком «плюс», получаем уравнение
: раскрывая оба модуля со знаком «плюс», получаем уравнение 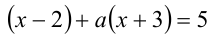 и приводим его к виду
и приводим его к виду

Если 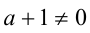 , то
, то 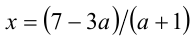 . Выясним, при каких значениях параметра а найденное число будет принадлежать рассматриваемому промежутку (т.е. являться решением). Для этого составим и решим неравенство
. Выясним, при каких значениях параметра а найденное число будет принадлежать рассматриваемому промежутку (т.е. являться решением). Для этого составим и решим неравенство
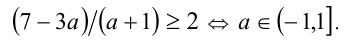
Если же 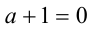 , то уравнение (3) приобретает вид
, то уравнение (3) приобретает вид 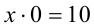 и, очевидно, не имеет решений. Наконец, объединяя полученные результаты, приходим к ответу.
и, очевидно, не имеет решений. Наконец, объединяя полученные результаты, приходим к ответу.
Ответ: при 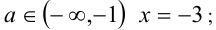 ; при
; при 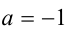
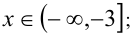
при , 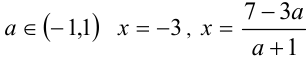 ; при
; при 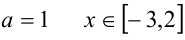 ;при
;при 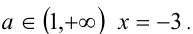
Метод интервалов используют и в случаях необходимости построения графика функции, если она содержит неизвестную под знаком модуля.
Пример №268.
Найти наименьшее значение функции
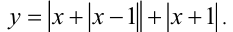
Решение:
Воспользуемся методом интервалов, начав раскрывать модули с модулей 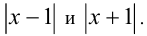
1) 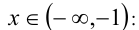 на этом интервале уравнение функции примет вид
на этом интервале уравнение функции примет вид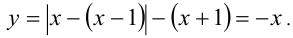
2) 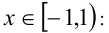 раскрывая модули, получаем
раскрывая модули, получаем 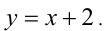
3) 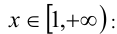 : раскрывая модули и упрощая функцию, получаем
: раскрывая модули и упрощая функцию, получаем
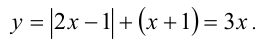
Итак, при помощи метода интервалов удалось найти аналитическое представление функции. Построим её график.
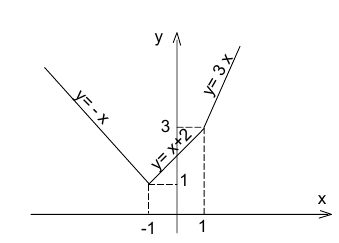
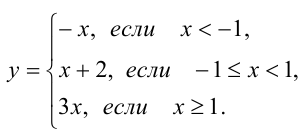
Из графика ясно, что функция принимает наименьшее значение, равное 1, при х = — 1.
Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:
Эти страницы возможно вам будут полезны:

