Оглавление:
Метод домножения на сопряжённое выражение
При использовании этого метода выражение, содержащее радикалы, одновременно умножается и делится на сопряжённое к нему выражение, в результате чего иррациональность пропадает, и решение задачи упрощается. Безусловно, при этом необходимо контролировать ситуацию, не допуская потери или приобретения лишних корней.
Приведём вначале определение того, какое иррациональное выражение называется сопряжённым к другому. Пусть S — некоторое выражение, содержащее радикалы (корни). Сопряжённым множителем относительно S называется всякое выражение К , не равное тождественно нулю, такое, что произведение S • К не содержит корней.
1) В частности, для выражения вида 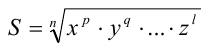 где
где 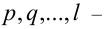 натуральные числа, меньшие n , сопряжённый множитель имеет вид
натуральные числа, меньшие n , сопряжённый множитель имеет вид
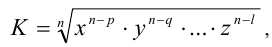 , так как
, так как 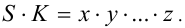
2) Для выражения вида 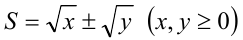 сопряжённый множитель есть
сопряжённый множитель есть 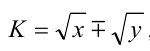 , так как
, так как 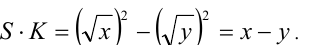
3) Для выражения вида 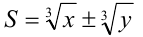 сопряжённый множитель есть
сопряжённый множитель есть 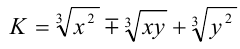 , так как
, так как 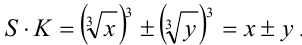
4) Для выражения вида 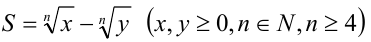 сопряжённый множитель есть
сопряжённый множитель есть
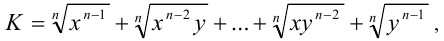
так как 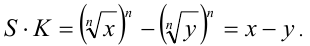
5) Для выражения вида 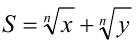 сопряжённый множитель находится на основании формул сокращённого умножения
сопряжённый множитель находится на основании формул сокращённого умножения
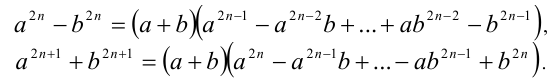
Рассмотрим примеры.
Пример №240.
Решить уравнение
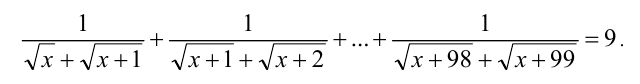
Решение:
Умножив и разделив каждую из дробей на выражение, сопряжённое к её знаменателю (все они положительны, поэтому в результате выполненных преобразований получим равносильное исходному уравнение):
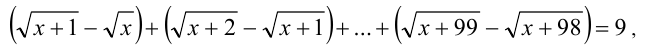
которое после упрощений примет вид 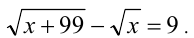
. Решая уравнение стандартным образом, получим ответ. Ответ: 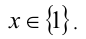
Пример №241.
Решить неравенство
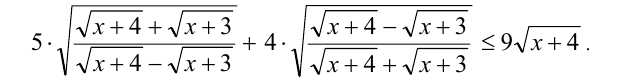
Решение:
Преобразуем подкоренное выражение у первого слагаемого в левой части неравенства, домножив числитель и знаменатель дроби на положительное выражение 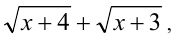 сопряжён-ное к знаменателю:
сопряжён-ное к знаменателю:
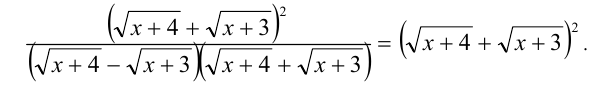
Аналогично преобразуем второе слагаемое
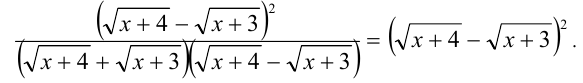
Учитывая, что под внешними корнями в левой части неравенства находятся полные квадраты, извлекаем квадратные корни, и решаемое неравенство принимает вид
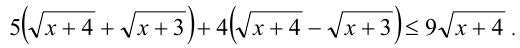
После упрощения получаем 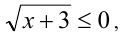 что даёт единственное решение
что даёт единственное решение 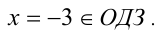 Ответ:
Ответ: 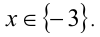
Пример №242.
Найти наименьшее значение функции 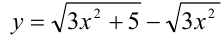 на отрезке [0,3].
на отрезке [0,3].
Решение:
Рассмотрим способ решения, не использующий производную этой функции. Преобразуем выражение, определяющее функцию, умножив и разделив его на выражение 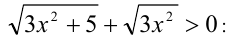
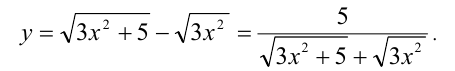
Теперь хорошо видно, что на отрезке [0,3] данная (непрерывная) функция определена и монотонно убывает, а значит, достигает своего наименьшего значения на правом конце отрезка, т.е. при x = 3 :
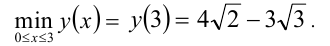
Пример №243.
Решить уравнение
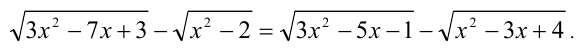
Решение:
Перепишем уравнение в виде:
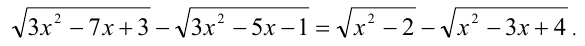
Применяя метод домножения на сопряжённое выражение, преобразуем левую и правую части уравнения:
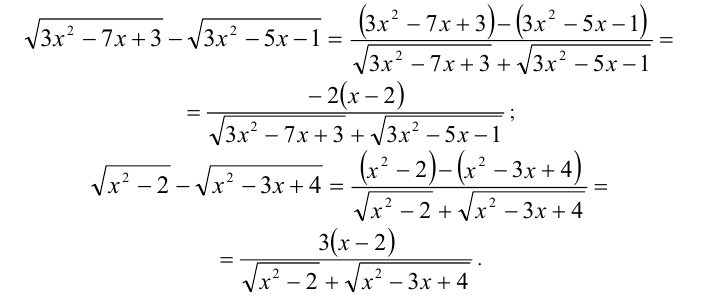
Тогда уравнение примет вид
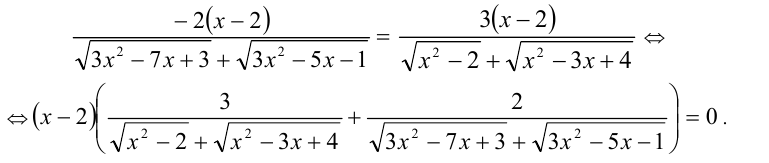
Это уравнение имеет единственное решение x = 2 , которое, как показывает проверка, удовлетворяет исходному уравнению. Других решений нет, поскольку выражение во вторых скобках строго положительно. Ответ: 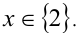
Пример №244.
Решить неравенство
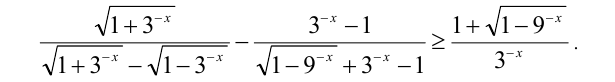
Решение:
Неравенство заменой 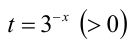 сводится к алгебраическому:
сводится к алгебраическому:
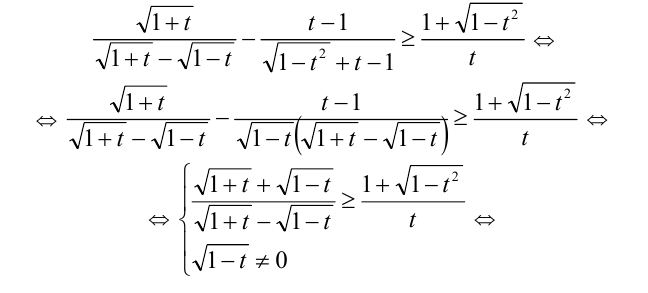
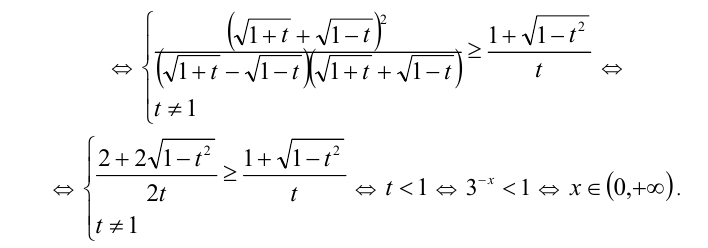
Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:
Эти страницы возможно вам будут полезны:

