Оглавление:
Метод интервалов для решения неравенств
Наряду с указанным выше общим методом, неравенства (рациональные алгебраические в том числе) часто решаются методом интервалов (не путать с методом интервалов для задач с модулями). Метод интервалов, пожалуй, является одним из самых распространённых методов решения неравенств вида
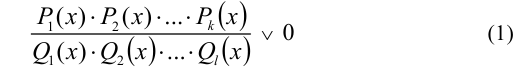
(количество сомножителей 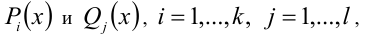 в числителе и знаменателе дроби, а также знак неравенства могут быть произвольными). Слово «обобщённый» перед словосочетанием «метод интервалов» используют обычно в тех случаях, когда множители в левой части неравенства не имеют чисто алгебраический вид. Суть метода состоит в следующем.
в числителе и знаменателе дроби, а также знак неравенства могут быть произвольными). Слово «обобщённый» перед словосочетанием «метод интервалов» используют обычно в тех случаях, когда множители в левой части неравенства не имеют чисто алгебраический вид. Суть метода состоит в следующем.
1) Все члены неравенства переносятся в одну сторону (например, в левую часть) и приводятся к общему знаменателю (т.е. неравенство приводится к виду (1)).
2) Определяются критические точки, т.е. точки, в которых числитель или знаменатель обращаются в нуль. Для этого решаются уравнения 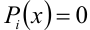 и
и 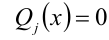 . При этом точки, обращающие в нуль знаменатель, следует «выколоть», а остальные — в зависимости от строгости или нестрогости решаемого неравенства.
. При этом точки, обращающие в нуль знаменатель, следует «выколоть», а остальные — в зависимости от строгости или нестрогости решаемого неравенства.
3) Критические точки наносятся на числовую прямую, разбивая сё (в общем случае — ОДЗ) на интервалы, в каждом из которых функция, находящаяся в левой части неравенства, сохраняет знак.
4) Определяется знак на крайнем справа интервале, что обозначается на числовой прямой с помощью знака «+» или «-».
5) Определяются знаки на остальных интервалах. В частности, при переходе через очередную критическую точку знак меняется на противоположный, если критическая точка является корнем нечётной кратности (т.е. встречается нечётное число раз среди корней числителя и знаменателя), и знак сохраняется, если точка имеет чётную кратность (или соответствующий множитель находится, например, под знаком модуля). Если числитель и знаменатель имеют совпадающие критические точки, то предварительно необходимо произвести сокращение, «выколов» данные точки на числовой оси.
6) Множеством решений неравенства является объединение интервалов с соответствующим знаком, при этом в случае нестрогого неравенства к этому множеству добавляются корни числителя.
Подчеркнём, что этим методом решаются не только алгебраические неравенства.
Пример №212.
Решить неравенство
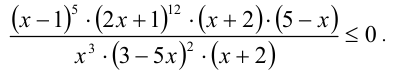
Решение:
Запомнив, что 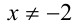 , вначале сократим числитель и знаменатель на общий множитель (х + 2):
, вначале сократим числитель и знаменатель на общий множитель (х + 2):
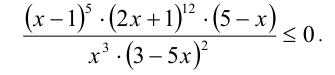
Найдём остальные критические точки, это x = 1, х = -1/2, x = 5, x = 0, x=3/5, и нанесём все точки (включая x = -2) на числовую прямую ,выколов те из них, которые обращают в нуль знаменатель дроби (x = — 2, x = 0, x = 3/5):

Оценим знак левой части неравенства на крайнем справа промежутке x > 5 . Для этого подставим любое число из этого промежутка, например 10, в выражение слева от знака равенства. Получим знак «-». Начнём рисовать кривую знакоопределённости для левой части неравенства. На рассмотренном промежутке изобразим её ниже числовой прямой, что символизирует отрицательный знак. Теперь начинаем мысленно «движение» справа налево вдоль оси x. Доходим до точки x = 5 . Чтобы выяснить, поменяется ли в этой точке знак левой части неравенства, найдём множитель (5 — х) в числителе, который обращается в нуль при этом значении. Он имеет нечётную степень, равную 1, и, следовательно, при прохождении справа налево через эту точку этот множитель (а с ним и вся левая часть) поменяет знак. На промежутке 1 < x < 5 общий знак будет «плюс», а кривая знакоопределённости пойдёт выше оси x .
Продолжаем «движение» налево, подходим к точке x = 1. Выясним, поменяет ли знак левая часть неравенства при прохождении через эту точку. Найдём множитель, из которого мы определили данную критическую точку, это 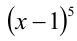 . Так как степень, равная 5, нечётная, то этот множитель, а с ним и вся левая часть поменяют знак, и кривая знакоопределённости пойдёт вниз. И так далее… Очевидно, в точке x = 0 знак левой части поменяется на противоположный, а в точках x = -2 , х = -1/2 , x = 3/5 — сохранится.
. Так как степень, равная 5, нечётная, то этот множитель, а с ним и вся левая часть поменяют знак, и кривая знакоопределённости пойдёт вниз. И так далее… Очевидно, в точке x = 0 знак левой части поменяется на противоположный, а в точках x = -2 , х = -1/2 , x = 3/5 — сохранится.
Когда кривая полностью построена, нужно лишь, учитывая знак неравенства 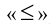 , отобрать те промежутки, которые лежат ниже числовой прямой, не забывая про те значения x, которые обращают числитель в нуль (в данном случае это х = -1/2 ). Таким образом, получаем окончательный ответ.
, отобрать те промежутки, которые лежат ниже числовой прямой, не забывая про те значения x, которые обращают числитель в нуль (в данном случае это х = -1/2 ). Таким образом, получаем окончательный ответ.
Ответ: 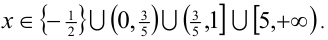
Рассмотрим применение метода интервалов к решению задачи.
Пример №213.
Решить неравенство
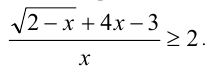
Решение:
ОДЗ: 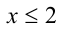 . Перепишем неравенство:
. Перепишем неравенство: 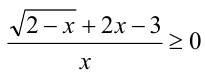 и воспользуемся методом интервалов. Найдём все значения неизвестной x, при которых числитель и знаменатель дроби обращаются в нуль. Для этого решим уравнение
и воспользуемся методом интервалов. Найдём все значения неизвестной x, при которых числитель и знаменатель дроби обращаются в нуль. Для этого решим уравнение
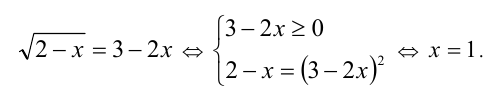
Итак, на ОДЗ имеем две критические точки x = 0 и x = 1, в которых числитель или знаменатель дроби обращаются в нуль (точку x = 0 при этом следует «выколоть»). Определим знак левой части неравенства на интервалах, на которые эти точки разбивают ОДЗ.
При x < 0 числитель и знаменатель отрицательны, а значит, их отношение положительно. При 0 < x < 1 числитель ещё отрицателен, а знаменатель положителен, поэтому их отношение отрицательно. При 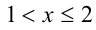 числитель и знаменатель, как и их отношение, положительны. Построим кривую знакоопределённости для левой части неравенства:
числитель и знаменатель, как и их отношение, положительны. Построим кривую знакоопределённости для левой части неравенства:

С учётом знака неравенства выписываем ответ: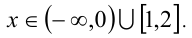
Замечание. Можно было на этапе определения знака дроби поступить иначе: найти знак этой дроби, например на промежутке ч < 0 (подставив любое удобное значение x, скажем, x = -2 ), а затем, двигаясь вдоль оси xслева направо, лишь отслеживать, меняется ли знак дроби в каждой из критических точек (он, очевидно, будет меняться в каждой из них).
Пример №214.
При всех значениях параметра а решить неравенство
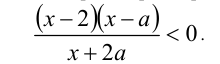
Решение:
Найдём критические точки: 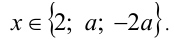 . Приравнивая их друг к другу попарно, найдём все значения параметра, при которых эти точки совпадают:
. Приравнивая их друг к другу попарно, найдём все значения параметра, при которых эти точки совпадают: 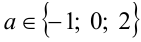 . Рассмотрим четыре случая.
. Рассмотрим четыре случая.
1) 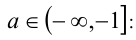 подставляя в выражения для критических точек в качестве а любую внутреннюю точку промежутка
подставляя в выражения для критических точек в качестве а любую внутреннюю точку промежутка 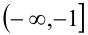 (например,
(например, 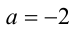 ), определяем порядок, в котором критические точки располагаются на числовой прямой x. При рассматриваемых а они оказываются упорядоченными так: а, 2, -2а . После этого методом интервалов решаем неравенство:
), определяем порядок, в котором критические точки располагаются на числовой прямой x. При рассматриваемых а они оказываются упорядоченными так: а, 2, -2а . После этого методом интервалов решаем неравенство:

Итак, при указанных значениях а получили решения: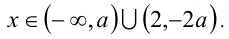
Замечание. При а = — 1 интервал (2,-2а) вырождается (пропадает), и ответ будет иметь вид 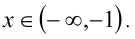
2) 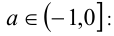 опять подставляем любую внутреннюю точку а из данного промежутка (например, а= -1/2 ) в выражения для критических точек и определяем порядок, в котором эти точки располагаются на числовой прямой. Затем методом интервалов решаем неравенство:
опять подставляем любую внутреннюю точку а из данного промежутка (например, а= -1/2 ) в выражения для критических точек и определяем порядок, в котором эти точки располагаются на числовой прямой. Затем методом интервалов решаем неравенство:

Итак, при 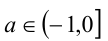 получили решения:
получили решения: 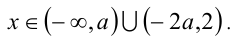
3) 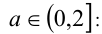 поступая аналогичным образом, находим:
поступая аналогичным образом, находим:

Итак, при 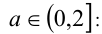 получили решения:
получили решения: 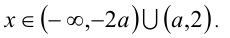
Замечание. При а= 2 интервал (a,2) вырождается (пропадает), и ответ будет иметь вид 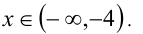
4) Наконец, в случае 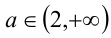 имеем
имеем

Поэтому при 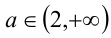 решениями будут
решениями будут 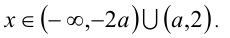 .
.
В ответе объединяем все полученные результаты.
Ответ:
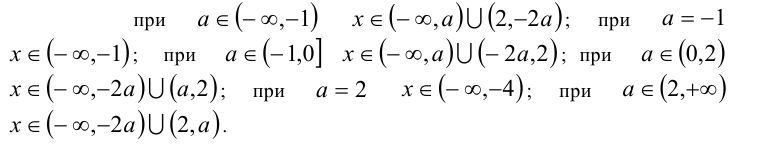
Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:
Эти страницы возможно вам будут полезны:

