Оглавление:
Графический подход (метод координат)
Графический подход обладает большой наглядностью, что, безусловно, можно отнести к его достоинствам, но имеет тот недостаток, что не всегда с его помощью можно определить точные значения решений. Чаще он используется для обоснования наличия решений в задаче, а также при оценке их количества.
Пример №201.
Построить на плоскости Оаb геометрическое место точек (a;b), для которых у уравнения
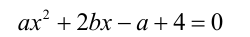
а) нет решений; б) ровно одно решение; в) ровно два решения.
Решение:
Найдём дискриминант: 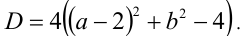
а) Уравнение не имеет решений тогда и только тогда, когда
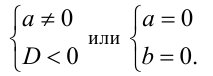
Искомое ГМГ представляет собой объединение открытого круга радиуса 2 с центром в точке (2;0) и точки начала координат.
б) Уравнение имеет ровно 1 решение тогда и только тогда, когда
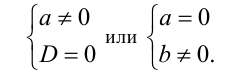
Искомое ГМГ представляет собой объединение окружности радиуса 2 с центром в точке (2;0) и оси ординат (с выколотой точкой начала координат).
в) Уравнение имеет ровно 2 решения тогда и только тогда, когда
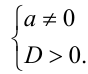
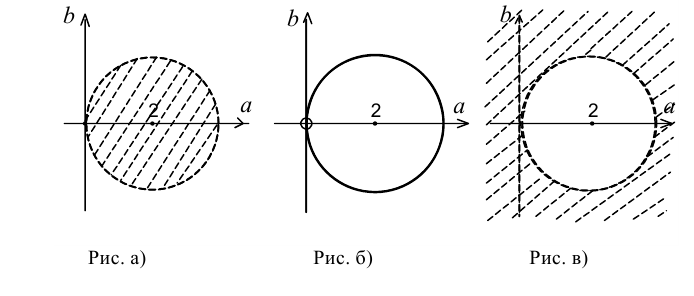
Искомое ГМГ представляет собой внешнюю часть круга радиуса 2 с центром в точке (2;0) (без оси ординат).
Соответствующие фигуры изображены выше на рисунках.
Пример №202.
Прямая 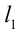 , проходит через точки (-3;2) и (l;l) координатной плоскости. Прямая
, проходит через точки (-3;2) и (l;l) координатной плоскости. Прямая 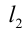 , проходит через точку ( — 5;4) и перпендикулярна прямой
, проходит через точку ( — 5;4) и перпендикулярна прямой 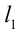 . Найти координаты точки пересечения прямых
. Найти координаты точки пересечения прямых 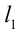 и
и 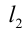 .
.
Решение:
Пусть у = ax +b — уравнение прямой 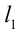 . Найдём коэффициенты а и b :
. Найдём коэффициенты а и b :
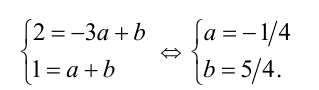
Если у = cx + d — уравнение прямой 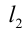 , то по условию
, то по условию
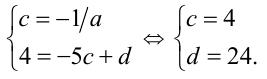
Для точки (x ; y) пересечения прямых 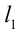 и
и 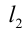 имеем
имеем
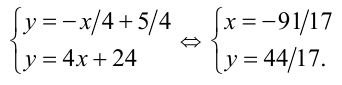
Пример №203.
Сколько различных корней имеет уравнение
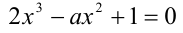
при различных значениях параметра а ?
Решение:
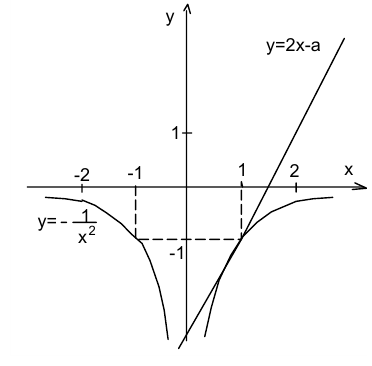
Перепишем, например, уравнение в эквивалентном виде
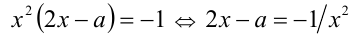
и решим его графически. Для этого построим в одной прямоугольной системе координат графики дробно-рациональной 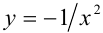 и линейной
и линейной 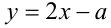 функций. Определим, при каком значении параметра а прямая
функций. Определим, при каком значении параметра а прямая 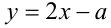 касается кривой
касается кривой 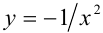 . Выпишем для этого уравнение касательной к графику этой функции в точке
. Выпишем для этого уравнение касательной к графику этой функции в точке 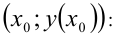
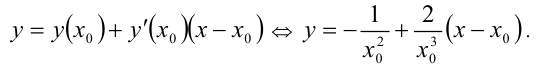
Данная касательная и прямая 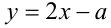 параллельны тогда и только тогда, когда их угловые коэффициенты равны:
параллельны тогда и только тогда, когда их угловые коэффициенты равны: 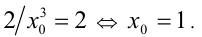
Подставим 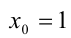 в уравнение касательной:
в уравнение касательной: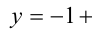
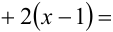
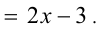
Отсюда получаем, что касание происходит при а = 3.
Ответ: при а < 3 — 1 решение; при а = 3 -2 решения; при а > 3 -3 решения.
Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:
Эти страницы возможно вам будут полезны:

