Оглавление:
Однородные уравнения
Алгебраический многочлен f(x,y) с двумя переменными x и у называется однородным многочленом n -й степени относительно этих переменных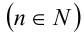 
, если при любом 
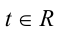имеет место тождество
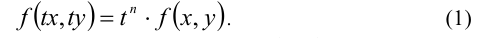
Это означает, что однородный многочлен n-й степени f (х, у) можно представить в виде
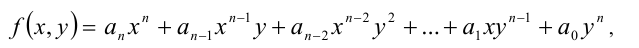
где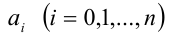 
— коэффициенты многочлена, одновременно не обращающиеся в нуль.
Уравнение f(x,y) = 0 называется однородным алгебраическим уравнением n -й степени с двумя неизвестными x,у, если f(x,y) — однородный многочлен n-й степени относительно этих переменных.
Например, уравнение вида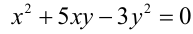 
является однородным уравнением 2-й степени относительно неизвестных x и у . Действительно, достаточно проверить выполнение условия (1). При одновременной замене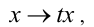 
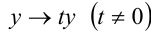, получим
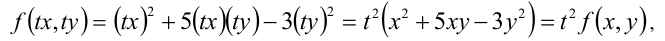
т.е. условие (1) из определения выполняется (n = 2).
Аналогично, уравнение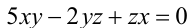 
есть однородное уравнение 2-й степени по отношению к неизвестным x,y,z , поскольку при замене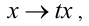 
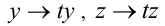получаем
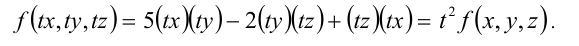
Итак, однородное алгебраическое уравнение — это уравнение, не меняющее своего вида при одновременном умножении всех его неизвестных на одно и то же число, отличное от нуля. Можно распространить понятие однородности на случай неалгебраических уравнений.
Пусть р(х) и q(x) — две произвольные функции, определённые на одном и том же множестве,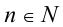 
.
Однородным уравнением n -й степени относительно функций р(х), q(x) называется уравнение вида
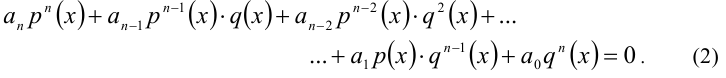
В частности, если функции р(х) и q(x) являются целыми алгебраическими многочленами, то и уравнение (2) будет относиться к аналогичному классу. В качестве другого примера рассмотрим уравнение вида
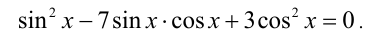
Оно является однородным тригонометрическим уравнением 2-й степени относительно функций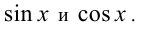 
Перейдём к процедуре решения уравнения (2).
Если хотя бы один из коэффициентов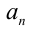 
или 
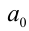обращается в нуль, то левая часть уравнения легко раскладывается на множители. В результате уравнение оказывается равносильно на ОДЗ совокупности двух уравнений. Например, если 
, 
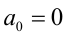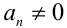то получим совокупность
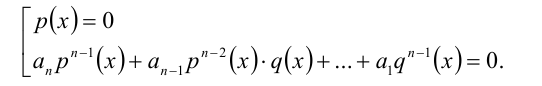
Если же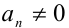 
и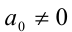 
, то для решения однородного уравнения (2) необходимо рассмотреть два возможных случая.
1) Если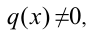 
то, поделив обе части уравнения на 
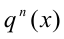и обозначив после этого отношение p(x)/q(x) через t , получим алгебраическое уравнение n -й степени относительно t:
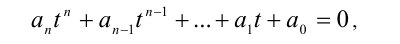
решив которое и сделав обратную подстановку, найдём часть решений однородного уравнения.
2) Если q(х) = 0. то, подставив в уравнение вместо q(x) нуль, получим, что тогда и р(х) должно обращаться в нуль. Таким образом, этот случай сводится к решению системы уравнений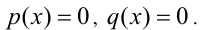 
Осталось объединить все найденные решения. Уравнение (2) решено. Обратимся к примерам.
Пример №185.
Решить уравнение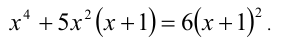 
Решение:
Перепишем уравнение: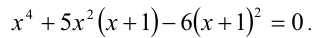 
Видно, что это однородное уравнение 2-й степени относительно функци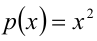й 
и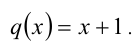
1) Пусть х + 1 = 0 , но система 
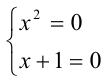решений не имеет.
2) Пусть теперь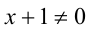 
. Поделив на 
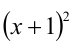и обозначив 
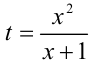, придём к квадратному уравнению 
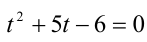. Оно имеет два корня 
, 
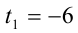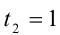. Возвращаясь к переменной x , приходим к совокупности двух уравнений
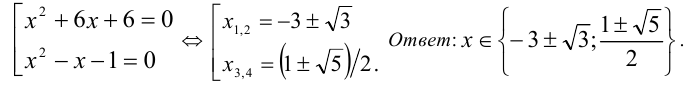
Пример №186.
Решить в целых числах уравнение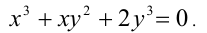 
Решение:
Заметим, что если у = 0, то x = 0, и, значит, пара (0;0) удовлетворяет уравнению. Пусть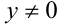 
, тогда поделим обе части уравнения на 
:
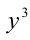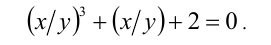
Обозначим t = x/у, тогда имеем кубическое уравнение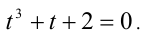 
Подбором находим корень t = — 1. Делением многочлена 
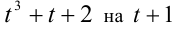получаем: 
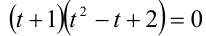Убеждаемся в том, что данное кубическое уравнение имеет единственный корень t = — 1, что соответствует у = — x . Положим x = р, где р — произвольное целое число, не равное 0. Тогда у = — р , и имеем бесконечно много решений в виде пар чисел (р;- р), 
, 
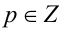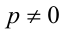. Объединяя все полученные решения, приходим к ответу.
Ответ: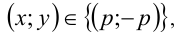
где .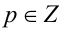
Пример №187.
Для каждого действительного значения параметра а решить уравнение
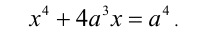
Решение:
Заметим, что данное уравнение можно рассмотреть как однородное алгебраическое уравнение 4-й степени относительно x и а.
1) Если а = 0 , то х = 0 .
2) Если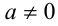 
, то поделим на 
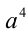, и положим 
:
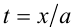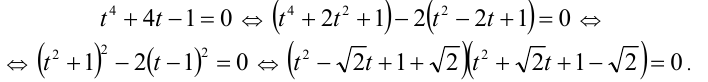
Первый сомножитель в нуль не обращается, а второй имеет два корня
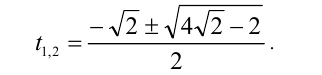
Ответ: при а = 0 единственное решение x = 0 ;
при 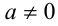два решения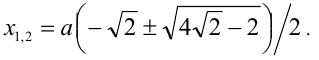 
Пример №188.
Найти действительные корни уравнения
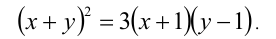
Решение:
Данное уравнение в исходном виде не является однородным, но может быть сведено преобразованиями к однородному. Действительно, достаточно привести его к виду
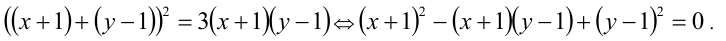
Получили однородное уравнение 2-й степени относительно x + 1 и у — 1.
1) Если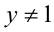 
, то, поделив на 
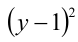и обозначив 
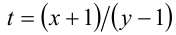, получим 
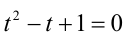нет решений.
2) Если у = 1, то, подставляя в уравнение, находим x = — 1 .
Ответ: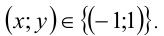 
Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:
Эти страницы возможно вам будут полезны:
