Оглавление:
Двучленные, трёхчленные и биквадратные уравнения
Двучленным называется уравнение вида
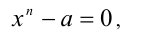
т.е.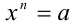 
, где
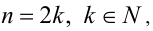Если 
и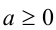 
, то уравнение имеет два различных действительных решения 
Если 
, 
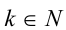, то при всех а уравнение имеет корнем только действительное число 
(кратности п ). Например, уравнение 
имеет два различных корня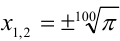 
, а уравнение 
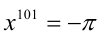имеет один корень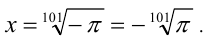 
Уравнение вида 
называется трёхчленным уравнением. При n = 2 трёхчленное уравнение принято называть биквадратным:
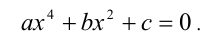
С помощью подстановки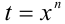 
трёхчленное уравнение сводится к квадратному уравнению 
В зависимости от n и коэффициентов а,b, c трёхчленное уравнение может не иметь решений, иметь одно, два, три и четыре различных действительных корня.
Пример №184.
Уравнение 
где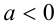 
. имеет одним из корней число x = 3 . Найти действительные корни уравнения
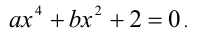
Решение:
Согласно теореме Виета для квадратного уравнения,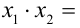 
. Отсюда заключаем, что его корни имеют разные знаки, и так как 
,то неизвестный второй корень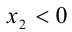 
. Решим теперь биквадратное уравнение. Сделаем замену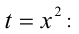
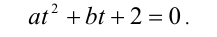
Заметим, что коэффициенты этого уравнения совпадают с коэффициентами исходного квадратного уравнения, а значит, эти уравнения имеют одинаковые корни. По доказанному выше, один из корней последнего уравнения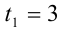 
другой
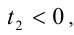следовательно, решение биквадратного уравнения сводится к решению совокупности двух уравнений
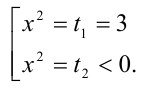
Первое уравнение имеет два действительных корня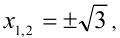 
. , а второе корней не имеет.
Ответ:
Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:
Эти страницы возможно вам будут полезны:
