Оглавление:
Теоремы о свойствах алгебраических многочленов
Пусть 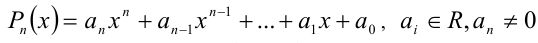 , — алгебраический многочлен n -й степени
, — алгебраический многочлен n -й степени 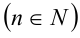 .
.
Теорема 1 (о разложении многочлена произвольной степени на произведение линейных и квадратичных множителей). Многочлен 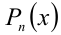 может быть представлен единственным образом в виде произведения многочленов, степень каждого из которых не выше второй.
может быть представлен единственным образом в виде произведения многочленов, степень каждого из которых не выше второй.
Теорема 2. Многочлен нечётной степени имеет хотя бы один действительный корень.
Теорема 3 (основная теорема алгебры). Многочлен n -й степени имеет ровно n корней (действительных и комплексных), в том числе действительных не больше n (сучётом их кратности).
Теорема 4. Если на концах некоторого отрезка [a, b ] значения многочлена имеют разные знаки, то на интервале (а, b) существует хотя бы один корень этого многочлена.
Заметим, что аналогичное утверждение справедливо не только для многочленов, но и для любой непрерывной на отрезке [ a,b ] функции.
Теорема 5 (условие тождественного равенства двух многочленов). Два алгебраических многочлена
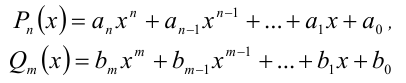
тождественно равны (т.е. равны при всех 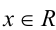 ) тогда и только тогда, когда равны степени многочленов n = m и совпадают коэффициенты при равных степенях x , т.е.
) тогда и только тогда, когда равны степени многочленов n = m и совпадают коэффициенты при равных степенях x , т.е. 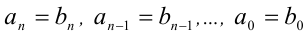 .
.
Пример №169.
Определить три числа p, q и r такие, что равенство 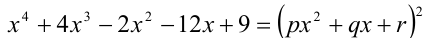 выполняется для любого значения переменной x.
выполняется для любого значения переменной x.
Решение:
Раскроем (вспомним соответствующую формулу сокращённого умножения) квадрат в правой части и приведём полученный многочлен к стандартному виду:
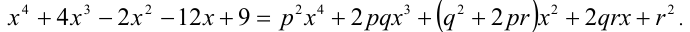
Многочлены, стоящие слева и справа от знака равенства, тождественно равны тогда и только тогда, когда выполняется система
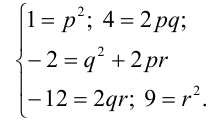
Ответ: 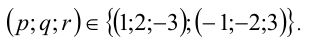
Теорема 6. Если значения двух многочленов степени не выше n совпадают в n + 1 различных точках, то эти многочлены тождественно равны.
Например, если две параболы (графики квадратичных функций 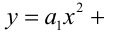
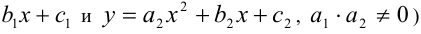 пересекаются в трёх точках, то они тождественно совпадают.
пересекаются в трёх точках, то они тождественно совпадают.
Теорема 7 (формула деления многочлена на многочлен с остатком). Для любых двух алгебраических многочленов
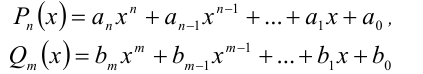
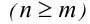 найдётся единственная пара многочленов
найдётся единственная пара многочленов 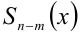 и
и 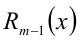 таких, что справедливо тождество
таких, что справедливо тождество
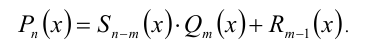
Здесь 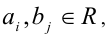
 , многочлен
, многочлен 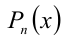 называется делимым, многочлен
называется делимым, многочлен 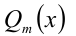 — делителем, многочлен
— делителем, многочлен 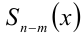 — частным от деления
— частным от деления 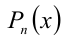 ) на
) на 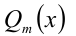 , а многочлен
, а многочлен 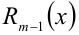 (степени не выше m — 1) соответственно остатком от деления. Если
(степени не выше m — 1) соответственно остатком от деления. Если 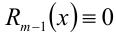 , то говорят, что многочлен
, то говорят, что многочлен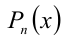 делится на многочлен
делится на многочлен 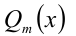 нацело (без остатка).
нацело (без остатка).
Пример №170.
Найти остаток от деления многочлена 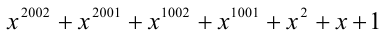 на многочлен
на многочлен 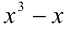 .
.
Решение:
В данной задаче весьма проблематично было бы искать многочлен-остаток непосредственным делением многочлена на многочлен из-за слишком высокой степени многочлена-делимого. Запишем результат деления первого многочлена на второй в виде формулы
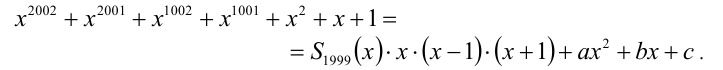
Здесь 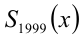 — неполное частное от деления (неизвестный многочлен), а остаток при делении на многочлен 3-й степени может иметь максимально 2-ю степень, поэтому остаток
— неполное частное от деления (неизвестный многочлен), а остаток при делении на многочлен 3-й степени может иметь максимально 2-ю степень, поэтому остаток 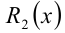 выписан в общем виде как многочлен 2-й степени
выписан в общем виде как многочлен 2-й степени 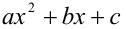 . Достаточно найти значения коэффициентов a,b и c . Для этого, подставляя последовательно значения x = 0, x = 1, x = — 1 в данную формулу, получим систему
. Достаточно найти значения коэффициентов a,b и c . Для этого, подставляя последовательно значения x = 0, x = 1, x = — 1 в данную формулу, получим систему
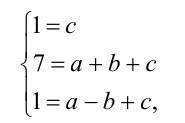
решая которую найдём искомые коэффициенты а = b = 3 , c = 1 . Поэтому остаток от деления равен 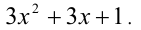
Следующая теорема названа по имени французского математика Этьена Безу (1730-1783).
Теорема 8 (теорема Безу). Остаток от деления многочлена 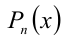 на
на 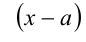 равен значению делимого при
равен значению делимого при 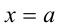 (т.е.
(т.е. 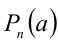 ).
).
Следствие. Многочлен 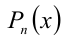 делится нацело на линейный двучлен
делится нацело на линейный двучлен 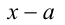 тогда и только тогда, когда
тогда и только тогда, когда 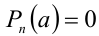 .
.
Приведённое следствие из теоремы Безу во многих случаях позволяет решать целые алгебраические уравнения 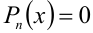 степени выше второй. Для этого достаточно подобрать один какой-либо корень уравнения, например
степени выше второй. Для этого достаточно подобрать один какой-либо корень уравнения, например 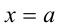 , и затем поделить многочлен
, и затем поделить многочлен 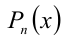 на
на 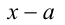 . В результате получим некоторый многочлен
. В результате получим некоторый многочлен 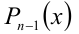 степени на единицу меньше, чем n :
степени на единицу меньше, чем n :
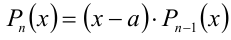 , и задача свелась к решению уравнения
, и задача свелась к решению уравнения
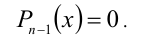
Пример №172.
Найти все значения а и b, при которых многочлен 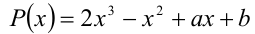 делится нацело на многочлен
делится нацело на многочлен 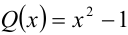 .
.
Решение:
Разложим многочлен 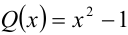 на линейные множители
на линейные множители 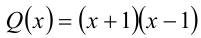 . По условию, Р(х) должен делиться на Q(х), а, следовательно, Р(х) должен делиться на каждый из множителей x + 1 и x — 1. Согласно теореме Безу, это возможно тогда и только тогда, когда
. По условию, Р(х) должен делиться на Q(х), а, следовательно, Р(х) должен делиться на каждый из множителей x + 1 и x — 1. Согласно теореме Безу, это возможно тогда и только тогда, когда
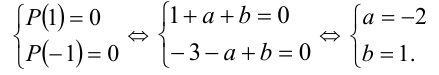
Теорема 9 (о рациональных корнях многочленов с целыми коэффи-циентами). Пусть 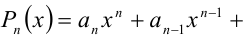
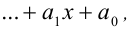
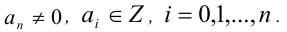 Если у многочлена
Если у многочлена 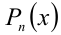 ) имеются рациональные корни, то все они находятся среди дробей вида p/q , где р — любой из целочисленных делителей свободного члена
) имеются рациональные корни, то все они находятся среди дробей вида p/q , где р — любой из целочисленных делителей свободного члена 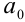 , a q — любой из натуральных делителей старшего коэффициента
, a q — любой из натуральных делителей старшего коэффициента 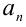 .
.
Следствие. Если 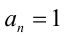 (приведённый многочлен), то его рациональные корни следует искать среди целых делителей
(приведённый многочлен), то его рациональные корни следует искать среди целых делителей 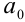 .
.
Пример №173.
Решить уравнение в целых числах
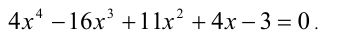
Решение:
Согласно следствию из приведённой выше теоремы, все целые корни уравнения находятся среди целых делителей свободного члена, т.е. среди чисел ± 1, ± 3 . Обозначим многочлен в левой части уравнения через f(x) . Сделаем проверку:
1) 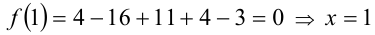 является корнем уравнения;
является корнем уравнения;
2) 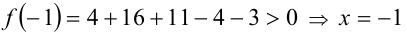 не будет корнем уравнения;
не будет корнем уравнения;
3)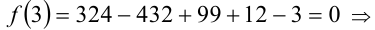 нашли ещё один корень x = 3 ;
нашли ещё один корень x = 3 ;
4) 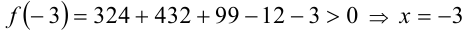 не является корнем.
не является корнем.
Ответ: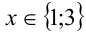 .
.
Пример №174.
Найти все корни уравнения 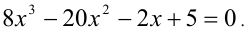
Решение:
Не будем сразу применять указанный выше метод, а поступим следующим образом: сделаем многочлен в левой части уравнения приведённым. Для этого положим у = 2х , тогда имеем уравнение
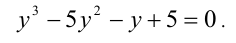
Обозначим через f(у) левую часть последнего уравнения. Свободный член в данном случае имеет 4 целых делителя ± 1, ± 5. Поскольку f( ± 1 )=0 и f(5)= 0, а больше трёх корней кубическое уравнение иметь не может, то это все корни этого уравнения. Выполняя обратную подстановку, находим соответствующие им три корня исходного уравнения.
Ответ: 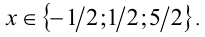
Обратимся теперь к обобщению теоремы Виета на случай алгебраических уравнений n -й степени 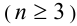 .
.
Теорема 10 (теорема Виета, общий случай). Пусть 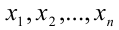 — действительные корни алгебраического многочлена n -й степени
— действительные корни алгебраического многочлена n -й степени
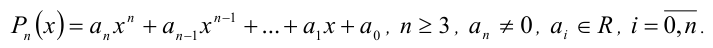
Тогда корни уравнения 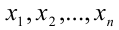 связаны с его коэффициента-ми
связаны с его коэффициента-ми 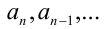
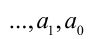 посредством следующей системы равенств:
посредством следующей системы равенств:
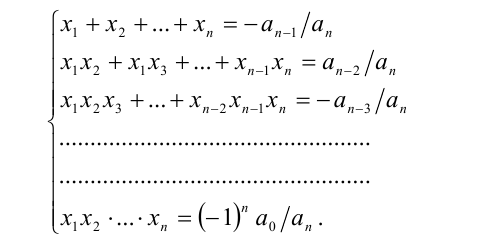
Пример №175.
Определить все значения параметра а, при каждом из которых три различных корня уравнения
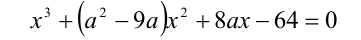
образуют геометрическую прогрессию. Найти эти корни.
Решение:
По теореме Виета для кубических уравнений
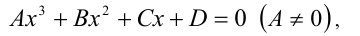
в частности, имеем 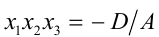 . Для данного в условии задачи уравнения это будет выглядеть так:
. Для данного в условии задачи уравнения это будет выглядеть так:

Условие того, что корни уравнения образуют геометрическую прогрессию, можно записать в виде

Из (1) и (2) следует, что 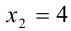 . Таким образом, известен один из корней уравнения. Подставив это значение x в исходное уравнение, найдём теперь отвечающие ему возможные значения параметра а :
. Таким образом, известен один из корней уравнения. Подставив это значение x в исходное уравнение, найдём теперь отвечающие ему возможные значения параметра а :
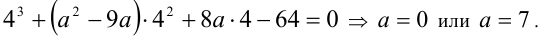
Проверка. 1) a = 0: исходное уравнение принимает вид 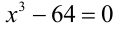 и, очевидно, имеет три одинаковых, а не различных корня. Следовательно, это значение параметра не подходит.
и, очевидно, имеет три одинаковых, а не различных корня. Следовательно, это значение параметра не подходит.
2) а = 1: имеем уравнение 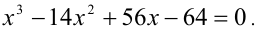 Так как один его корень нам известен (х = 4), то, например, делением многочлена в левой части на х — 4 раскладываем многочлен на множители, приведя уравнение к виду
Так как один его корень нам известен (х = 4), то, например, делением многочлена в левой части на х — 4 раскладываем многочлен на множители, приведя уравнение к виду
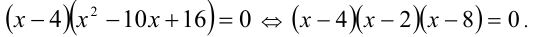
Его корни 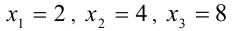 удовлетворяют условиям задачи.
удовлетворяют условиям задачи.
Ответ: 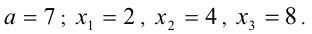
А теперь обратимся к рассмотрению основных видов и способов решения целых алгебраических уравнений.
Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:
Эти страницы возможно вам будут полезны:

