Оглавление:
Примеры неравносильных преобразований
Рассмотрим несколько преобразований, приводящих к следствию (чтобы такого рода преобразования стали равносильными, в большинстве случаев надо просто учесть ОДЗ в решаемой задаче).
1.Возведение уравнения вида f(x)=g(x) в чётную степень приводит, вообще говоря, к следствию:
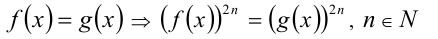
(в последнем уравнении f (х) и g (x) могут иметь разные знаки).
2.Умножение уравнения вида 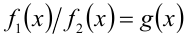 на функцию, стоящую в знаменателе, приводит, вообще говоря, к следствию (снимается ограничение
на функцию, стоящую в знаменателе, приводит, вообще говоря, к следствию (снимается ограничение 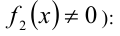
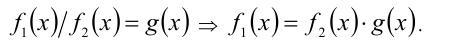
3.Взаимное уничтожение одного и того же слагаемого-функции в обеих частях уравнения приводит, вообще говоря, к следствию (из-за возможного расширения ОДЗ):
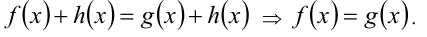
4.Переход от уравнения вида 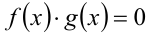 к совокупности уравнений приводит, вообще говоря, к следствию:
к совокупности уравнений приводит, вообще говоря, к следствию:
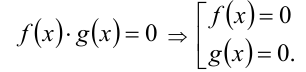
Например,
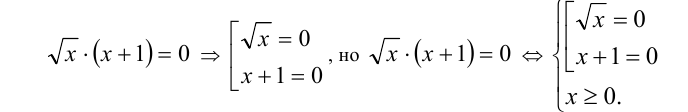
5.Возведение иррациональных уравнений вида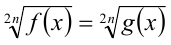 в чётную степень 2n с целью избавления от радикалов приводит, вообще говоря, к следствию (снимаются ограничения
в чётную степень 2n с целью избавления от радикалов приводит, вообще говоря, к следствию (снимаются ограничения 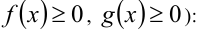
6.В следующей цепочке преобразований происходит постепенное расширение ОДЗ, что, вообще говоря, может привести к появлению посторонних корней.
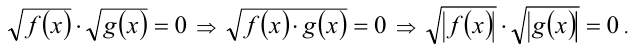
7.Применение операции взятия синуса к обеим частям уравнения приводит к следствию:
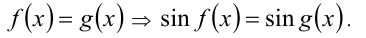
Например,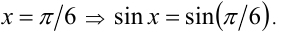
Замечание 1. Понятия равносильности, следствия распространяются на неравенства, системы и совокупности уравнений и неравенств.
Замечание 2. Некорректное использование в процессе решения уравнения соотношения, эквивалентного данному уравнению, вопреки расхожему мнению, может повлечь появление посторонних корней.
Пример №143.
Найти все решения иррационального уравнения вида
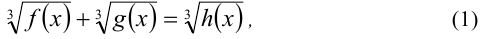
где f(х), g(x),h(х) — рациональные функции, определённые при всех действительных x.
Решение:
Обозначим 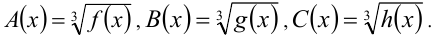 Тогда уравнение (1) примет вид
Тогда уравнение (1) примет вид

что равносильно
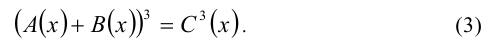
Уравнение (3) преобразуем с учётом уравнения (1), записанного в виде равенства (2), и получим равенство
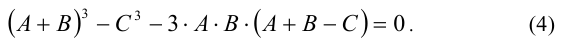
Воспользовавшись формулами сокращенного умножения, разложим левую часть последнего равенства в произведение
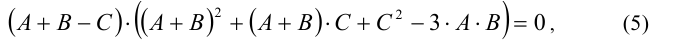
что эквивалентно совокупности двух уравнений
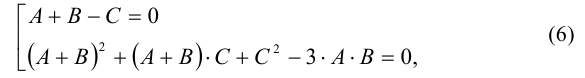
причём второе из уравнений приводится к эквивалентному виду
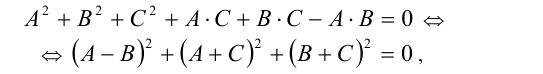
что, в свою очередь, равносильно системе А(х)=В(х) = -С(х). (7)
Если система уравнений (7) имеет корни, не совпадающие с корнями данного уравнения (2), то это — посторонние корни; если же эта система не имеет корней, то посторонних корней нет.
Проанализируем, за счёт чего здесь возникли посторонние корни. В самом деле, при переходе от уравнения (2) к равенству (5) предполагается, что А + В — С = 0 . Поэтому, строго говоря, уравнение (5), а также совокупность (6) необходимо дополнить этим условием. Например, совокупность (6) на самом деле должна иметь вид
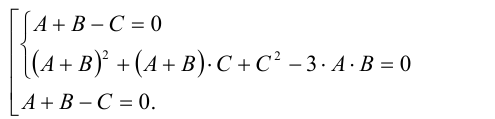
Другими словами, при правильном решении дополнительных корней появиться не может. Рассмотрим конкретный пример.
Пример №144.
Решить уравнение 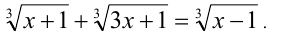
.
Решение:
Данное уравнение — иррациональное, определённое при всех действительных значениях x . Введём обозначения
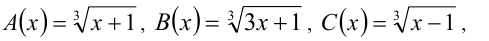
и перепишем исходное уравнение в виде A(х) + В(х) = С(х), который после возведения в куб эквивалентен уравнению
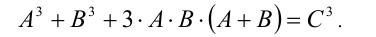
Заменяя А + В на С (в этот момент возможно возникновение посторонних корней), получаем
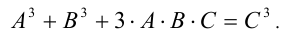
Возвращаясь в последнем уравнении к переменной x, имеем
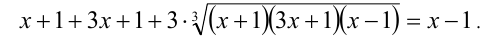
Осталось решить это уравнение. Приведём подобные члены, уединив кубический корень
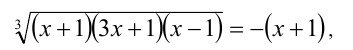
и после этого возведём в куб
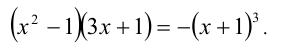
У этого кубического уравнения два корня: —1 и 0. Проверка (которую сделать необходимо!) показывает, что x = 0 — посторонний корень, поскольку не удовлетворяет исходному уравнению. Заметим, что он удовлетворяет системе (7), которая в данном примере имеет вид
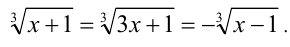
Ответ: 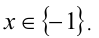
Пример №145.
Равносильны ли уравнения 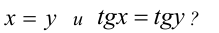
Решение:
Заметим, что пара чисел 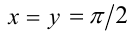 удовлетворяет первому из уравнений, но не может быть решением второго уравнения, поскольку не принадлежит его ОДЗ. С другой стороны, пара чисел
удовлетворяет первому из уравнений, но не может быть решением второго уравнения, поскольку не принадлежит его ОДЗ. С другой стороны, пара чисел 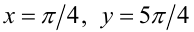 удовлетворяет второму уравнению, так как в этом случае tgx = tgy = 1, но в то же время эта пара, очевидно, не является решением первого уравнения. Данное наблюдение позволяет утверждать, что данные два уравнения не сравнимы между собой (в том числе не являются равносильными).
удовлетворяет второму уравнению, так как в этом случае tgx = tgy = 1, но в то же время эта пара, очевидно, не является решением первого уравнения. Данное наблюдение позволяет утверждать, что данные два уравнения не сравнимы между собой (в том числе не являются равносильными).
Пример №146.
При каких значениях параметра а неравенство

является следствием неравенства

Решение:
Решением второго из неравенств является интервал (1,3). Так как при любом значении параметра число а лежит на числовой прямой левее числа а + 2, то решением первого неравенства является объединение двух промежутков 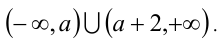 Чтобы выполнялось условие задачи, множество
Чтобы выполнялось условие задачи, множество 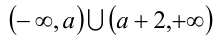 должно содержать внутри себя интервал (1, 3). Возможны два случая.
должно содержать внутри себя интервал (1, 3). Возможны два случая.
1) Интервал (1, 3 ) целиком принадлежит интервалу 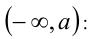

Чтобы это выполнялось, необходимо потребовать 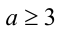 .
.
2) Интервал (1, 3) целиком принадлежит интервалу 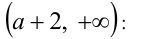

В этом случае должно выполняться условие 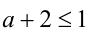 . Объединяя полученные значения параметра, приходим к ответу.
. Объединяя полученные значения параметра, приходим к ответу.
Ответ: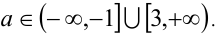
Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:
Эти страницы возможно вам будут полезны:

