Оглавление:
Примеры равносильных преобразований
1.Возведение уравнения (неравенства) в нечётную натуральную степень (извлечение алгебраического корня нечётной степени) приводит к равносильному уравнению (неравенству):
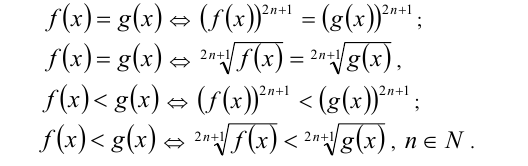
Пример №141.
Решить уравнение
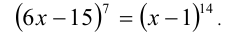
Решение:
Извлекая корень седьмой степени, приходим к равносильному уравнению
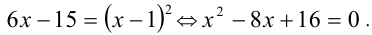
Ответ: 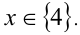
Если функции f (х) и g(x) неотрицательны на некотором множестве, то на этом множестве равносильны уравнения (неравенства):
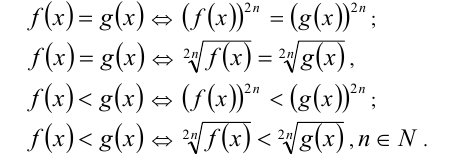
Если функция h(x) определена на ОДЗ исходного уравнения (неравенства), то её можно прибавлять (вычитать) к обеим частям уравнения (неравенства):
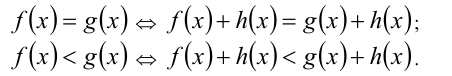
В частности, к обеим частям уравнения (неравенства) можно прибавлять (вычитать) одно и то же действительное число а :
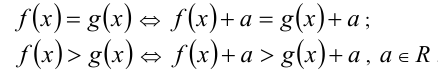
Если же функция h(х) определена не при всех 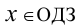 исходного уравнения (т.е. ОДЗ функции h(х) уже), то добавление функции h(х) к обеим частям уравнения может привести к потере решений, например:
исходного уравнения (т.е. ОДЗ функции h(х) уже), то добавление функции h(х) к обеим частям уравнения может привести к потере решений, например:
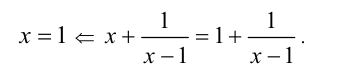
Если функция h(x) определена и не обращается в нуль на ОДЗ исходного уравнения, то обе части уравнения можно одновременно умножать (делить) на эту функцию:
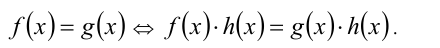
В частности, обе части уравнения можно умножать (делить) на одно и то же отличное от нуля действительное число а :
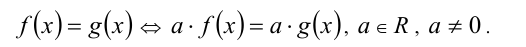
Например, если в уравнении вида 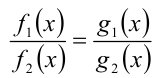 функции, стоящие в знаменателях дробей, не обращаются в нуль
функции, стоящие в знаменателях дробей, не обращаются в нуль 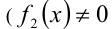 и
и 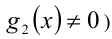 на ОДЗ
на ОДЗ
уравнения, то такое урансние равносильно уравнению, полученному в результате перемножения крайних и средних членов этой пропорции:
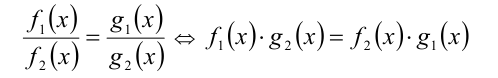
(для доказательства достаточно умножить обе части данного уравнения на произведение знаменателей 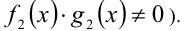 В общем случае, если снять ограничения
В общем случае, если снять ограничения 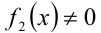 и
и 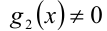 , это будет переход к следствию.
, это будет переход к следствию.
Если же функция h(x) имеет свои корни на ОДЗ исходного уравнения, то умножение на h(x) приводит к следствию, причём посторонними корнями будут как раз корни уравнения 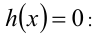
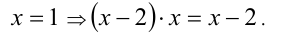
Если h(х) определена не на всей ОДЗ исходного уравнения (её ОДЗ>’же), то при умножении на h(x) может произойти потеря корней или даже уравнения могут оказаться несравнимыми.
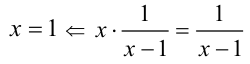 — (потеря единственного корня);
— (потеря единственного корня);
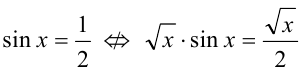 — (уравнения не сравнимы).
— (уравнения не сравнимы).
Если функция h(x) определена и положительна на ОДЗ неравенства, то обе его части можно одновременно умножать (делить) на эту функцию, при этом знак неравенства сохраняется:
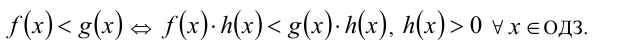
В частности, обе части неравенства можно умножать (делить) на одно и то же положительное действительное число:
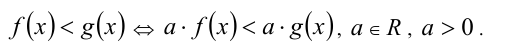
Например, в строгих неравенствах вида 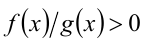 множитель g(x) из знаменателя дроби можно «переносить» в числитель:
множитель g(x) из знаменателя дроби можно «переносить» в числитель:
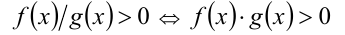
(для доказательства достаточно умножить обе части исходного неравенства на 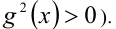
Если функция h(x) определена и отрицательна на ОДЗ неравенства, то обе его части можно одновременно умножать (делить) на эту функцию, при этом знак неравенства следует поменять на противоположный:
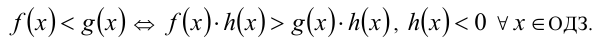
В частности, обе части неравенства можно умножать (делить) на одно и то же отрицательное действительное число:
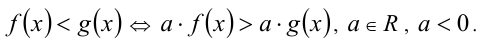
Показательные уравнения вида 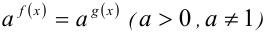
равносильны уравнению, полученному в результате логарифмирования:
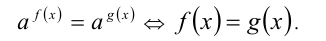
Если из уравнения 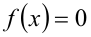 следует уравнение
следует уравнение 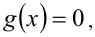 то
то
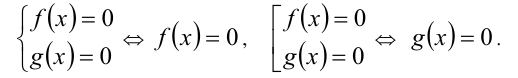
Пример №142.
Решить уравнение
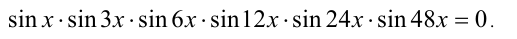
Решение:
Данное уравнение равносильно на множестве действительных чисел совокупности шести уравнений
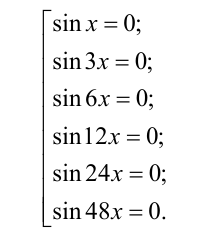
Перенумеруем уравнения цифрами (l)-(6). При этом если sinx = 0, то по формуле синуса тройного аргумента получаем, что sin3x = 0 Далее, если sin 3x = 0, то по формуле синуса двойного аргумента получаем, что sin 6x = 0, и так далее. Таким образом, каждое последующее уравнение в совокупности является следствием своего предшественника, а значит уравнение (6) является следствием уравнений (1)-(5):
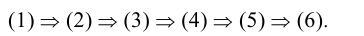
Поэтому данная совокупность оказывается равносильной уравнению (6): sin48x = 0. решая которое, находим 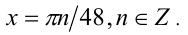
Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:
Эти страницы возможно вам будут полезны:

