Задачи на доказательство различных алгебраических неравенств
Существуют конкурсные задачи, в которых требуется доказать справедливость того или иного алгебраического неравенства, в записи которого присутствуют несколько буквенных обозначений, при всех значениях входящих в него букв (доказательство тождеств) или, например, только для положительных значений. Иногда требуется доказать неравенство при выполнении некоторого дополнительного условия. Рассмотрим примеры.
Пример 1. Доказать, что при всех действительных а,vb, c имеет место неравенство
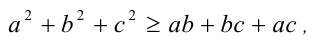
и выяснить, когда оно обращается в равенство.
Доказательство. Выполним следующие равносильные преобразования:
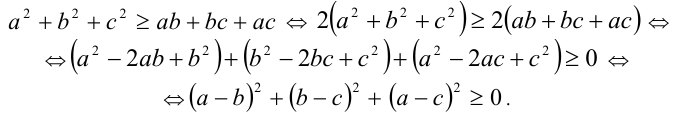
Последнее неравенство, очевидно, выполняется при всех действительных значениях а,b,c. при этом обращается в равенство тогда и только тогда, когда все три квадрата равны нулю, т.е. а = b = c .
Пример 2 . Три положительных числа a,b,c таковы, что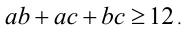 
Доказать, что в этом случае имеет место неравенств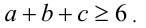 
Доказательство. Воспользуемся доказанным выше неравенством:
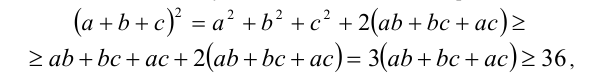
откуда и получим, что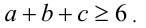
Пример 3 . Пусть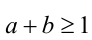 
. Доказать справедливость неравенства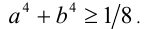 
Доказательство. Так как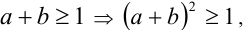 
т.е.
Сложив это неравенство с известным неравенством
получим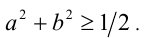 
Аналогично, так как 
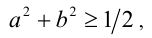то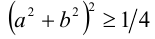 
, т.е.
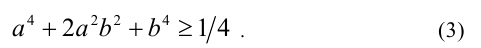
Сложив неравенство (3) с неравенством
получим искомое неравенство.
Приведём теперь пример задачи, в которой для повышения эффективности решения целесообразно использовать замену переменных.
Пример 4 . Доказать, что если а > 0, b > 0 , c>0, то
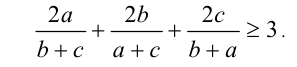
Доказательство. Пусть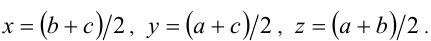 
Тогда, выражая а,b,с через x,y,z, получим систему
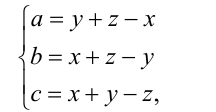
и доказываемое неравенство принимает вид
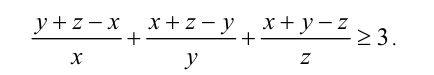
Поделив почленно и сгруппировав слагаемые, получим
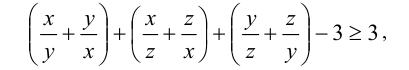
что, очевидно, верно (в силу неравенства о сумме взаимно обратных положительных чисел). Неравенство доказано.
Пример 5 . Пусть а + b = 2 . Доказать, что
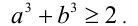
Доказательство. Так как а + b = 2 , то найдётся такое числ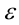о 
, что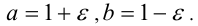 
Тогда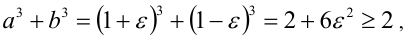 
что и требовалось доказать.
Пример 6. Пусть а > c > 0, b > С. Доказать, что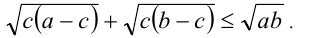 
Доказательство. Положим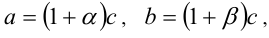 
где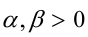 
Надо доказать, что
Имеем: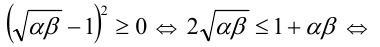 
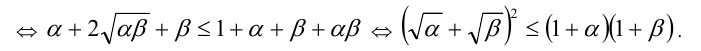
Последнее неравенство обращается в равенство тогда и только тогда, когда
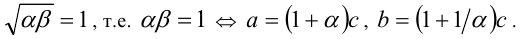
Исключая из этой системы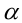 
, находим условие обращения неравенства в равенство: 
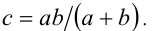В следующем примере показывается, что иногда неравенство можно доказать с помощью геометрического подхода.
Пример 7. Доказать, что для любых положительных чисел а,b,c справедливо неравенство
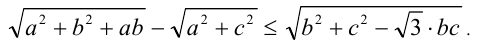
Доказательство. Известно, что для треугольника со сторонами а,b,c и углом величины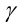 
между сторонами а,b справедлива теорема косинусов:
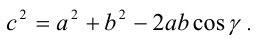
Запишем выражение под первым из радикалов в виде:
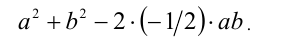
Тогда геометрический смысл этого радикала состоит в том, что он численно равен длине третьей стороны АВ в треугольнике ОАВ со сторонами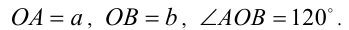 
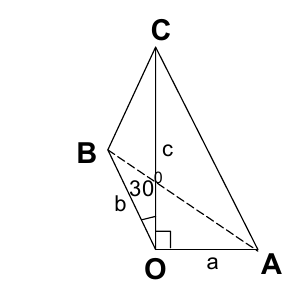
Аналогично можно дать геометрическую интерпретацию двум другим радикалам в исходном неравенстве:
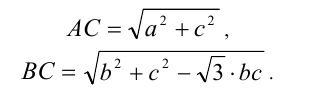
В результате неравенство принимает вид:
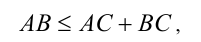
что, очевидно, верно, так как это известное из геометрии неравен-ство треугольника (справедливо при произвольном расположении точек А, В, С на плоскости).
Задачи, при решении которых для более быстрого (по сравнению со стандартными способами) получения тех или иных оценок используются алгебраические неравенства, часто относят к нестандартным. Задачи такого рода периодически встречаются на олимпиадах и при выполнении тестов по математике. Формирование навыков использования при оценивании исследуе-мых величин подходящих неравенств, безусловно, повышает общую культуру школьника.
Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:
Эти страницы возможно вам будут полезны:
