Оглавление:
Неравенство Коши
Коши Огюстен Луи (1789—1857) — французский математик, работавший главным образом в области математического анализа (дифференциальные уравнения, теория рядов) и теории функций комплексного переменного. Член Парижской Академии наук. Написал за свою жизнь около 1500 научных работ.
Вначале докажем вспомогательную лемму.
Лемма. Если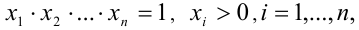 
то
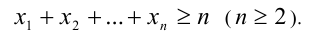
Доказательство. Воспользуемся методом математической индукции. 1) Убедимся в справедливости данного утверждения при n = 2 :
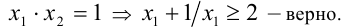
Причём равенство достигается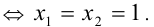 
2) Предположим, что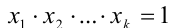 
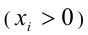и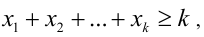 
и рассмотрим любые положительные числа 
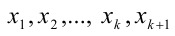такие, что 
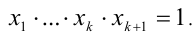Если все эти числа равны единице, то доказываемое утверждение очевидно. Пусть это не так. Тогда среди этих чисел найдётся число, меньшее 1, и число, большее 1. Допустим, что 
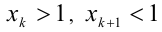(можно было наоборот). Имеем равенство:
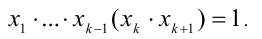
К этому произведению k чисел применимо предположение индукции, т.е.
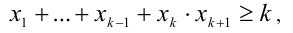
откуда получаем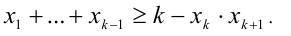 
Но тогда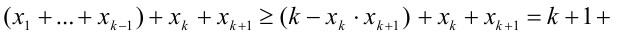 
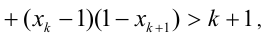так как 
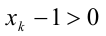и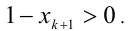 
При этом равенство достигается 
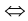все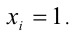 
.
3) В силу произвольности k , лемма доказана.
А теперь докажем неравенство между средним арифметическим и средним геометрическим в общем случае (для n чисел).
Теорема (неравенство Коши). Для любых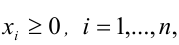 
, справедливо неравенство
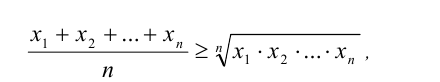
которое обращается в равенство тогда и только тогда, когда
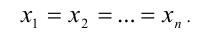
Доказательство. Обозначим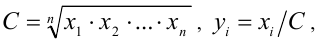 
и применим лемму для чисел 
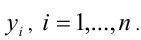Так как 
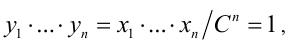то, по доказанному выше,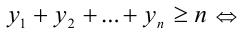 
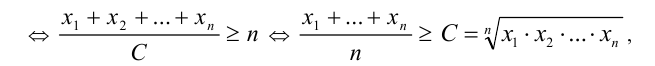
причём неравенство обращается в равенство, только когда все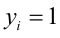 
, т.е.
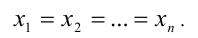
Пример №131.
Доказать неравенства Коши:
- для четырёх чисел
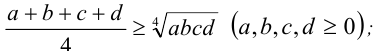
2) для трёх чисел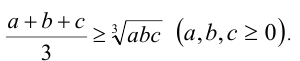 
Доказательство. Рассмотрим доказательство указанных неравенств без использования общего неравенства Коши. Докажем вначале неравенство для четырёх чисел, а уже потом с его помощью для трёх чисел.
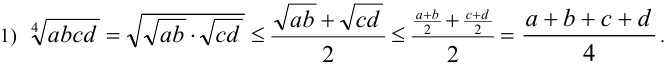
2) Запишем неравенство Коши для четырёх чисел а,b,c и (а + b + с)/3:
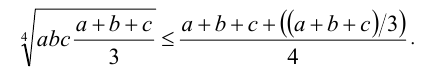
Упростив правую часть, возведём неравенство в четвёртую степень. Сокращая на (а + b + с)/3 и извлекая кубический корень, получим требуемое.
Пример №132.
Сравнить два числа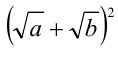 
и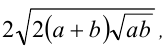 
где а и b —неотрицательные числа,
.
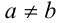Решение:
Преобразуем числа к виду
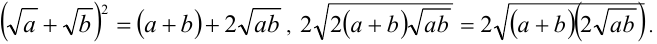
После деления обоих чисел на 2, приходим к неравенству между средними арифметическим и геометрическим (для чисел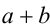 
и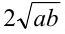 
):
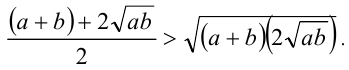Ответ: первое число больше.
Пример №133.
Доказать, что верно неравенство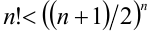 
, где n —любое целое число, большее единицы.
Решение:
Запишем неравенство Коши для чисел 1, 2, 3,…, n :
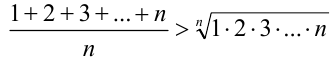
(знак в неравенстве строгий, так как все числа различны). Упрощая левую часть по формуле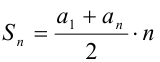 
суммы первых n членов арифметической прогрессии 
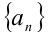с первым членом 
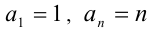, и заменяя справа подкоренное выражение на n!, получим 
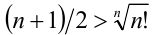, откуда, возводя обе части неравенства в степень n , получаем искомое неравенство доказанным.
Пример №134.
Найти наименьшее значение функции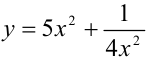
.
Решение:
При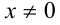 
воспользуемся для решения задачи следствием неравенства Коши: 
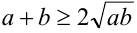, положив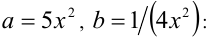
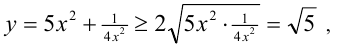
причём наименьшее значение функции, равное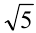 
, достигается тогда и только тогда, когда 
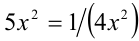, т.е. при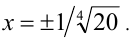 
Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:
Эти страницы возможно вам будут полезны:
