Оглавление:
Понятие n-факторнала. Бином Ньютона. Биномиальные коэффициенты. Треугольник Паскаля
Произведение всех натуральных чисел, начиная с единицы и заканчивая n, называется n —факториалом и обозначается n!, т.е.
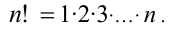
По определению полагают 0!=1, 1!= 1 . Например,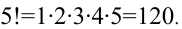 Задачи на факториалы достаточно редко, но всё же встречаются на вступительных экзаменах.
Задачи на факториалы достаточно редко, но всё же встречаются на вступительных экзаменах.
Пример №124.
Сколькими нулями оканчивается число 2000!?
Рассмотрим решение этой достаточно известной задачи. Предположим, что мы разложили данное большое число 2000! на простые множители (в силу основной теоремы арифметики это можно сделать, причём единственным образом):
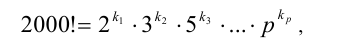
где показатели степеней 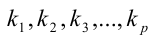
— некоторые неизвестные нам натуральные числа. Нуль будут давать только произведения пар простых множителей 2 и 5. В этом разложении 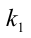 двоек и
двоек и 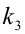 пятёрок, причём каждое второе число в натуральном ряду чисел кратно двум и только каждое пятое кратно пяти. Следовательно,
пятёрок, причём каждое второе число в натуральном ряду чисел кратно двум и только каждое пятое кратно пяти. Следовательно, 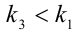 . Поэтому число нулей будет равно
. Поэтому число нулей будет равно 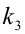 . Найдём это число. Среди чисел 1,2,3, …,1999,2000 каждое пятое делится на 5. Таких чисел
. Найдём это число. Среди чисел 1,2,3, …,1999,2000 каждое пятое делится на 5. Таких чисел 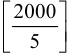 штук (квадратные скобки обозначают целую часть). Далее, каждое 25-е число делится еще на пять, и таких чисел
штук (квадратные скобки обозначают целую часть). Далее, каждое 25-е число делится еще на пять, и таких чисел 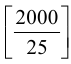 штук. Затем каждое 125-е число делится ещё на пять, и таких пятёрок будет
штук. Затем каждое 125-е число делится ещё на пять, и таких пятёрок будет 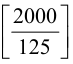 штук. Продолжая этот конечный процесс (начиная с определённого момента целая часть будет обращаться в нуль), получим в результате
штук. Продолжая этот конечный процесс (начиная с определённого момента целая часть будет обращаться в нуль), получим в результате
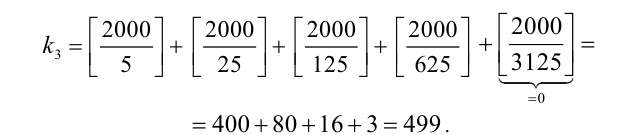
Ответ: 499 нулями.
Пример №125.
Найти значение выражения
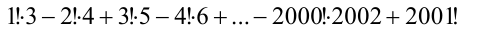
Решение:
Заметим, что каждое слагаемое в приведённой сумме, кроме последнего, имеет вид 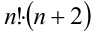 , где n изменяется от значения 1 (у первого члена суммы) до 2000 (у предпоследнего слагаемого). Поскольку
, где n изменяется от значения 1 (у первого члена суммы) до 2000 (у предпоследнего слагаемого). Поскольку 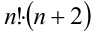 можно представить в виде
можно представить в виде 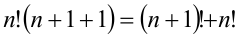 , то, заменяя каждое из слагаемых (кроме последнего) на соответствующую сумму, получим:
, то, заменяя каждое из слагаемых (кроме последнего) на соответствующую сумму, получим:
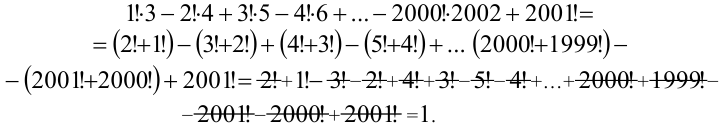
Ответ: 1.
Пример №126.
Вычислить сумму
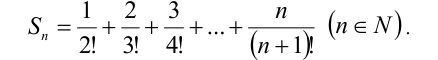
Решение:
Воспользуемся тождеством
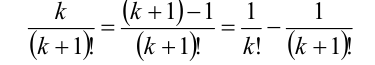
для каждого из слагаемых (k = 1,2,…,n). Тогда имеем
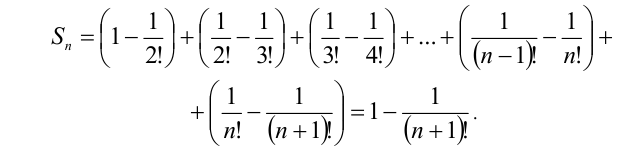
Пример №127.
Решить в целых числах уравнение
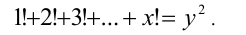
Решение:
Непосредственной проверкой убеждаемся, что при x < 5 решениями уравнения будут пары чисел (l;±l), (3;±3). Докажем теперь, что при 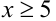 решений нет. Для этого заметим, что 1!+2!+3!+4!= 33 оканчивается цифрой 3, а 5!,6!,7!,…— все оканчиваются нулём. Таким образом, при
решений нет. Для этого заметим, что 1!+2!+3!+4!= 33 оканчивается цифрой 3, а 5!,6!,7!,…— все оканчиваются нулём. Таким образом, при 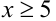 сумма
сумма 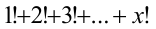 оканчи-вается цифрой 3, а потому не может равняться квадрату целого числа у (никакой квадрат целого числа не оканчивается на 3).
оканчи-вается цифрой 3, а потому не может равняться квадрату целого числа у (никакой квадрат целого числа не оканчивается на 3).
Наряду с понятием обычного, или одинарного, факториала существует понятие двойного факториала. Приведём для любознательных читателей соответствующее определение. Произведение всех натуральных чисел, начиная с единицы и заканчивая n, имеющих одинаковую с n чётность, называется двойным n —факториалом и обозначается n!!
В частности, если 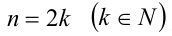 , то
, то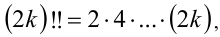 а если
а если 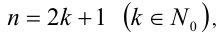 то
то 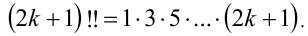 По определению полагают 0!!= 1. Например, 1!!=1, 2!!=2, 8!!= 2 • 4 • 6 • 8 = 384, 7!! = 1 • 3 • 5 • 7 = 105. Справедливо тождество n!= n!!•(n — 1)!!.
По определению полагают 0!!= 1. Например, 1!!=1, 2!!=2, 8!!= 2 • 4 • 6 • 8 = 384, 7!! = 1 • 3 • 5 • 7 = 105. Справедливо тождество n!= n!!•(n — 1)!!.
Пример №128.
В какой степени входит число 2 в разложение на произведение степеней простых чисел следующего выражения:
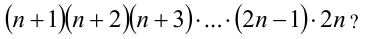
Решение:
Преобразуем данное выражение:
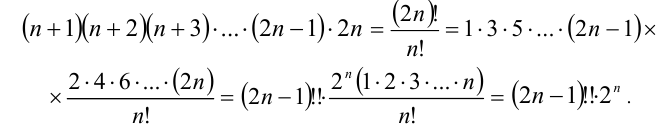
Так как первый из двух сомножителей является нечётным числом, то двойка входит в каноническое разложение в степени, равной n.
Комбинаторика — это раздел математики, изучающий количество комбинаций, которые можно составить из заданного конечного множества 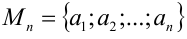 попарно различных элементов произвольной природы. Основным правилом комбинаторики является принимаемое без доказательства правило умножения: если объект А может быть выбран из заданного множества
попарно различных элементов произвольной природы. Основным правилом комбинаторики является принимаемое без доказательства правило умножения: если объект А может быть выбран из заданного множества 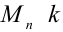 спосо-бами и при каждом выборе объекта А другой объект В может быть выбран mспособами, то объект, состоящий из объединения А и В , может быть выбран k• m способами.
спосо-бами и при каждом выборе объекта А другой объект В может быть выбран mспособами, то объект, состоящий из объединения А и В , может быть выбран k• m способами.
Пример №129.
Сколько различных целых делителей имеет число 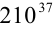 ?
?
Решение:
Поскольку 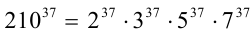 , то, следовательно, делителями этого числа являются числа вида
, то, следовательно, делителями этого числа являются числа вида
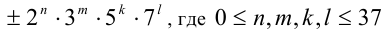
Таким образом, искомое количество делителей равно 2 • (число различных наборов 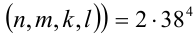
Рассмотрим вопрос из области комбинаторики: сколькими способами можно выбрать m предметов из n различных предметов? Количество таких способов принято обозначать 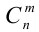 и называть числом сочетаний из n по m . Число сочетаний из n по m можно вычислить по следующей формуле, в написании которой используется понятие факториала:
и называть числом сочетаний из n по m . Число сочетаний из n по m можно вычислить по следующей формуле, в написании которой используется понятие факториала:
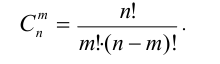
Например,
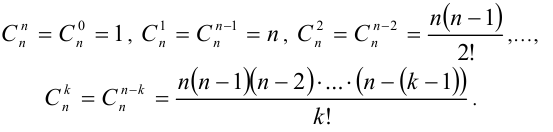
Кстати, число n! в комбинаторике также имеет свой смысл. Количество различных способов, какими можно упорядочить n данных предметов, называется числом перестановок из n предметов,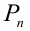
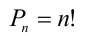
К разряду формул сокращённого умножения принято относить и бином Ньютона. Пусть а и b — произвольные действительные числа, n — любое натуральное число. Биномом Ньютона называется следующая формула для вычисления 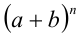 (доказывается в разделе 4):
(доказывается в разделе 4):
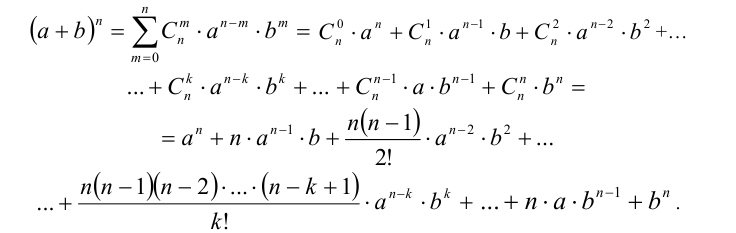
Здесь числа 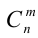 называются биномиальными коэффициентами.
называются биномиальными коэффициентами.
Формула бинома Ньютона была известна математикам задолго до Ньютона. Заслуга И.Ньютона в том, что он сумел получить гораздо более общую формулу — для степени 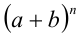 , где n — любое действительное число.
, где n — любое действительное число.
Коэффициенты 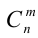 могут быть последовательно записаны в так называемый треугольник Паскаля (в котором каждое число внутри треугольника равно сумме двух чисел, стоящих над ним):
могут быть последовательно записаны в так называемый треугольник Паскаля (в котором каждое число внутри треугольника равно сумме двух чисел, стоящих над ним):
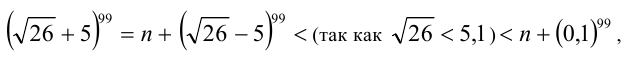
откуда и следует доказываемый результат.
В заключение данного пункта рассмотрим пример текстовой задачи, при решении которой понадобится обычная практическая логика и немного правило умножения (из комбинаторики).
Пример №130.
Сколько времени в течение суток на электронном табло вокзальных часов, которые показывают время в диапазоне от 00:00 до 23:59, присутствует хотя бы одна цифра 3?
Решение:
Занумеруем четыре позиции табло слева направо. В 1-й позиции цифра «3» не появляется никогда. Во 2-й позиции цифра «3» присутствует в течение трёх полных часов, начинающихся с 03:00, 13:00, 23:00. Остаётся 21 час, в течение каждого из которых цифра «3» по одному разу занимает 3-ю позицию табло в течение 10 минут, а в течение остальных 50 минут каждого часа 5 раз ровно 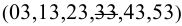 по 1 минуте занимает последнюю, 4-ю позицию табло.
по 1 минуте занимает последнюю, 4-ю позицию табло.
В результате общее время присутствия цифры «3» на табло равно
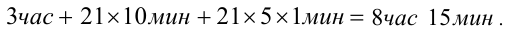
Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:
Эти страницы возможно вам будут полезны:

