Оглавление:
Числовые неравенства и их свойства
Обратим внимание на то обстоятельство, что понятие неравенства, вообще говоря, можно ввести только на упорядоченном числовом множестве, например на множестве действительных чисел.
Если два действительных числа а и b соединены одним из знаков неравенств: 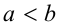 , или
, или 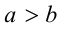 , или
, или 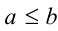 , или
, или 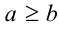 , или
, или 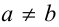 , то говорят, что задано числовое неравенство. При этом неравенства
, то говорят, что задано числовое неравенство. При этом неравенства 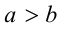 и
и 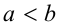 называются строгими, а неравенства
называются строгими, а неравенства 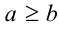 и
и 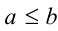 — нестрогими. Числовое неравенство может быть верным либо неверным.
— нестрогими. Числовое неравенство может быть верным либо неверным.
Ниже при доказательстве свойств числовых неравенств наряду с законами коммутативности, ассоциативности, дистрибутивности и утверждениями 1, 2, 3 мы будем использовать (без доказательства) также три следующих утверждения, вытекающие из определения арифметических операций суммы и произведения двух действительных чисел, понятия противоположных (по знаку) чисел, а также операции сравнения действительных чисел.
Утв. 4. Сумма двух положительных чисел положительна.
Утв. 5. Произведение двух положительных чисел положительно.
Утв. 6. Если 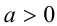 , то
, то 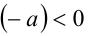 ; если
; если 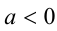 , то
, то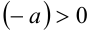 .
.
Свойства числовых неравенств
Пусть а ,b, c ,d — произвольные действительные числа. Приведённые ниже свойства сформулированы для строгих и нестрогих неравенств, но доказываются только для случая строгих неравенств.
1. Одно из двух чисел больше второго тогда и только тогда, когда второе число меньше первого:
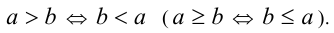
2. Если одно число больше второго, а второе число больше третьего, то первое число больше третьего (транзитивность неравенств):
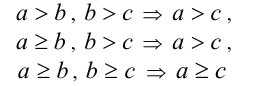
(последнее неравенство обращается в равенство 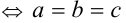 ).
).
3.К обеим частям неравенства можно прибавлять (вычитать) одно и то же число, при этом знак неравенства сохраняется:
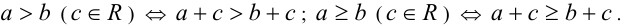
1.а) Обе части неравенства можно умножать (делить) на одно и то же положительное число, при этом знак неравенства сохраняется:
если 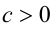 , то
, то 
б) Обе части неравенства можно умножать (делить) на одно и то же отрицательное число, при этом знак неравенства меняется на противоположный:
если 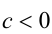 , то
, то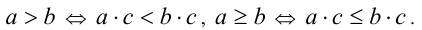
5.Неравенства одного знака можно почленно складывать:
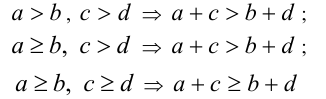
(последнее неравенство обращается в равенство тогда и только тогда, когда одновременно а = b и с = d ).
6.Неравенства одного знака с положительными (неотрицательными) членами можно почленно перемножать:
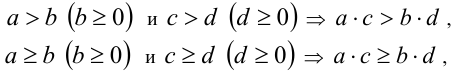
(последнее неравенство обращается в равенство тогда и только тогда, когда одновременно а = b и с = d ).
Если перемножаются нестрогое неравенство со строгим, то в результате может получиться как строгое неравенство:
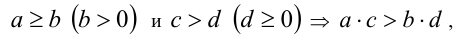
так и нестрогое неравенство:
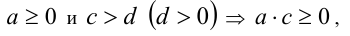
(последнее неравенство обращается в равенство 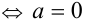 ).
).
7.а) Число, обратное к положительному (отрицательному) числу, положительно (отрицательно):
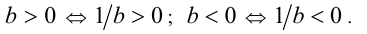
б) Числа, обратные к двум числам одного знака, связаны неравенством противоположного знака:
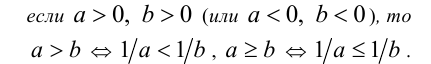
Следствие. 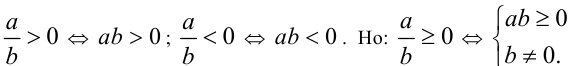
8.а) Если обе части неравенства положительны, то при возведении его в любую натуральную степень n (т.е. умножении самого на себя n раз) знак неравенства сохраняется:
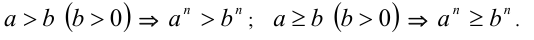
Сформулированное свойство можно усилить:
б) если 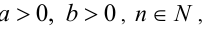 то
то
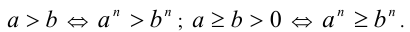
в) если n — нечётно, то при любых 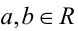 верно утверждение:
верно утверждение:
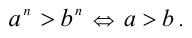
Следствие. Для любого положительного числа а и любого натурального числа n неравенство а > 1 выполняется тогда и только тогда, когда выполняется неравенство 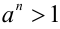 .
.
Доказательство.
Докажем, что  . Согласно утверждению 2,
. Согласно утверждению 2, 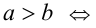
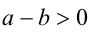 . По утверждению 6,
. По утверждению 6, 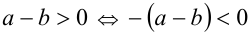 В соответствии с законом дистрибутивности раскроем скобки:
В соответствии с законом дистрибутивности раскроем скобки: 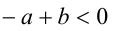 , а в соответствии с
, а в соответствии с
законом коммутативности поменяем слагаемые местами: 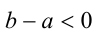 . Согласно утверждению 3, последнее неравенство равносильно тому, что b < а .
. Согласно утверждению 3, последнее неравенство равносильно тому, что b < а .
Докажем, например, что если а > b и b > c, то а > c . Согласно утвер-ждению 2, имеем: 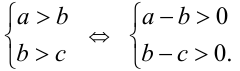 Поскольку
Поскольку 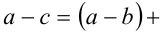
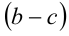 , и, согласно утверждению 4,
, и, согласно утверждению 4, 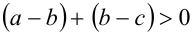 , то
, то 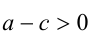 . Наконец, по утверждению 2,
. Наконец, по утверждению 2, 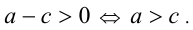
Докажем, что при любом c равносильны неравенства а > b и а +c> b +c . Согласно утверждению 2,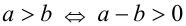 . Поскольку, используя закон ассоциативности сложения,
. Поскольку, используя закон ассоциативности сложения, 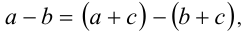 то
то 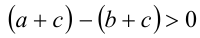 . Согласно утверждению 2,
. Согласно утверждению 2, 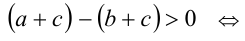
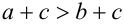 .
.
а) Докажем, что если c > 0 , то неравенства а > b и 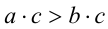 равносильны.
равносильны.
Необходимость. Пусть а > b , и требуется доказать, что 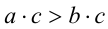 . Во-первых, согласно утверждению 2,
. Во-первых, согласно утверждению 2, 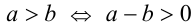 . Во-вторых, согласно утверждению 5,
. Во-вторых, согласно утверждению 5, 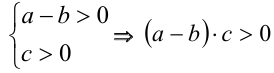 . Согласно распределительному закону, раскроем в последнем неравенстве скобки:
. Согласно распределительному закону, раскроем в последнем неравенстве скобки: 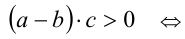
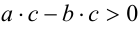 . Наконец, согласно утверждению 2,
. Наконец, согласно утверждению 2, 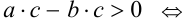
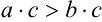 .
.
Достаточность. Пусть 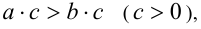 и требуется доказать, что а > b . Докажем методом «от противного». Так как а не может быть равно b , иначе по свойству 6 числовых равенств имели бы
и требуется доказать, что а > b . Докажем методом «от противного». Так как а не может быть равно b , иначе по свойству 6 числовых равенств имели бы 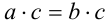 , то предположим, что а < b. Тогда, согласно доказанному выше свойству 1 числовых неравенств, это равносильно тому, что b > а . Согласно утверждению 2,
, то предположим, что а < b. Тогда, согласно доказанному выше свойству 1 числовых неравенств, это равносильно тому, что b > а . Согласно утверждению 2, 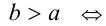
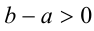 . Далее, поскольку b — а > 0 ,c>0, то, согласно утверждению 5,
. Далее, поскольку b — а > 0 ,c>0, то, согласно утверждению 5, 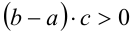 . Раскрывая скобки в соответствии с распределительным законом, получаем, что тогда
. Раскрывая скобки в соответствии с распределительным законом, получаем, что тогда 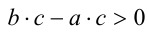 . Согласно утверждению 2, последнее неравенство равносильно
. Согласно утверждению 2, последнее неравенство равносильно 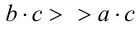 , что противоречит условию. Следовательно, а > b.
, что противоречит условию. Следовательно, а > b.
б) Докажем, что если c < 0 , то неравенство а > b равносильно неравенству 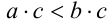 . Так как c < 0 , то, согласно утверждению 6,
. Так как c < 0 , то, согласно утверждению 6,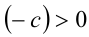 . Воспользуемся только что доказанным свойством 4.а:
. Воспользуемся только что доказанным свойством 4.а: 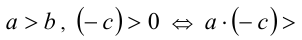
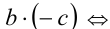 (по закону дистрибутивности)
(по закону дистрибутивности)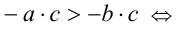 (по свойству 1 числовых неравенств)
(по свойству 1 числовых неравенств)  (по утверждению 3)
(по утверждению 3) 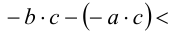
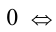 (согласно распределительному закону)
(согласно распределительному закону)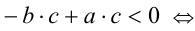 (по переместительному закону)
(по переместительному закону) 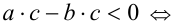 (по утверждению 3)
(по утверждению 3) 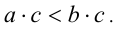
Пусть а > b, с > d . Докажем, что тогда а + с > b + d . Так как а > b и c > d, то (по утверждению 2) это равносильно тому, что а-b> 0, с — d > 0 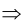 (по утверждению 4) (а — b) + (с — d) > 0
(по утверждению 4) (а — b) + (с — d) > 0 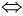 (согласно сочетательному и распределительному законам) (а + с) — (b + d)> 0
(согласно сочетательному и распределительному законам) (а + с) — (b + d)> 0 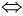 (по утверждению 2) а + с > b + d .
(по утверждению 2) а + с > b + d .
Рассмотрим краткое доказательство свойства (1) (более подробное доказательство этого, а также последующих свойств со всеми необходимыми обоснованиями и ссылками проведите самостоятельно).
Пусть 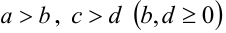 . Требуется доказать, что
. Требуется доказать, что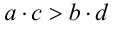 . Рассмотрим разность
. Рассмотрим разность 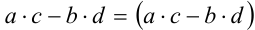
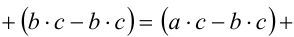
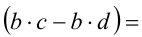
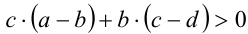 (так как в каждом из последних слагаемых оба сомножителя положительны), т.е.
(так как в каждом из последних слагаемых оба сомножителя положительны), т.е. 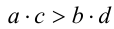
а) Необходимость докажем «от противного». Пусть b > 0, но 1/b < 0 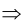 —1/b>0. Перемножим последнее неравенство с неравенством Ь> 0:
—1/b>0. Перемножим последнее неравенство с неравенством Ь> 0: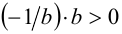 , т.е. — 1 > 0 . Из противоречия
, т.е. — 1 > 0 . Из противоречия 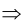 1/b > 0 .
1/b > 0 .
Достаточность. Пусть теперь 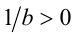 . Умножим это неравенство на верное неравенство
. Умножим это неравенство на верное неравенство 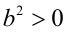 и получим
и получим 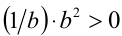 , т.е.
, т.е. 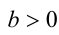 .
.
б) Пусть 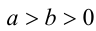 . Так как
. Так как 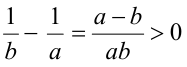 (числитель и знаменатель дроби положительны), то отсюда и вытекает доказываемое свойство.
(числитель и знаменатель дроби положительны), то отсюда и вытекает доказываемое свойство.
а) По свойству 6 умножим неравенство 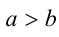 само на себя и получим
само на себя и получим 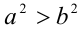 . Полученное неравенство ещё раз умножим на
. Полученное неравенство ещё раз умножим на 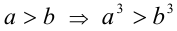
т.д. Таким образом, для любого конечного n за n шагов получим 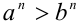 .
.
б) Воспользуемся формулой сокращённого умножения
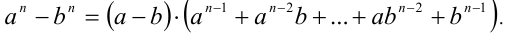
Так как выражение во вторых скобках положительно, то знак разности 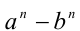 совпадает со знаком
совпадает со знаком 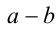 .
.
в) Докажите свойство самостоятельно.
Примеры задач, в которых используются указанные выше свойства числовых равенств и неравенств, можно встретить практически в любом разделе современной математики. Чаще всего подобные свойства используются при сравнении между собой чисел, в задачах на преобразования алгебраических и прочих выражений, на доказательство тождеств и неравенств, а также при получении разнообразных оценок для числовых выражений и значений функций.
Пример №118.
Пусть 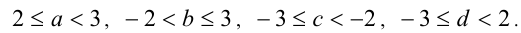
Оценить, какие значения могут принимать 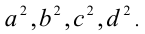
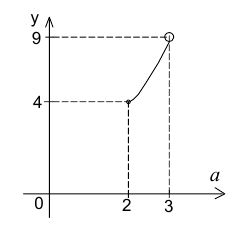
Решение. Пусть известно, что 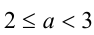 , оценим возможные значения величины
, оценим возможные значения величины 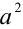 . Воспользуемся графическим подходом. Рассмотрим функцию
. Воспользуемся графическим подходом. Рассмотрим функцию 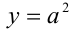 и найдём область её изменения на указанном выше полуинтервале.
и найдём область её изменения на указанном выше полуинтервале.
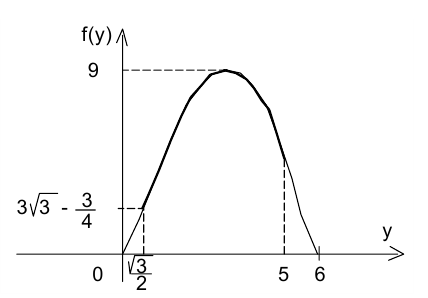
Как следует из графика, функция принимает все значения от 4 до 9 (не включая 9). Аналогично оцениваются 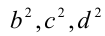 . Ответ:
. Ответ: 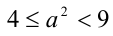 ,
,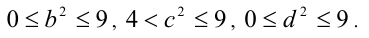
Пример №119.
Известно, что 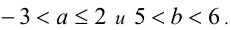 . Оценить значения:
. Оценить значения:
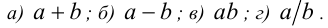
Решение:
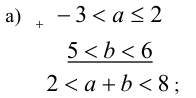
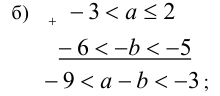
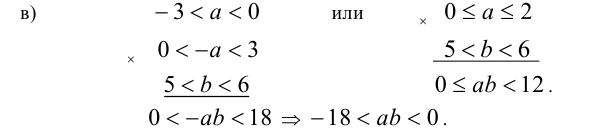
Объединяя полученные результаты, получим: 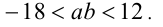
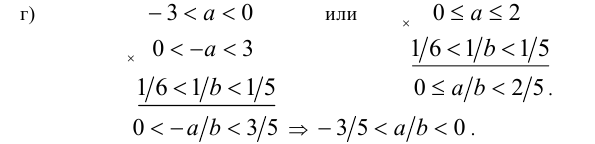
Объединяя полученные результаты, получим: 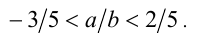
Ответ-. 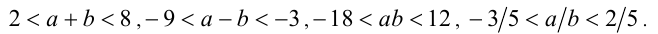
Пример №120.
Найти наибольшее и наименьшее значения выражения 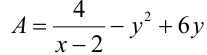 , если —
, если — 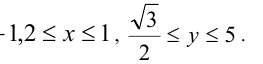
Решение:
Оценим вначале, какие значения может принимать дробь 4/(х — 2). Поскольку 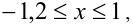 то
то 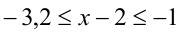 , а, значит,
, а, значит, 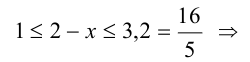
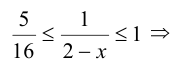
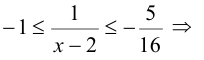
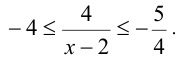
Теперь оценим выражение  Если представить график квадратичной функции
Если представить график квадратичной функции  на отрезке
на отрезке  , то имеем вершину параболы при
, то имеем вершину параболы при 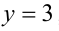 , при этом
, при этом 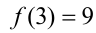 . Наименьшее значение функции на указанном отрезке достигается при
. Наименьшее значение функции на указанном отрезке достигается при 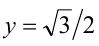 и равно
и равно 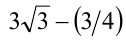 . Таким образом,
. Таким образом, 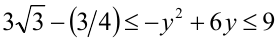 . Складывая полученные оценки для выражений
. Складывая полученные оценки для выражений 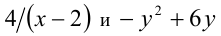 , приходим к ответу:
, приходим к ответу:
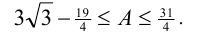
Пример №121.
Числа 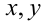 изменяются в пределах:
изменяются в пределах: 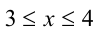
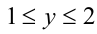 . В каких пределах изменяется выражение
. В каких пределах изменяется выражение
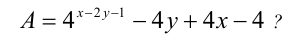
Решение:
Поскольку 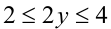 т.е.
т.е. 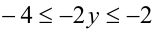 и
и 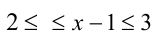 , то, складывая последние два неравенства, получаем оценку:
, то, складывая последние два неравенства, получаем оценку:
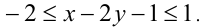
В силу монотонного возрастания показательной функции с основанием 4 имеем

Аналогично находим, что

Оба выражения 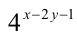 и
и 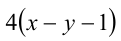 достигают своих наименьшего и наибольшего значений одновременно, при одних и тех же значениях x и у . Их наименьшие значения достигаются при
достигают своих наименьшего и наибольшего значений одновременно, при одних и тех же значениях x и у . Их наименьшие значения достигаются при 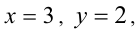 а наибольшие соответственно при
а наибольшие соответственно при 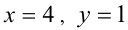 . Это вытекает из того, что оба выражения монотонно возрастают по x и независимо от этого монотонно убывают по у . Складывая почленно неравенства (1) и (2), получаем:
. Это вытекает из того, что оба выражения монотонно возрастают по x и независимо от этого монотонно убывают по у . Складывая почленно неравенства (1) и (2), получаем:
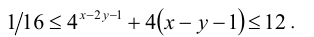
Ответ: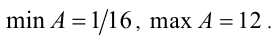
Пример №122.
Какие значения может принимать функция
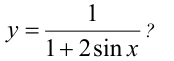
Решение:
Так как 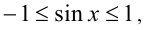 то
то 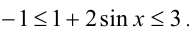 Обозначим
Обозначим 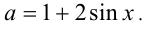 Таким образом, задачу можно сформулировать в виде: «Оценить, какие значения может принимать величина
Таким образом, задачу можно сформулировать в виде: «Оценить, какие значения может принимать величина 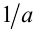 , если известно, что
, если известно, что 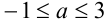 ». Поскольку
». Поскольку 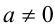 , рассмотрим отдельно два промежутка:
, рассмотрим отдельно два промежутка: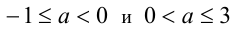 . В первом случае имеем:
. В первом случае имеем: 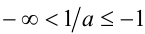 , а во втором:
, а во втором: 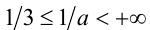 . Объединяя, получаем ответ.
. Объединяя, получаем ответ.
Ответ: 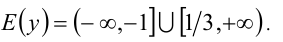
Пример №123.
Доказать неравенство,
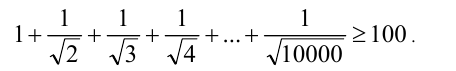
Доказательство. Очевидно, что при любом 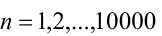 справедливы неравенства
справедливы неравенства 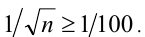
Складывая эти неравенства, получим:
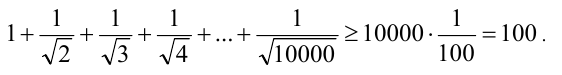
Неравенство также может быть доказано методом математической индукции.
Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:
Эти страницы возможно вам будут полезны:

