Оглавление:
Решение уравнений в рациональных числах
Когда по условию задачи необходимо найти рациональные корни уравнения, возможны следующие подходы.
Во-первых, можно сначала полностью решить уравнение, найти все его корни, и лишь затем отобрать среди них рациональные. Однако следует помнить, что этот подход в некоторых случаях бывает нецелесообразен.
Во-вторых, можно целенаправленно искать только рациональные корни. Один из таких способов поиска рациональных корней у алгебраических многочленов с целыми (рациональными) коэффициентами будет рассмотрен ниже в пункте 3.3.1 раздела 3. Сейчас обратимся к примерам, в которых при решении задач, связанных с рациональными корнями уравнений, используются определение и свойства рациональных чисел.
Пример №82.
При каких целочисленных значениях параметра а корни уравнения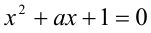 являются рациональными числами?
являются рациональными числами?
Решение:
При условии 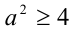 найдём корни этого квадратного уравнения:
найдём корни этого квадратного уравнения: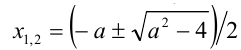 . Так как по условию
. Так как по условию 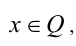 то
то 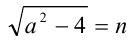
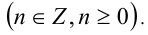 Возведём последнее равенство в квадрат:
Возведём последнее равенство в квадрат:
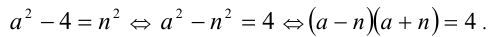
Так как 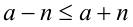 , то возможны лишь следующие случаи:
, то возможны лишь следующие случаи:
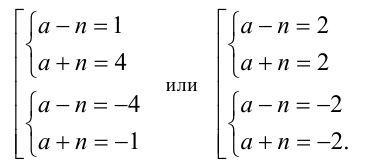
Решая эти системы в целых числах, находим ответ: 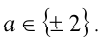
Пример №83.
Доказать, что уравнение 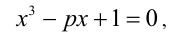 , где
, где 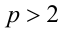 целое, не имеет рациональных корней.
целое, не имеет рациональных корней.
Доказательство (от противного). Предположим, что уравнение имеет рациональный корень 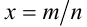 , где
, где 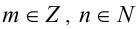 . Тогда подставим его в уравнение:
. Тогда подставим его в уравнение:
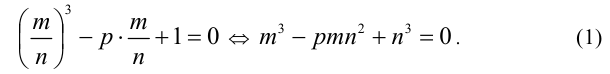
1) Перепишем уравнение (1) в виде
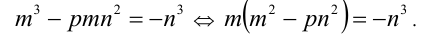
Проведём анализ делимости. Целочисленное выражение в левой части равенства кратно m , а значит, и выражение в правой части должно делиться на m нацело: 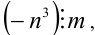 но отсюда следует, что
но отсюда следует, что 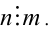
2) Теперь перепишем уравнение (I) в виде
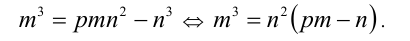
Аналогичными рассуждениями получим, что так как выражение в правой части равенства кратно 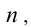 то и выражение
то и выражение 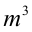 в левой его части делится на n нацело, а, следовательно,
в левой его части делится на n нацело, а, следовательно, 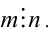
Из того, что одновременно 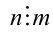 и
и 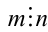 , заключаем, что это возможно, только если
, заключаем, что это возможно, только если 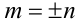 . Иными словами, мы показали, что если у рассматриваемого уравнения есть рациональные корни, то это могут быть только числа
. Иными словами, мы показали, что если у рассматриваемого уравнения есть рациональные корни, то это могут быть только числа 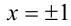 . Осталось сделать проверку.
. Осталось сделать проверку.
Подставляя значение x = 1 в уравнение, получим р = 2 , что противоречит условию задачи. При : x = — 1 находим р = 0 , что также противоречит условию задачи. Следовательно, рациональных корней у уравнения нет.
Пример №84.
Найти все такие рациональные числа x и у, которые удовлетворяют уравнению
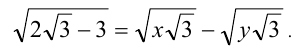
Решение:
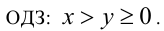 Так как на
Так как на 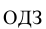 обе части данного иррационального уравнения неотрицательны, то возведём уравнение в квадрат и получим равносильное уравнение
обе части данного иррационального уравнения неотрицательны, то возведём уравнение в квадрат и получим равносильное уравнение
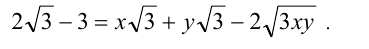
Сократим на 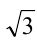 и уединим единственным радикал в левой части уравнения
и уединим единственным радикал в левой части уравнения
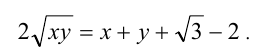
Записав условие неотрицательности правой части 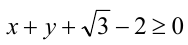 для сохранения равносильности преобразования, ещё раз возведём уравнение в квадрат (используя формулу квадрата суммы 4-х чисел):
для сохранения равносильности преобразования, ещё раз возведём уравнение в квадрат (используя формулу квадрата суммы 4-х чисел):
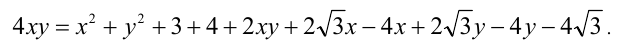
Приведём полученное уравнение к виду
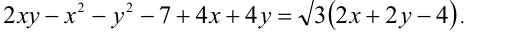
Заметим, что в левой части находится рациональное выражение. Выражение в скобках в правой части равенства также рационально. Известно, что произведение рационального числа 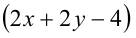 на иррациональное
на иррациональное 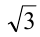 может быть рациональным тогда и только тогда, когда
может быть рациональным тогда и только тогда, когда 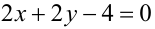 , при этом выражение
, при этом выражение 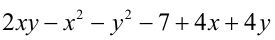 также должно обращаться в нуль. Таким образом, условия задачи выполняются, только если система
также должно обращаться в нуль. Таким образом, условия задачи выполняются, только если система
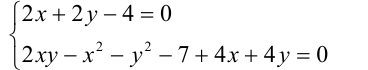
имеет решения. Решив систему, находим две пары 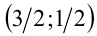 и
и 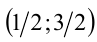 . Проверка показывает, что только первая пара удовлетворяет
. Проверка показывает, что только первая пара удовлетворяет 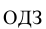 и условию
и условию 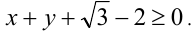
Ответ: 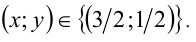
Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:
Эти страницы возможно вам будут полезны:

