Оглавление:
Сравнение рациональных чисел. Арифметические операции над рациональными числами
Два рациональных числа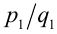 
и 
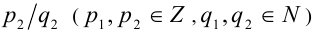считаются, по определению, равными, если 
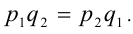Число 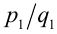считается большим числа 
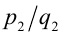если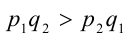 
и меньшим этого числа, если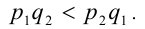 
Пусть q — натуральное число. Если р — натуральное число, то число р /q называется положительным рациональным числом, или положительной дробью. Если же р — целое отрицательное число, то число p/q называется отрицательным рациональным числом, или отрицательной дробью. Если р равно нулю, то число p/q называется нулевой дробью.
Определим основные арифметические операции на множестве рациональных чисел. Пусть даны два рациональных числа .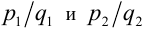
. Суммой двух этих чисел назовем рациональное число, равное 
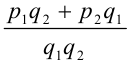. Произведением двух рациональных чисел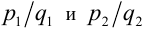, назовём рациональное число, равное 
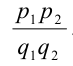. Разность и частное двух рациональных чисел определяются аналогично тому, как они вводились для натуральных и целых чисел (т.е. через определения суммы и произведения), при этом их значения всегда можно находить по формулам:
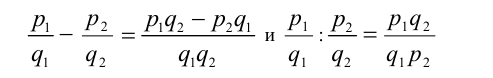
(в последнем случае предполагается, что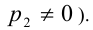 
Сумма, разность, произведение и частное двух (конечного числа) рациональных чисел всегда существуют и являются рациональными числами. Это означает, что множество рациональных чисел замкнуто относительно четырёх арифметических операций. При этом рассмотренные арифметические операции над рациональными числами удовлетворяют тем же законам коммутативности, ассоциативности и дистрибутивности, что и для натуральных и целых чисел.
Пример №75.
Сравнить два числа
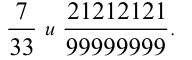
Решение:
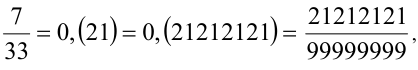т.е. числа равны.
Пример №76.
Что больше.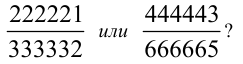 
Решение:
Обозначим число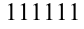 
через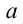 
. Тогда первая дробь равна 
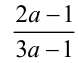, а вторая 
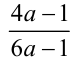. Для ответа на поставленный вопрос составим разность этих дробей и определим её знак:
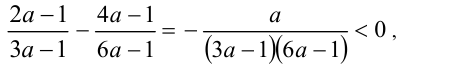
значит, вторая дробь больше.
Пример №77.
Что больше: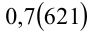 
или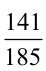 
?
Решение:
Числа удобнее сравнивать, когда они записаны в одном представлении. Поэтому, например, переведём периодическую десятичную дробь к виду обыкновенной дроби:
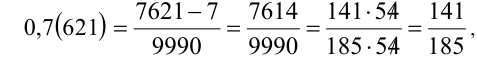
т.е. числа равны.
Пример №78.
Сравнить числа: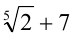 
и 
.
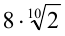Решение:
Обозначим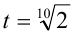 
. Тогда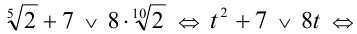 
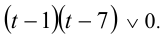
Заметим, что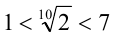 
и поэтому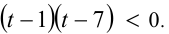 
Ответ: первое число меньше.
Пример №79.
Сравнить два числа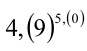 
и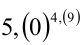 
.
Решение:
Воспользуемся изложенным выше правилом перевода периодической дроби в обыкновенную:
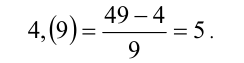
С другой стороны, очевидно, 5,(0) = 5 . Таким образом, числа оказались равны (!).
Замечание. Одно и то же целое число 5 можно представить двумя способами в виде периодической дроби: 4,(9) и 5,(О), и эти представления эквивалентны.
Ответ: числа равны.
Пример №80.
Числа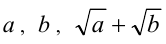 
— рациональные. Доказать, что 
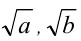,также рациональные числа.
Доказательство. Воспользуемся тем, что сумма, разность, произведение и частное двух рациональных чисел есть рациональное число. Поскольку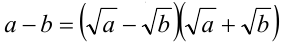 
а числа 
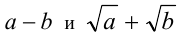рациональны (первое как разность двух рациональных чисел, второе по условию), то число 
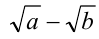также рационально. Тогда 
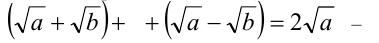рационально, следовательно,
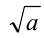будет рационально; аналогично,
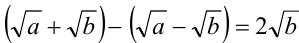рационально, а значит, 
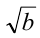также рационально, что и требовалось доказать.
Пример №81.
Найти все рациональные числа x , при которых выражение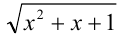 
является рациональным числом.
Решение:
Рассмотрим решение этой задачи, основанное на методе «от частного к общему» (см. пункт 3.4 раздела 3).
Заметим, что если условия задачи выполняются, то, в частности, число
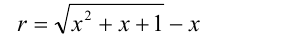
является рациональным. Выражая x из последнего равенства, как следствие получим, что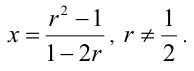 
Рассмотрим теперь множество всех чисел x вида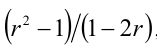 
, где r — любое рациональное число, не равное 1/2 . Покажем, что все такие числа удовлетворяют условиям задачи. В самом деле,
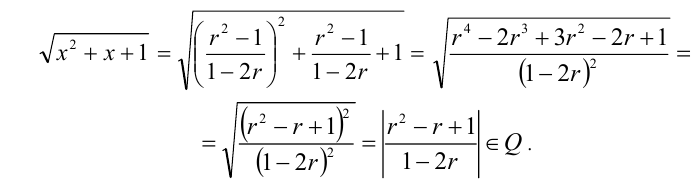
Ответ: это числа вида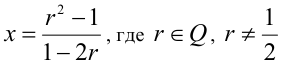 
-любое.
Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:
Эти страницы возможно вам будут полезны:
