Оглавление:
Уравнения вида A*B=n, где А, В — целочисленные выражения, п — целое число
Пусть решаемое в целых числах уравнение удалось преобразованиями привести к виду, когда в одной из его частей оказывается произведение двух (нескольких) целочисленных множителей А, В , а в другой, соответственно, целое число n . В такой ситуации решение уравнения сводится к перебору всех возможных случаев, когда n представимо в виде такого произведения целых чисел (количество вариантов будет конечно и тем меньше, чем меньше целых делителей имеет число п , стоящее в правой части уравнения).
Пример №67.
Для всех значений параметра 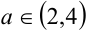 найти все целые числа x и y, удовлетворяющие равенству
найти все целые числа x и y, удовлетворяющие равенству 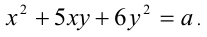
Решение:
Так как слева от знака равенства находится целое число, то а должно быть целым, следовательно, а = 3 . Итак, имеем:
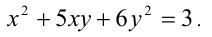
Разложим левую часть уравнения на множители:
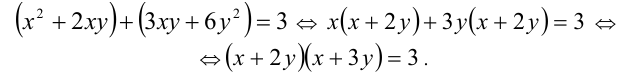
Так как при целых x ,у оба сомножителя в левой части целочисленны, то число 3 в правой части можно разложить на произведение двух целых чисел следующими способами:
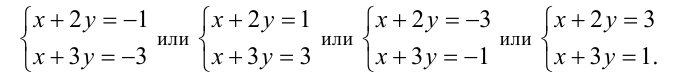
Ответ: при а = 3 — четыре решения
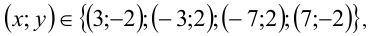
при 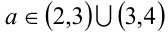 уравнение не имеет решений.
уравнение не имеет решений.
Пример №68.
Найти все пары целых чисел x и у, удовлетворяющих уравнению 3ху + 16х + 13у + 61 = 0.
Решение:
Умножим уравнение на 3 и после этого, группируя и вынося общий множитель за скобку, приведём к необходимому виду:
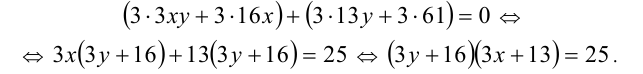
Число 25 можно представить в виде произведения двух целочисленных сомножителей следующими способами:
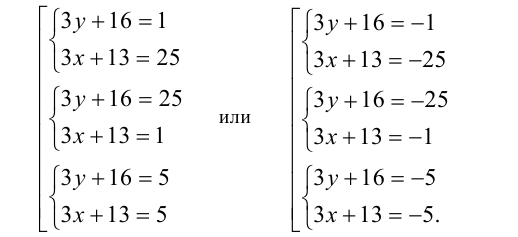
Только три из перечисленных шести систем имеют решения в целых числах.
Ответ: 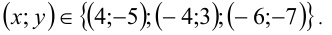
Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:
Эти страницы возможно вам будут полезны:

