Оглавление:
Задачи на НОД и НОК
Следующие примеры демонстрируют приёмы, используемые при решении задач из данной группы.
Пример №42.
Найти, пользуясь стандартным алгоритмом, НОД и НОК чисел 42,18.
Решение:
1) Найдём вначале НОД(42,18). Для этого выпишем разложения чисел 42 и 18 на простые множители: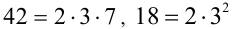 . Наконец, выбирая наименьшие степени, с которыми простые множители 2, 3 и 7 входят в разложение каждого из двух чисел, находим
. Наконец, выбирая наименьшие степени, с которыми простые множители 2, 3 и 7 входят в разложение каждого из двух чисел, находим
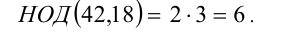
2) Найдём теперь НОК( 42,18). В отличие от предыдущего случая, теперь выбираем наибольшие степени для каждого из простых чисел:
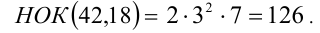
Пример №43.
Используя различные свойства, найти НОД и НОК чисел 42,18.
Решение:
1) Решим задачу с помощью свойства 6:
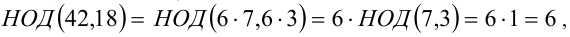
так как числа 7 и 3 взаимно просты;
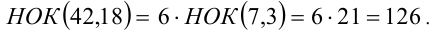
2) Теперь найдём НОД(42,18) другим способом, применяя несколько раз свойство 9:
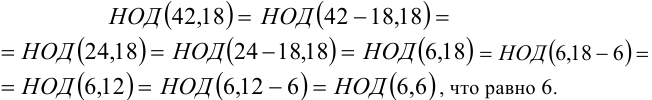
Пример №44.
Найти, пользуясь алгоритмом Евклида,
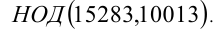
Решение:
Применяя алгоритм Евклида, получаем
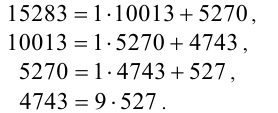
Следовательно, 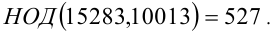 Итак, сначала делят большее число на меньшее, меньшее число на остаток от деления и так далее, пока остаток не станет равен нулю. Последний ненулевой остаток и является наибольшим общим делителем исходных чисел.
Итак, сначала делят большее число на меньшее, меньшее число на остаток от деления и так далее, пока остаток не станет равен нулю. Последний ненулевой остаток и является наибольшим общим делителем исходных чисел.
Пример №45.
Найти наибольший общий делитель чисел 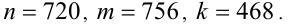
Решение:
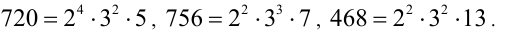
Поэтому 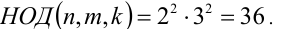
Пример №46.
Найти такие натуральные числа а и b, что НОД(а,b)= 3, НОК(а,b)= 630, и при этом сумма а + b минимальна.
Решение:
Так как НОД(аb)= 3, то по свойству 3 существуют такие взаимно простые натуральные числа m,n , что а = Зm, b = Зn. Тогда задачу можно сформулировать в виде: «Найти такие натуральные m,n что НОД(m,n) = 1, НОК(m,n) = 210 , и при этом сумма m + n минимальна».
Далее задача решается перебором. Заметим, что условия симметричны относительно m и n. Пусть, ради определённости, 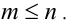 Так как
Так как 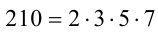 ,то возможны следующие случаи:
,то возможны следующие случаи:
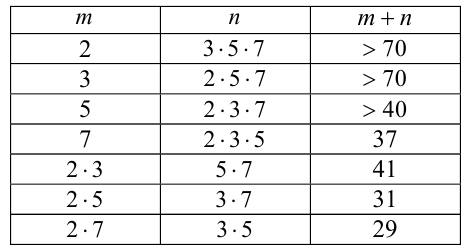
Итак, сумма m+n минимальна (и равна 29), если m= 14, n = 15. Им соответствуют а= 42 , b = 45 . С учётом симметрии получаем ответ. Ответ: 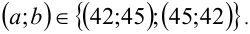
Пример №47.
Натуральные числа а,b и c таковы, что НОК(а,b)= 60 и НОК(а,с) = 270. Найти НОК(b,с).
Решение:
Сравним разложения на простые множители чисел
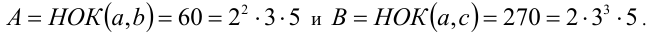
Исходя из вида А , предположим, что а делится на 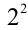 , тогда
, тогда 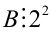 . Но это не так, следовательно, на
. Но это не так, следовательно, на 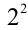 делится число b . Аналогично, предположим, что а делится на
делится число b . Аналогично, предположим, что а делится на 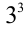 , тогда
, тогда 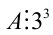 . Поскольку это не так, то на
. Поскольку это не так, то на 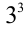 делится число С .
делится число С .
Поэтому число С = НОК(b,с) делится на произведение 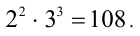
Множитель 5 может либо присутствовать в разложении хотя бы одного из чисел b и c, либо нет. Соответственно, получаем 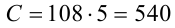 . Отметим, что первый случай реализуется, например, для чисел а = 1, b = 60 , с = 270, а второй — для
. Отметим, что первый случай реализуется, например, для чисел а = 1, b = 60 , с = 270, а второй — для 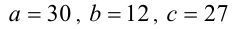
Ответ: 108 или 540.
Пример №48.
Натуральные числа n и m таковы, что НОД(n,m)+НОК(n,m)=n+m . Доказать, что одно из них является делителем другого.
Решение:
Обозначим d = НОД(n,m), тогда по свойству 3 существуют такие натуральные p,q , НОД(р,q)= 1, что п = pd, m= qd .
Подставим в исходное равенство:
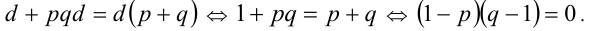
Если 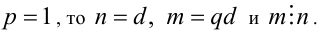
Если 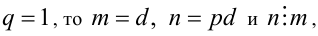 что и требовалось доказать.
что и требовалось доказать.
Пример №49.
Интервалы движения городских автобусов по трём маршрутам, проходящим через общую остановку, составляют 15, 20 и 24 минуты соответственно. Сколько раз с 7-55 до 17-05 того же дня на этой остановке одновременно встречаются автобусы всех трёх маршрутов, если одна из таких встреч происходит в 12-35?
Решение:
Предположим, в некоторый момент времени все три автобуса встретились на остановке. Найдём, через сколько минут они вновь повстречаются на этой остановке. Так как 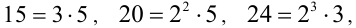 то НОК(15,20,24) = 120. Отсчитывая этот отрезок времени от 12-35, находим все моменты встреч, попадающие в заданный промежуток: 8-35, 10-35, 12-35, 14-35, 16-35. Всего 5 раз.
то НОК(15,20,24) = 120. Отсчитывая этот отрезок времени от 12-35, находим все моменты встреч, попадающие в заданный промежуток: 8-35, 10-35, 12-35, 14-35, 16-35. Всего 5 раз.
Пример №50.
Найти числа x,у, если известно, что они натуральные и таковы, что 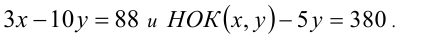
Решение:
Пусть d = НОД(x,у), тогда по свойству 3 получаем, что найдутся такие натуральные числа n , k , что 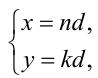 причём НОД(n,k)=1.
причём НОД(n,k)=1.
Тогда НОК(х,у)= nkd , и условия задачи можно представить в виде следующей системы:
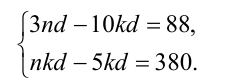
Из первого уравнения системы следует, что 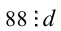 , т.е.
, т.е. 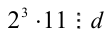 , а из второго — что
, а из второго — что 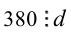 , т.е.
, т.е. 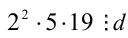 . Очевидно, что числа 88 и 380 имеют общими натуральными делителями только 1,2 и 4. Следовательно, d может принимать одно из этих значений:
. Очевидно, что числа 88 и 380 имеют общими натуральными делителями только 1,2 и 4. Следовательно, d может принимать одно из этих значений: 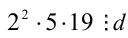 . Рассмотрим эти случаи в отдельности.
. Рассмотрим эти случаи в отдельности.
1) Если d = 1, то система примет вид 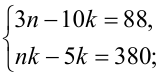 решая систему в натуральных числах, получаем, что она не имеет решений.
решая систему в натуральных числах, получаем, что она не имеет решений.
2) Если d = 2 , то система примет вид 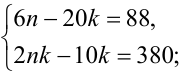 решая её в натуральных числах, также получаем, что нет решений.
решая её в натуральных числах, также получаем, что нет решений.
3) Если d = 4, то имеем систему 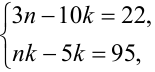 откуда находим
откуда находим 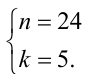 Тогда окончательно получаем
Тогда окончательно получаем 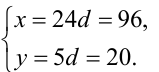
Ответ: 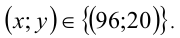
Следующую группу методов можно отнести к универсальным, т.е. используемым при решении произвольных задач (не только с целочисленными величинами).
Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:
Эти страницы возможно вам будут полезны:
| Метод анализа последней цифры числа в математике |
| Задачи на простые и составные числа в математике |
| Метод замены переменных в математике |
| Метод оценок в математике с примерами решения |

