Оглавление:
Задачи на простые и составные числа
Если необходимо выяснить, является ли заданное число простым, то используемый при этом подход основан на попытке разложения исследуемого числа на простые множители, нахождение его делителей, отличных по модулю от единицы и самого числа.
Пример №34.
Доказать, что число р = 389 — простое.
Доказательство. Для доказательства нет необходимости, перебирая все простые числа от 2 до ближайшего к числу р , проверять, делится ли на каждое из них данное число (если ни на одно из них не делится — значит, простое). Достаточно убедиться в том, что р не делится нацело ни на одно простое число от 2 до 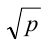 (попробуйте объяснить, почему). В данном примере достаточно проверить, что число р = 389 не делится на
(попробуйте объяснить, почему). В данном примере достаточно проверить, что число р = 389 не делится на
2, 3, 5, 7, 11, 13, 17, 19.
Пример №35.
Является ли простым число
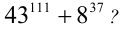
Решение:
Заметим, что данное число есть сумма кубов двух чисел, и разложим его на множители по соответствующей формуле:
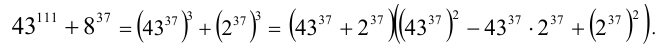
Поскольку число удалось разложить на произведение двух натуральных сомножителей, каждый из которых, очевидно, отличен от единицы, то это означает, по определению составного числа, что исходное число было составным.
Пример №36.
Установить, является ли число 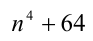 простым или составным.
простым или составным.
Решение:
Очевидно, достаточно ограничиться рассмотрением случая натуральных n (при целых отрицательных п результат будет аналогичен, а при n = 0 число будет составным). Чтобы дать ответ на этот вопрос, попробуем разложить данное число на множители:
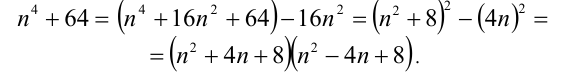
Заметим, что  каждый из двух сомножителей строго больше единицы (докажите это). Это означает, что исходное число — составное.
каждый из двух сомножителей строго больше единицы (докажите это). Это означает, что исходное число — составное.
Пример №37.
Установить, является простым или составным число
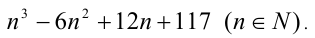
Решение:
Преобразуем данное выражение, выделив в нём полный куб разности
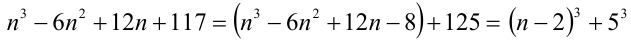
Теперь разложим на множители по формуле суммы кубов:
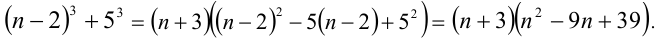
Очевидно, что при натуральных n оба сомножителя в этом произведении цело-численны и больше единицы. Это означает, что исследуемое число является составным.
Пример №38.
Доказать, что квадрат любого простого числа р > 3 при делении на 12 даёт в остатке 1.
Доказательство. Воспользуемся известным свойством, что любое простое число, большее 3, можно представить в виде 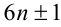 . Тогда его квадрат равен
. Тогда его квадрат равен 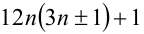 , откуда и вытекает требуемое утверждение.
, откуда и вытекает требуемое утверждение.
Пример №39.
Пусть р > 5 — простое число. Доказать, что 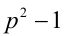 делится нацело на 24.
делится нацело на 24.
Доказательство.
Рассмотрим на числовой прямой три последовательных целых числа 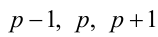 . Так как р — простое число, то р нечётно
. Так как р — простое число, то р нечётно 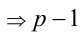 и
и 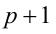 — чётные последовательные числа, следовательно, одно из них делится на 2, а другое — на 4, но тогда их произведение
— чётные последовательные числа, следовательно, одно из них делится на 2, а другое — на 4, но тогда их произведение 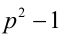 делится на 8. Далее, поскольку
делится на 8. Далее, поскольку 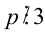 , то либо
, то либо 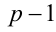 , либо
, либо 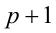 делится на 3, а значит, их произведение кратно 3. Итак, число
делится на 3, а значит, их произведение кратно 3. Итак, число 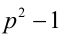 делится одновременно на 8 и на 3
делится одновременно на 8 и на 3 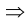 делится на 24.
делится на 24.
Пример №40.
Найти все простые числа вида
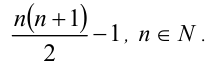
Решение:
Обозначим 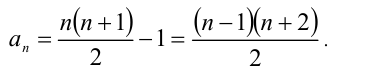
1) Если 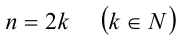 , то
, то 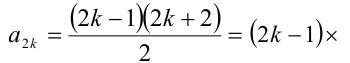
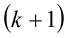 . При натуральных k оба сомножителя натуральны, причём второй сомножитель больше 1, поэтому
. При натуральных k оба сомножителя натуральны, причём второй сомножитель больше 1, поэтому 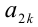 может быть простым числом, только если
может быть простым числом, только если 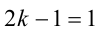 т.е. при
т.е. при 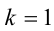 , тогда
, тогда 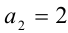 .
.
2) Если 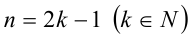 , то имеем
, то имеем
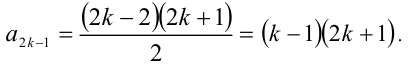
При k = 1 имеем 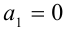
, =0 — не является ни простым, ни составным числом. При k > 2 оба сомножителя целочислснны и больше 1 и, значит, число будет составным. Только при k = 2 получаем простое число 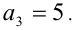
Ответ: таких чисел два: 2 и 5.
Пример №41.
Доказать, что для всех простых чисел 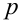 число
число 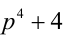 — составное.
— составное.
Решение:
1-й способ. Разложим исследуемое число на множители:
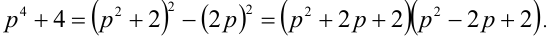
Так как при простых 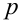 оба сомножителя больше единицы (убедитесь в этом самостоятельно), то тем самым необходимое утверждение доказано.
оба сомножителя больше единицы (убедитесь в этом самостоятельно), то тем самым необходимое утверждение доказано.
2-й способ. Покажем, что если 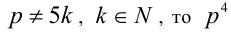 при делении на 5 даёт остаток 1:
при делении на 5 даёт остаток 1:
1) 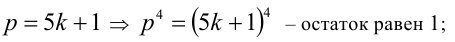
2) 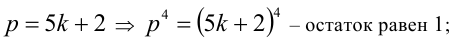
3) 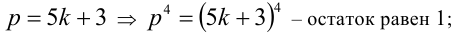
4) 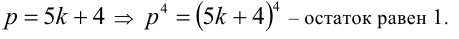
Тогда число 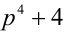 делится нацело на 5, а значит, является составным. Если же
делится нацело на 5, а значит, является составным. Если же 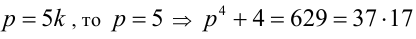 — составное.
— составное.
Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:
Эти страницы возможно вам будут полезны:
| Метод анализа остатков в математике |
| Метод анализа последней цифры числа в математике |
| Задачи на НОД и НОК в математике |
| Метод замены переменных в математике |

