Оглавление:
Метод анализа последней цифры числа
В ряде случаев удобным оказывается так называемый метод анализа последней (последних) цифры числа.
Пример №30.
Доказать, что число 19981999200020012002 не является квадратом целого числа.
Доказательство. Натуральное число п может оканчиваться на любую из десяти цифр: 0, 1,2, 3, 4, 5, 6, 7, 8, 9. Выясним, на какую цифру при этом может оканчиваться квадрат этого числа:

Среди цифр, на которые оканчивается 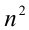 , отсутствует цифра «2». Поэтому данное число не может являться квадратом целого числа.
, отсутствует цифра «2». Поэтому данное число не может являться квадратом целого числа.
Пример №31.
Доказать, что ни при каком натуральном п число 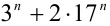 не является квадратом натурального числа.
не является квадратом натурального числа.
Решение:
Выясним, на какую цифру может оканчиваться число 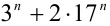 . Сделаем это последовательно. Сначала оценим последнюю цифру числа
. Сделаем это последовательно. Сначала оценим последнюю цифру числа 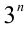

далее эта последовательность последних цифр 3,9,7,1,3,9,7,1,… циклически повторяется. Оценим теперь последние цифры чисел 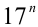 и
и 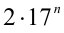 :
:
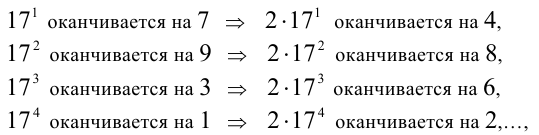
далее последовательность последних цифр 4,8,6,2,… также циклически повторяется. Суммируя, получаем,что

и далее эта последовательность последних цифр выражения 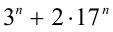 опять-таки циклически (с периодом 4) повторяется.
опять-таки циклически (с периодом 4) повторяется.
Таким образом, методом анализа последней цифры удалось установить, что при любых натуральных п число 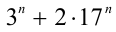 может оканчиваться только на цифры 3 или 7. Но квадрат никакого натурального числа этими цифрами не оканчивается (квадрат натурального числа может оканчиваться только на одну из цифр 0, 1,4, 5, 6, 9), что и доказывает утверждение.
может оканчиваться только на цифры 3 или 7. Но квадрат никакого натурального числа этими цифрами не оканчивается (квадрат натурального числа может оканчиваться только на одну из цифр 0, 1,4, 5, 6, 9), что и доказывает утверждение.
Пример №32.
Найти последнюю цифру числа 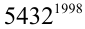 .
.
Решение:
Решим сначала более простую задачу, а именно найдём последнюю цифру числа 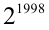 . Выясним, на какие цифры может оканчиваться натуральная степень числа 2:
. Выясним, на какие цифры может оканчиваться натуральная степень числа 2:
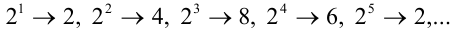
Очевидно, что при дальнейшем увеличении показателя степени последовательность последних цифр 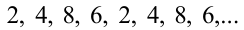 будет циклически повторяться. Представим число
будет циклически повторяться. Представим число 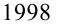 в виде:
в виде: 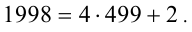 Имеем:
Имеем: 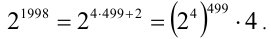 Заметим, что число
Заметим, что число 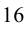 в скобках оканчивается цифрой
в скобках оканчивается цифрой 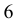 , и поэтому любая его натуральная степень также будет оканчиваться этой цифрой. Итак, число
, и поэтому любая его натуральная степень также будет оканчиваться этой цифрой. Итак, число 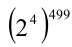 оканчивается цифрой
оканчивается цифрой 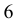 , и это число умножается на четыре. Поэтому последней цифрой их произведения будет
, и это число умножается на четыре. Поэтому последней цифрой их произведения будет 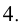 Если теперь повторить проведенные рассуждения для числа
Если теперь повторить проведенные рассуждения для числа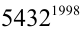 , то окажется (сделайте это самостоятельно), что добавление одной или нескольких цифр перед
, то окажется (сделайте это самостоятельно), что добавление одной или нескольких цифр перед 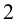 не оказывает влияния на полученный результат.
не оказывает влияния на полученный результат.
Ответ: число оканчивается цифрой 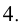
Пример №33.
Существует ли такое натуральное число n ,что 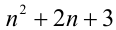 делится нацело на 2005?
делится нацело на 2005?
Решение:
Последней цифрой у натурального числа n может быть любая из цифр 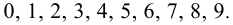 Последней цифрой у числа
Последней цифрой у числа 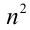 может быть соответственно
может быть соответственно 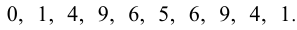 Тогда последняя цифра у числа
Тогда последняя цифра у числа 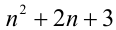 , как несложно посчитать, может соответственно принимать значения
, как несложно посчитать, может соответственно принимать значения 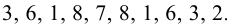 Но тогда это число не делится даже на
Но тогда это число не делится даже на 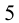 , а значит, не может делиться и на
, а значит, не может делиться и на 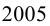 .
.
Существуют задачи, решение которых опирается на знание определений и свойств специфических групп целых чисел или же на определённые понятия. К таким задачам можно отнести задачи на простые числа, а также на НОК и НОД. Для их решения разработаны, в том числе, специальные приёмы, учитывающие их специфику. Рассмотрим примеры задач этого типа.
Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:
Эти страницы возможно вам будут полезны:
| Метод анализа делимости нацело. Использование признаков делимости |
| Метод анализа остатков в математике |
| Задачи на простые и составные числа в математике |
| Задачи на НОД и НОК в математике |

