Оглавление:
Метод анализа делимости нацело. Использование признаков делимости
Рассмотрим примеры, когда при решении задачи возникает необходимость проанализировать делимость нацело того или иного целочисленного выражения.
Пример №7.
Доказать, что при любом натуральном п выражение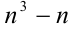 
делится нацело на 6.
Решение:
Преобразуем выражение к виду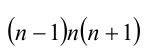 
и докажем, что произведение трёх последовательных целых чисел всегда делится нацело на 6. В самом деле, каждое второе целое число кратно двум, а каждое третье — трём. Поэтому можно утверждать, что среди подряд идущих чисел п — 1, п и п + 1 по крайней мере одно делится на 2, и (одновременно с этим) одно делится на 3. Следовательно, их произведение будет делиться на 6, что и требовалось доказать.
Замечание. Аналогичными рассуждениями можно доказать, что произведение четырёх последовательных натуральных чисел делится нацело на 24.
Пример №8.
Доказать, что число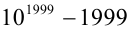 
делится нацело на 9.
Решение:
Преобразуем число к виду
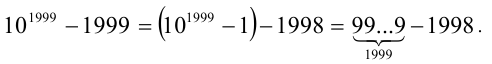
Каждое из двух слагаемых делится нацело на 9 по признаку делимости на 9. Следовательно, их разность также кратна 9, что и требовалось доказать.
Пример №9.
Найти все числа вида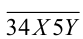 
такие, чтобы они делились без остатка на 36.
Решение:
Поскольку 36 = 4 • 9 , то воспользуемся признаками делимости на 4 и 9. Начнём с признака делимости на 4 (он использует только одну из двух неизвестных цифр). Число 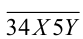кратно 4 тогда и только тогда, когда двузначное число 
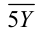делится нацело на 4, а это выполняется, только если Y = 2 или Y = 6 . Рассмотрим эти два случая и в каждом из них применим признак делимости на 9.
1) Если Y = 2, то число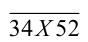 
должно делиться нацело на 9, т.е. сумма всех цифр данного числа 3 + 4 + Х + 5 + 2 = 14+Х должна быть кратна 9. Это возможно лишь при X = 4 . Имеем число 34452.
2) Если Y = 6, то число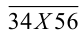 
кратно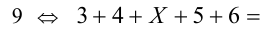 
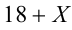кратно 9, т.е. X = 0 или X = 9. Таким образом, нашли ещё два числа: 34056 и 34956. Ответ: 34452, 34056 и 34956.
Пример №10.
Решить уравнение в целых числах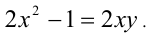 
Решение:
Заметим, что при целых X и Y в левой части уравнения стоит нечётное число, а в правой — чётное, что невозможно. Следовательно, данное уравнение не имеет решений в целых числах.
Пример №11.
Доказать, что уравнение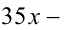 
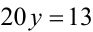не имеет целочисленных решении.
Доказательство. Достаточно заметить, что при целых X и Y выражение в левой части уравнения делится нацело на 5, а число 13 справа — нет. Полученное противоречие доказывает утверждение.
Пример №12.
Существуют ли целые числа т и п , удовлетворяющие уравнению
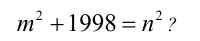
Решение:
Преобразуем уравнение к виду
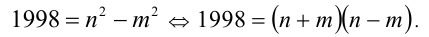
Так как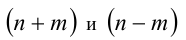 
— всегда числа одинаковой чётности, то их произведение 
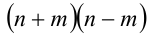либо нечётно (что невозможно, так как 1998 — чётное число), либо кратно четырём. Но 1998 на 4 не делится.
Ответ: не существуют.
Пример №13.
Решить в целых числах систему уравнений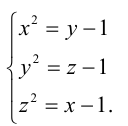 
Решение:
1-й способ. Из первого уравнения системы следует, что числа x и у имеют разную чётность (если одно четно, то другое — нечётно, и наоборот). Из второго уравнения аналогично следует, что у и z — разной чётности, а из третьего, что X и Z также имеют разную чётность, что невозможно.
2-й способ. Сложив все три уравнения системы, получим следствие
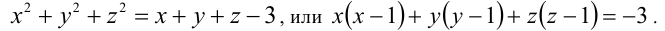
Левая часть последнего равенства чётна как сумма трёх чётных чисел (поскольку произведение любых двух последовательных целых чисел всегда чётно), а правая часть — нечётна, что невозможно. Ответ: нет решений в целых числах.
Пример №14.
Известно, что 4п = 5т . Найти все натуральные числа т и n , удовлетворяющие этому равенству.
Решение:
Целочисленное выражение 4n в левой части равенства кратно 4, следовательно, и выражение 5т справа также должно делиться на 4 нацело. Но так как 5 на 4 нацело не делится, то, значит,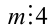
, т.е. для любого т , удовлетворяющего исходному равенству, найдётся такое число 
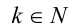, что 
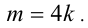Подставим в равенство: 
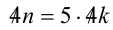, откуда 
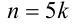. Итак, уравнение имеет бесконечно много решений в натуральных числах, общий вид которых
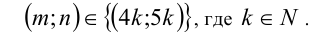
Пример №15.
При каких наименьших натуральных значениях n и m выполняется равенство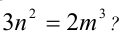 
Решение:
1) Заметим, что левая часть уравнения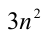 
делится нацело на 3, следовательно, и правая часть уравнения 
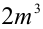должна делиться на 3, а значит, m должно быть кратно 3, т.е.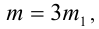 
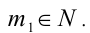Аналогично правая часть уравнения 
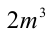кратна 2, следовательно, и левая часть 
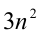должна делиться на 2, а значит, n должно быть кратно 2, т.е. 
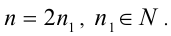Подставим в уравнение:
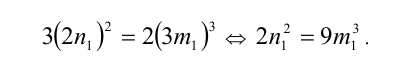
2) Так как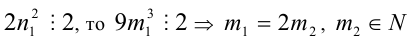 
; аналогично рассуждая, получим, что, так как 
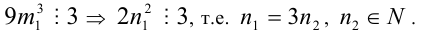Подставим в последнее уравнение:
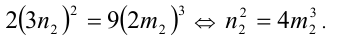
3) Так как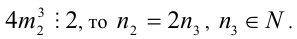 
Подставим в уравнение:
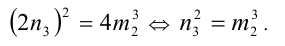
Очевидно, что последнее равенство выполняется при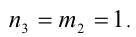 
Это наименьшие возможные натуральные значения 
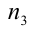и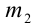 
, и им соответствуют наименьшие возможные значения п и т . Найдём их.
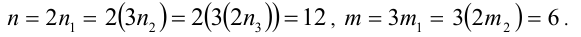
Ответ: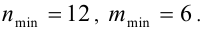 
Подбором одного из решений с последующим анализом делимости решаются в простейших случаях линейные диофантовы уравнения.
Пример №16.
На какую минимальную величину могут отличаться друг от друга натуральные числа т и п, если известно, что дробь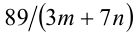 
является натуральным числом?
Решение:
Так как число 89 — простое (убедитесь в этом сами), то данная дробь является натуральным числом тогда и только тогда, когда выражение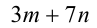 
принимает значения 
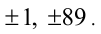С учётом натуральности т и п возможен только случай, когда
Это линейное диофантово уравнение. Решим его. Очевидно, пара чисел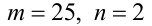 
является одним из его решений. Для нахождения множества всех решений уравнения (1) вычтем из него почленно тождество 
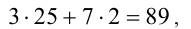, получив уравнение, равносильное уравнению (1):
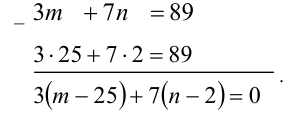
Переписав последнее уравнение в виде
воспользуемся анализом делимости левой и правой частей. Так, поскольку левая часть уравнения (2) делится нацело на 3, то и правая часть, т.е. выражение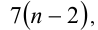 
должно быть кратным числу 3. Следовательно, 
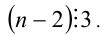Это означает, что найдётся такое целое 
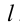, что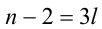 
, т.е. 
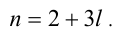Подставляя в (2), находим
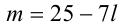. Итак, множество пар 
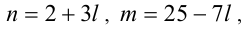где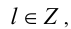 
образует множество всех целочисленных решений уравнения (1). Учитывая натуральность m и n, получаем: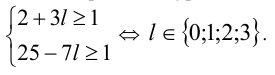 
Тогда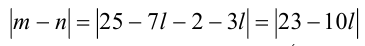 
принимает наименьшее значение, равное 3, при l = 2 . Ответ: на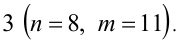 
Пример №17.
Целое число кратно 7 и при делении на 4 даёт в остатке 3. Найти остаток от деления этого числа на 28.
Решение:
По условию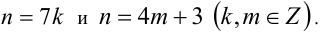 
Приравнивая, получаем линейное уравнение
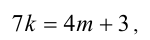
которое необходимо решить в целых числах. Подберём любую пару целых чисел (k,m), удовлетворяющих уравнению, например (l,l). Вычитая из уравнения тождество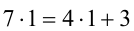 
, приходим к уравнению, равносильному решаемому:
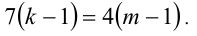
В последнем уравнении выражение справа делится нацело на 4, следовательно,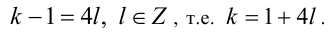 
Тогда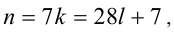 
что означает, что число n делится на 28 с остатком 7.
В более сложных случаях, когда подобрать решение затруднительно, последовательное применение рассмотренного подхода, основанного на анализе делимости нацело, тем не менее, помогает справиться с проблемой.
Пример №18.
Найти хотя бы одну пару целых чисел а и b , удовлетворяющих соотношению
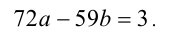
Решение:
1) Так как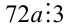 
и в правой части 
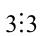, то отсюда следует, что для того чтобы удовлетворять данному уравнению, выражение 59b должно быть кратно 3, т.е. найдётся такое 
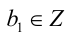, что 
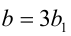. Подставим в уравнение, и после сокращения на 3 получим новое уравнение (заметим, что коэффициент при а уменьшился):
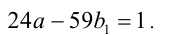
2) Продолжаем анализировать делимость. Поскольку в последнем равенстве число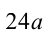 
чётно, то 
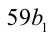, должно быть нечётным, а значит, и число 
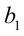должно быть нечётным, т.е. 
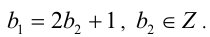Подставив в последнее уравнение и сократив на 2, получим
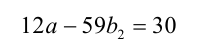
(коэффициент при а стал ещё меньше).
3) Так как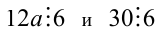 
, то, следовательно, 
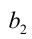, делится на 6, т.е. 
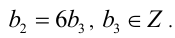После подстановки и упрощения получим:
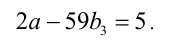
4) Из последнего уравнения анализом делимости на 2 получаем, что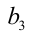
нечётно, т.е. 
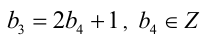. Подставим в уравнение и найдём общий вид всех а , удовлетворяющих исходному уравнению:
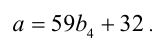
Осталось найти b :
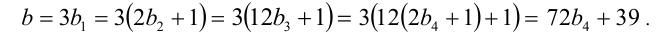
Таким образом, множество всех целочисленных решений исходного уравнения имеет вид
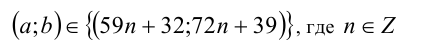
(мы переобозначили для простоты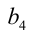 
на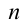 
). Для получения одного из решений положим, например, 
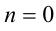; тогда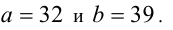 
Заметим в заключение, что изначально подобрать какое-либо одно решение в данной задаче было весьма затруднительно.
Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:
Эти страницы возможно вам будут полезны:
