Оглавление:
Разложение целого числа в сумму по степеням основания системы счисления
В следующих примерах показано применение формулы
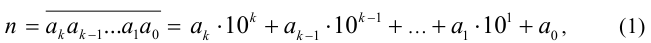
а также её обобщения на случай систем счисления с произвольным основанием.
Пример №2.
Доказать, что разность двузначных чисел 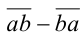 всегда делится на 9.
всегда делится на 9.
Решение:
Поскольку 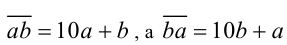 то
то
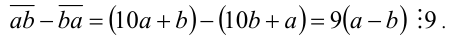
Пример №3.
Шестизначное число начинается с цифры 2. Если эту цифру перенести на последнее место, то полученное число будет втрое больше первоначального. Найти первоначальное число.
Решение:
Обозначим первоначальное число 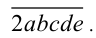 Тогда в результате перестановки первой цифры в конец числа получится новое число
Тогда в результате перестановки первой цифры в конец числа получится новое число 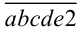 . По условию задачи имеем уравнение
. По условию задачи имеем уравнение
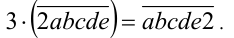
Преобразуем числа к виду 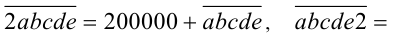
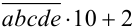 , и введём новую неизвестную
, и введём новую неизвестную 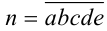 . Тогда уравнение примет вид
. Тогда уравнение примет вид
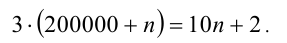
Решив уравнение, найдём п = 85714 . Ответ: 285714.
Пример №4.
Известно, что натуральное трёхзначное число 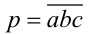 делится нацело на 37. Могут ли числа
делится нацело на 37. Могут ли числа 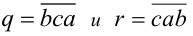 также делиться нацело на 37?
также делиться нацело на 37?
Решение:
По условию 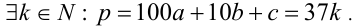 Тогда
Тогда
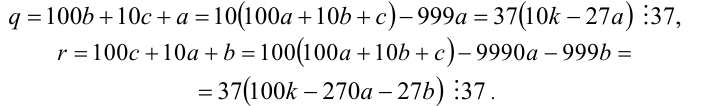
Ответ: числа q и r всегда делятся на 37.
Пример №5.
Показать, что каждое число последовательности 49, 4489, 444889, 44448889, 4444488889,… является полным квадратом.
Решение:
Обозначим 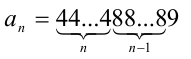 п -й член данной числовой последовательности. Воспользовавшись представлением (1), преобразуем
п -й член данной числовой последовательности. Воспользовавшись представлением (1), преобразуем 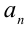 :
:
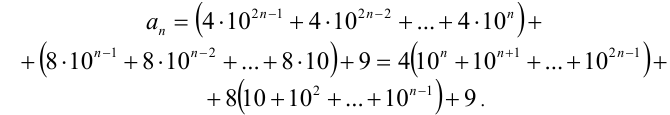
Выражения в скобках являются суммами геометрических прогрессий. Используя формулу для суммы первых п членов геометрической прогрессии 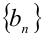 знаменателем q , а именно
знаменателем q , а именно 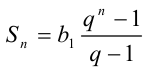 , упрощаем эти выражения. Итак,
, упрощаем эти выражения. Итак,
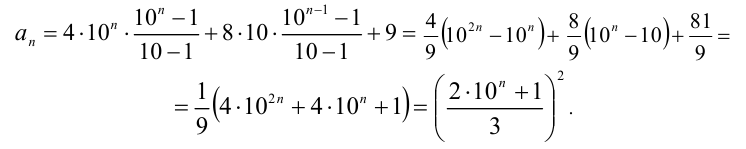
Поскольку число 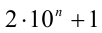 делится нацело на 3 (по признаку делимости на 3), то задача решена.
делится нацело на 3 (по признаку делимости на 3), то задача решена.
Пример №6.
Сформулировать и доказать признак делимости на 7 для четырёхзначных чисел.
Решение:
Выведем требуемый признак делимости. Пусть 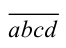 произвольное четырёхзначное число. Представим его в виде
произвольное четырёхзначное число. Представим его в виде
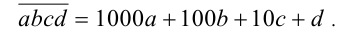
Далее, представим каждое из слагаемых (за исключением последнего) в виде суммы числа, кратного 7, и некоторого ненулевого остатка:
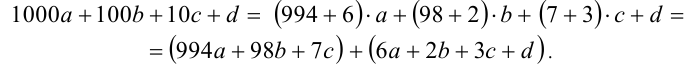
Здесь каждое из чисел 994а , 98b , 7с, очевидно, делится на 7.
Теперь можно сформулировать искомый признак (в действительности, это критерий): «Четырёхзначное число 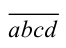 делится нацело на 7 тогда и только тогда, когда выражение
делится нацело на 7 тогда и только тогда, когда выражение 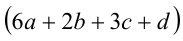 кратно 7».
кратно 7».
Пример №6.1.
В какой системе счисления (двоичной, троичной, четверичной, пятеричной и т.д.) справедливо равенство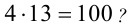
Решение:
Пусть данное равенство справедливо в некоторой системе счисления с основанием р :
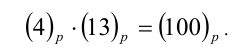
Заметим, что, так как в записи чисел присутствует цифра 4, то 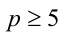 . Переведём все числа в более удобную и привычную при проведении расчётов десятичную систему счисления:
. Переведём все числа в более удобную и привычную при проведении расчётов десятичную систему счисления:
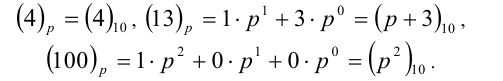
Тогда в десятичной системе равенство примет вид 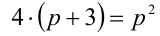 . Решая это квадратное уравнение, находим
. Решая это квадратное уравнение, находим 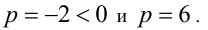
Ответ: равенство верно только в шестеричной системе счисления.
Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:
Эти страницы возможно вам будут полезны:

