Оглавление:
Признаки делимости натуральных чисел на 2,3,4, 5, 8, 9,10,11,25
Довольно часто при решении задач возникает необходимость выяснить, делится ли данное натуральное (целое) число на некоторое другое натуральное (целое) число нацело, не производя самого деления. В этих случаях используют признаки делимости. Выведем признаки делимости на 2, 3, 4, 5, 9, 10, 11, ещё несколько признаков сформулируем без доказательства. Заметим, что, строго говоря, формулировки приводятся в виде необходимого и достаточного условия делимости некоторого натурального числа на другое натуральное число. Поэтому более корректным будет назвать сформулированные ниже утверждения о делимости не признаками, а критериями делимости.
Пусть 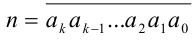 — произвольное натуральное число (для целых чисел сформулируйте критерии делимости самостоятельно).
— произвольное натуральное число (для целых чисел сформулируйте критерии делимости самостоятельно).
Критерий делимости на 2
Число 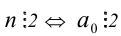 (число п кратно двум тогда и только тогда, когда его последняя цифра
(число п кратно двум тогда и только тогда, когда его последняя цифра 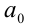 кратна двум, т.е.
кратна двум, т.е. 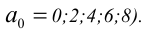
Доказательство. Представим число п в виде суммы
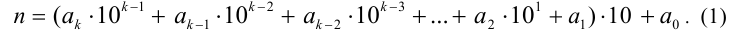
Необходимость. Пусть п делится на 2. Докажем, что его последняя цифра 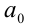 кратна двум. Действительно, первое слагаемое в представлении (1) содержит множитель 10, который делится на 2, поэтому в силу доказанной выше теоремы 2 это слагаемое кратно 2. Выразим из формулы (1) последнюю цифру
кратна двум. Действительно, первое слагаемое в представлении (1) содержит множитель 10, который делится на 2, поэтому в силу доказанной выше теоремы 2 это слагаемое кратно 2. Выразим из формулы (1) последнюю цифру 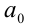 :
:
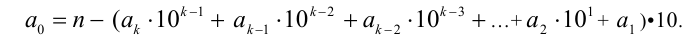
Так как каждое из слагаемых в правой части равенства кратно 2, то по теореме 1 их разность обязана делиться на 2, следовательно, 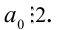
Достаточность (собственно признак делимости на 2). Пусть теперь 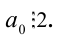
Докажем, что тогда число п делится на 2. Поскольку 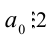 , то в равенстве (1) оба слагаемых в правой части будут делиться на 2, а это в силу теоремы 1 означает, что их сумма п тоже будет кратна 2.
, то в равенстве (1) оба слагаемых в правой части будут делиться на 2, а это в силу теоремы 1 означает, что их сумма п тоже будет кратна 2.
Критерий делимости на 3
Число 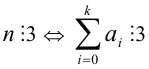 (т.е. натуральное число п делится нацело на 3 тогда и только тогда, когда сумма всех его цифр делится на 3).
(т.е. натуральное число п делится нацело на 3 тогда и только тогда, когда сумма всех его цифр делится на 3).
Доказательство. Заметим, что любая степень числа 10 с натуральным показателем может быть представлена в виде суммы:
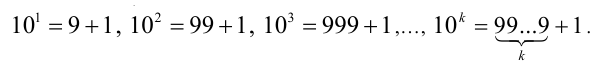
Поэтому преобразуем вначале натуральное число п к виду:
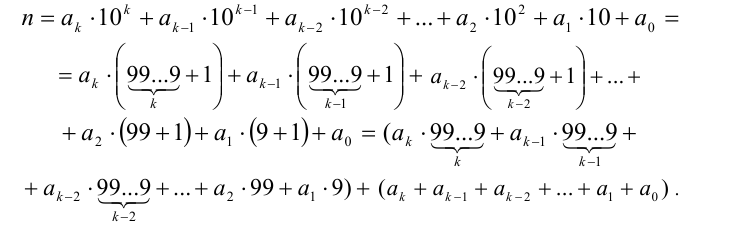
Выражение в первых скобках в силу теорем 1 и 2 делится на 3. Поэтому число 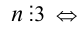 сумма его цифр кратна 3.
сумма его цифр кратна 3.
Критерий делимости на 4
Число 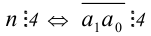 (т.е. число, состоящее из двух последних цифр, делится на 4).
(т.е. число, состоящее из двух последних цифр, делится на 4).
Доказательство. Представим п в виде:
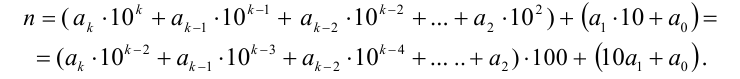
Так как 100:4, то первое из слагаемых делится на 4. Поэтому 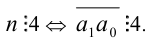
Критерий делимости на 5
Число 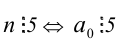 (последняя цифра числа равна 0 или 5).
(последняя цифра числа равна 0 или 5).
Доказательство. Представим п в виде:
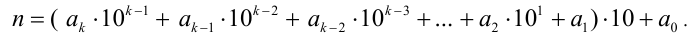
Так как первое слагаемое, очевидно, кратно пяти, то 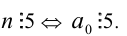
Критерий делимости на 8
Число 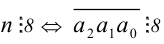 (т.е. число, составленное из трёх последних цифр, делится на 8). Доказывается аналогично признаку делимости на 4.
(т.е. число, составленное из трёх последних цифр, делится на 8). Доказывается аналогично признаку делимости на 4.
Критерий делимости па 9
Число 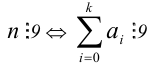 (сумма цифр делится на 9).
(сумма цифр делится на 9).
Доказывается аналогично признаку делимости на 3.
Критерий делимости на 10
Число 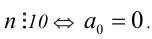 Доказывается аналогично признаку делимости на 2.
Доказывается аналогично признаку делимости на 2.
Критерий делимости на 11
Число 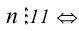 сумма цифр, стоящих в чётных разрядах, либо равна сумме цифр, стоящих в нечётных разрядах, либо отличается от неё на число, кратное 11.
сумма цифр, стоящих в чётных разрядах, либо равна сумме цифр, стоящих в нечётных разрядах, либо отличается от неё на число, кратное 11.
Доказательство. Заметим, что для произвольного натурального п , в силу одной из известных формул сокращенного умножения (для суммы нечётных степеней двух чисел), имеем:
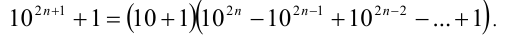
Обозначим выражение во вторых скобках через 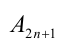 . Таким образом,
. Таким образом,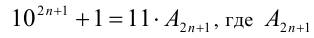 — некоторое натуральное число. Отсюда можно утверждать, что всякая нечётная степень числа 10 записывается в виде разности
— некоторое натуральное число. Отсюда можно утверждать, что всякая нечётная степень числа 10 записывается в виде разности 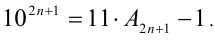 Аналогично, используя другую формулу сокращённого умножения, получаем
Аналогично, используя другую формулу сокращённого умножения, получаем
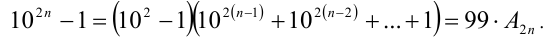
Поэтому всякая чётная степень числа 10 может быть записана в виде суммы
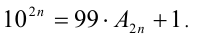
Пусть теперь п — натуральное число, исследуемое на делимость на 11. Представим его в виде разложения по степеням 10:
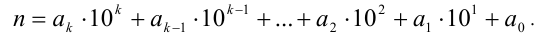
Достаточно доказать, что разность
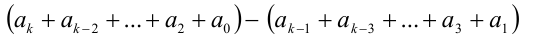
делится нацело на 11. Пусть, ради определённости, старшая степень k — число чётное. Тогда разложение числа п можно переписать в виде
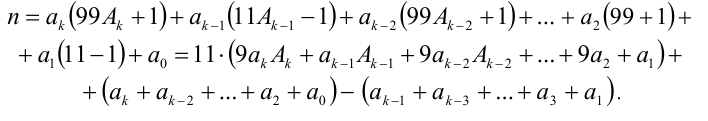
В полученном выражении первое слагаемое делится на 11, следовательно, число п делится на 1 1 тогда и только тогда, когда разность двух сумм, стоящих в последних скобках, т.е.
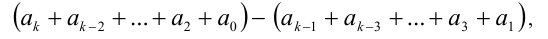
делится на 11. В случае, когда старшая степень k не чётна, доказательство проводится аналогично.
Критерий делимости на 25
Число 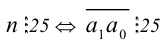 (т.е. оканчивается на 00, 25, 50, 75).
(т.е. оканчивается на 00, 25, 50, 75).
Доказательство аналогично доказательству признака делимости на 4.
Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:
Эти страницы возможно вам будут полезны:

