Представление натурального числа в десятичной системе счисления и в системах счисления с произвольным основанием
Современные цифры и десятичный способ их записи происходят из Индии, где они употреблялись за 1000 лет до нашей эры. Они были занесены арабами в Европу примерно в X веке, поэтому их называют «арабскими». Используемая ныне десятичная система счисления относится к так называемым позиционным системам счисления, в которых одна и та же цифра в зависимости от её места в числе имеет разное значение.
В основе всякой позиционной системы счисления лежит следующий принцип: некоторое количество единиц составляет новую единицу следующего разряда. Это число называется основанием системы счисления. Если за основание системы счисления взять число «2», то система счисления называется двоичной, если «3» — троичной, если «10» — десятичной, если « р » — р -ичной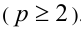 
. В двоичной системе для записи чисел используются цифры 0 и 1; в троичной -цифры 0, 1 и 2; в четверичной — цифры 0, 1, 2, 3 и т.д. В любой позиционной системе счисления основание системы записывается в виде 10 (читается не «десять», а «один-ноль»; числом «десять» это будет только в десятичной системе счисления). Квадрат основания записывается как 100, куб — как 1000, и т.д.
Арифметические операции в позиционных системах счисления с произвольным (отличным от 10) основанием выполняются поразрядно, начиная справа, аналогично тому, как это делается в десятичной системе счисления. Например, в двоичной системе имеем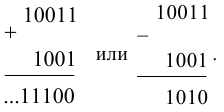 
Выпишем начало натурального ряда чисел, записывая одни и те же числа в десятичной, двоичной, троичной и пятеричной системах счисления.
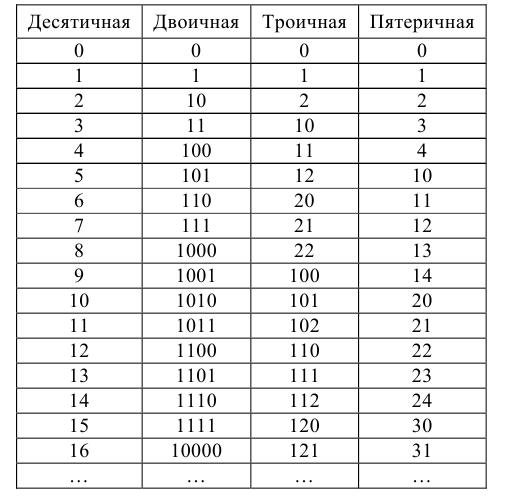
В наиболее распространённой десятичной системе счисления любое натуральное число п можно представить в виде следующей суммы, разложив его по степеням основания системы — числа 10:
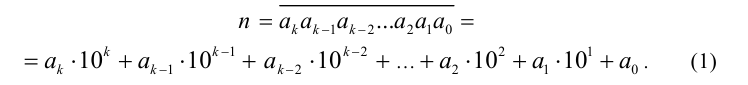
Здесь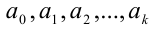 
— соответственно цифры, стоящие в разряде единиц, десятков, сотен и так далее. Черта сверху условно означает, что это именно одно число, а не, скажем, произведение чисел 
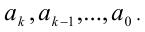Например,
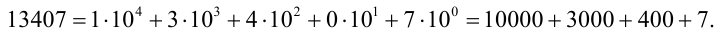
Заметим, что формула, аналогичная формуле (1), справедлива и в системе счисления с произвольным натуральным основанием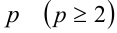 
. Обозначим 
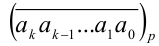— натуральное число, записанное цифрами 
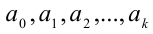в системе счисления с основанием р (цифры в такой системе счисления могут принимать целые значения от 0 до р — 1 включительно). Тогда это число можно единственным образом представить в виде разложения в сумму по целым неотрицательным степеням р :
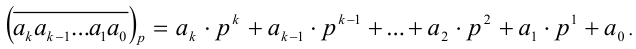
Именно на использовании последней из формул основано правило перевода натурального числа из системы счисления с произвольным основанием р в десятичную систему счисления. Например,
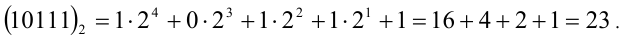
Таким образом, в десятичной записи данное число имеет вид 23.
Рассмотрим обратный перевод числа, записанного в десятичной форме, к его эквивалентному виду в системе счисления с произвольным основанием р . Поясним это правило перевода на приведённом выше примере. Допустим, надо узнать, как выглядит в двоичной системе счисления десятичное число 23, т.е.
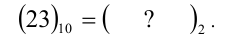
Найдём, какая максимальная степень числа 2 «укладывается» в числе 23 — это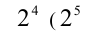 
уже больше 
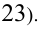Тогда 
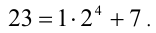Продолжим работу с остатком 7. Найдём, сколько раз «помещается» в этом числе 7 следующая в порядке уменьшения степень числа 
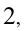т.е.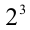 
— ноль раз, следующая степень двойки 
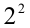«помещается» в числе 7 один раз, остаётся 3. В этом числе один раз «помещается» 
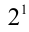и остаётся 1. Таким образом, имеем следующее разложение в сумму
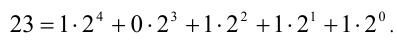
Осталось «собрать» последовательно коэффициенты при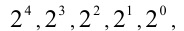 
получив искомую двоичную запись числа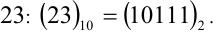 
Рассмотрим приставки, используемые в Международной системе единиц СИ для обозначения больших и малых чисел:
Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:
Эти страницы возможно вам будут полезны:
