Понятия натурального и целого числа. Арифметические операции над натуральными и целыми числами и их свойства. Делимость нацело. Основные законы арифметики
Понятие натурального числа возникло еще в древнем мире. В этом названии, происходящем от латинского слова natura — природа, отразилось представление, будто числа 1, 2, 3, 4, 5 и т.д. «созданы самой природой» — в отличие от дробей, отрицательных, иррациональных и тем более комплексных чисел, созданных человеком. На самом деле, конечно, натуральные числа — тоже творение человеческого ума. В современной математике натуральное число является понятием аксиоматическим, первичным. Существование натуральных чисел принимается без доказательства. В школьных учебниках обычно пишут, что натуральные числа — это числа, используемые в повседневной практике для счёта, т.е. 1, 2, 3, 4, 5,…,п,… Натуральные числа образуют множество, называемое множеством натуральных чисел и обозначаемое заглавной латинской буквой
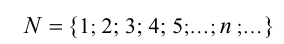
(от французского слова «le nombre» — число). Запись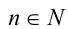 
означает, что число п принадлежит множеству натуральных чисел, т.е. является натуральным.
Более строгое описание понятия натуральных чисел, выходящее, впрочем, за пределы курса элементарной математики, опирается на аксиомы, сформулированные итальянским математиком Джузеппе Пеано (1858-1932). В них, в частности, используется понятие следования, принимаемое как первичное и не определяемое через другие понятия. Приведём указанные аксиомы Пеано для любознательного читателя:
- Единица есть натуральное число. Единица не следует ни за каким натуральным числом.
- Число, следующее за натуральным числом, есть натуральное число.
- Если натуральное число а следует за натуральным числом b и одновременно за натуральным числом С , то b и С тождественно равны.
- Если какое-либо предложение доказано для 1, и если из допущения, что оно верно для натурального числа а , вытекает, что оно верно для следующего за а натурального числа, то это предложение верно для всех натуральных чисел.
Последняя аксиома, называемая аксиомой полной индукции, лежит в основе известного метода доказательства — метода математической индукции.
Отметим некоторые из свойств натуральных чисел:
- Натуральных чисел бесконечно много.
- Множество натуральных чисел является упорядоченным, т.е. между любыми двумя натуральными числами а и b всегда можно поставить один и только один из трёх знаков сравнения: » = » (равно), « < » (меньше), « > » (больше).
На множестве натуральных чисел вводятся четыре основные арифметические операции: сложения, вычитания, умножения, деления.
Опишем, как вводятся эти операции. Так, сложить два натуральных числа а и b значит найти в ряду натуральных чисел число С, находящееся на Ь -м месте от числа а :
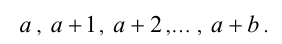
Это число С называют суммой и обозначают а + b, а числа а , b при этом называют слагаемыми. Например, сложить числа 4 и 7 означает найти в натуральном ряду число, стоящее на седьмом месте по порядку, считая от числа 4, т.е. число 11. Таким образом, сумма состоит из стольких единиц, сколько их содержится в числах а и b . Заметим, что сумма двух (конечного числа) натуральных чисел существует всегда и сама является натуральным числом. В этом смысле принято считать, что множество N замкнуто относительно арифметической операции сложения.
Умножить натуральное число а на натуральное число b значит найти натуральное число С , равное сумме а чисел, каждое из которых есть b . Это число С называется произведением чисел а и b , и обозначается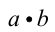 
, а сами числа а , b при этом называются сомножителями. То есть произведение С состоит из стольких единиц, сколько их содержится в числе b , взятых столько раз, сколько единиц содержится в числе а . Произведение двух (конечного числа) натуральных чисел существует всегда и представляет собой также натуральное число, т.е. множество N замкнуто и относительно арифметической операции умножения.
На основании введённой на множестве натуральных чисел операции умножения можно определить понятие натуральной степени натурального числа. Так, если натуральное число а умножить само на себя п раз, где п — произвольное натуральное число, то такое произведение называют п —й степенью числа а и обозначают а» . Таким образом, по определению имеем
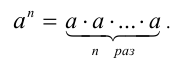
При этом число а называется основанием степени, а число п — показателем степени. При п = 1 полагают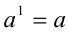 
.
Определим теперь операции, обратные сложению и умножению натуральных чисел — действия вычитания и деления. Начнём с операции вычитания. Вычесть из натурального числа а натуральное число b значит найти число С такое, что сумма b + С равна а . Число С в этом случае называется разностью
чисел а и b, и обозначается а — b, число а называется уменьшаемым, а число b— вычитаемым. Разность двух натуральных чисел существует всегда, но является натуральным числом, только если а > b . Если а = b , то разность равна нулю, а если а < b, то разность будет числом отрицательным. Таким образом, операция вычитания в общем случае выводит за пределы множества натуральных чисел, и, следовательно, множество натуральных чисел не замкнуто относительно вычитания. В связи с этим исторически операция вычитания натуральных чисел привела к необходимости расширения множества N до множества целых чисел.
Для того чтобы записать результат вычитания равных между собой натуральных чисел, нам понадобилось ввести новое число — нуль. Нуль — это особое число, оно не является натуральным числом и считается числом, предшествующим всем натуральным числам. Таким образом, число нуль считается меньше любого натурального числа. На числовых прямых число нуль, как правило, выбирается началом отсчёта.
В современном русском языке употребляются два варианта этого слова: нуль и ноль. В математической речи, устной и письменной, обычно используется вариант нуль. Вне математики чаще используется вариант ноль (Ноль градусов -обычная температура в это время. Поезд отправляется в ноль часов 40 минут).
Если к множеству натуральных чисел добавить число нуль, то получим расширенное множество натуральных чисел:
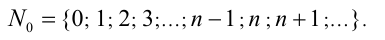
В расширенном натуральном ряду чисел также можно определить действия сложения и умножения; для этого к определениям сложения и умножения натуральных чисел достаточно добавить определения сложения и умножения, в которых участвует число нуль:
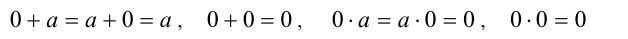
(где а — произвольное натуральное число). По определению нулевая степень
любого натурального числа а есть единица, т.е.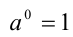 
. Возведение нуля в нулевую степень является запрещенным действием.
Множество отрицательных целых чисел вводится как множество, состоящее из чисел, противоположных по знаку натуральным числам. Например, натуральное число а , взятое со знаком «минус», т.е. (— a), называют числом, противоположным натуральному числу а .
Множество отрицательных целых чисел обозначается
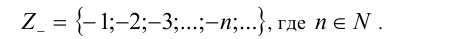
Введём операции сравнения на множестве, состоящем из целых отрицательных чисел, что позволит упорядочить элементы (числа) этого множества между собой. Пусть а и b — натуральные числа. Будем говорить, что два целых отрицательных числа (— a) и (—b) равны, если равны а и b . Будем считать, далее, что число (— а) меньше числа (— b), если а больше b . Соответственно число (— а) больше числа (—b), если а меньше b .
Множество, содержащее все натуральные числа, числа, противоположные натуральным, а также число нуль, называется множеством целых чисел и обозначается заглавной латинской буквой Z :
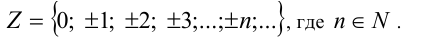
Очевидно, что множество N является подмножеством множества Z , что обозначается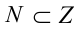 
. Заметим, что натуральные числа можно называть также положительными целыми числами.
Определим теперь операции сравнения на множестве целых чисел. Два целых числа равны по определению, если либо они — равные натуральные числа, либо они — равные целые отрицательные числа, либо каждое из них есть нуль. Любое натуральное число, по определению, больше нуля, а любое целое отрицательное число — меньше нуля. Таким образом введённое множество целых чисел оказывается упорядоченным, и на нём можно ввести четыре основных арифметических действия.
Расширим описанные выше операции сложения и умножения над натуральными числами, распространив их на множество целых чисел. Пусть а и b — произвольные натуральные числа. Если одно число или оба числа, которые надо сложить или умножить, есть отрицательные целые числа (или нуль), то действия сложения и умножения для них производятся следующим образом:
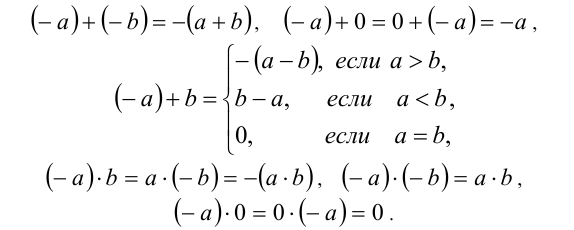
Тогда вычитание из целого числа а целого числа b равнозначно сложению целого числа а с целым числом (—b).
Рассмотрим теперь, как вводится операция деления одного натурального числа на другое. Начнём с операции деления нацело, а затем обратимся к операции деления с остатком. Разделить натуральное число а на другое натуральное число b нацело означает найти такое натуральное число С, что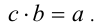 
Заметим сразу, что это можно сделать не для любых натуральных чисел а и b .
Если такое число С существует, то число а называется делимым, число b — делителем, а число С — частным от деления а на b . Тот факт, что число а делится на число b нацело, принято обозначать а:b (читается «а кратно b«). Если число а делится нацело на числа b и С , то по отношению к ним а называется кратным, а числа b и С (по отношению к делимому а ) оба можно считать делителями этого числа. Так как в результате деления одного натурального числа на другое не всегда получается натуральное число, то множество натуральных чисел не является замкнутым относительно операции деления. Необходимость деления натуральных чисел друг на друга привела в своё время к возникновению нецелых (дробных) чисел.
Операцию деления, введённую выше на множестве натуральных чисел, можно распространить на множество целых чисел (сделайте это самостоятельно). При этом следует помнить, что, во-первых, число нуль делится нацело на любое другое целое число, кроме нуля, и в результате получается число нуль, и, во-вторых, деление любого целого числа на нуль запрещено.
Операции сложения и умножения целых чисел (а, следовательно, и вводимые посредством них операции вычитания и деления) подчиняются основным законам арифметики. Перечислим эти законы и укажем их соответствующие названия. Итак, пусть а , b ,С— произвольные целые числа. Тогда справедливы следующие равенства:
- а + b = b + а (коммутативность сложения, или перемести-тельный закон сложения);
- (а + b)+ С = а + (b + с) (ассоциативность сложения, или сочета-тельный закон сложения);
- a • b= Ь • а (коммутативность умножения, или перемести-тельный закон умножения);
- (а • b) • С = a • (b • с) (ассоциативность умножения, или сочетательный закон умножения);
- (а + b)• С =а • С + b • С (дистрибутивность умножения относительно сложения, или распределительный закон умножения относительно сложения).
Наконец, опираясь на определения арифметических действий и основные законы сложения и умножения, докажем два вполне очевидных вспомогательных утверждения, отражающие свойства делимости нацело для натуральных и целых чисел, которые будут нами использованы в дальнейшем при доказательстве признаков делимости натуральных (целых) чисел.
Теорема 1. Если каждое из двух целых чисел а и b делится нацело на одно и то же целое число С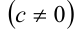 
, то их сумма (разность) также делится нацело на С.
Доказательство проведём для случая суммы (в случае разности доказывается аналогично). Так как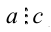 
, то, по определению делимости нацело, найдётся такое целое число п , что 
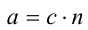. Аналогично, поскольку 
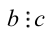, то найдётся целое число k такое, что 
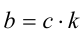. Тогда 
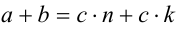. Применяя закон дистрибутивности умножения относительно сложения, получим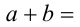 
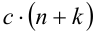. Это означает, что нашлось такое целое число п + k, что 
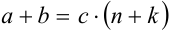, т.е., по определению делимости нацело, сумма а + b также делится нацело на С .
Теорема 2. Если в произведении двух целых чисел а и b хотя бы один множитель делится нацело на целое число С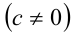 
, то и произведение делится на С .
Доказательство. Пусть дано произведение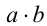 
. Предположим, ради определенности, что 
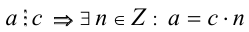. Тогда 
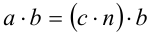. Используя закон ассоциативности умножения, получаем 
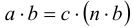. Следовательно, нашлось такое целое число 
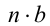, что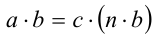 
. Это, по определению делимости нацело для целых чисел, и означает, что 
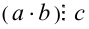. Теоремы доказаны.
Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:
Эти страницы возможно вам будут полезны:
