Оглавление:
Полярная система координат
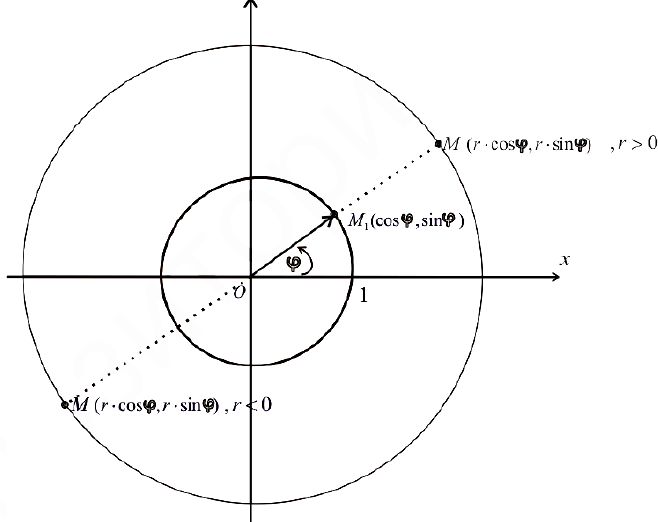
Определение 1. Рассмотрим плоскость с прямоугольной декартовой системой координат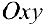 
. Пусть 
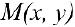— точка на плоскости, 
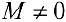. Полярными координатами точки М называются числа 
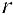— длина ее радиус-вектора (полярный радиус) и 
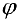— угол, образованный радиус-вектором с положительным направлением оси 
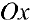(полярный угол), 
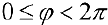. Точка О при этом называется полюсом, а полуось 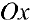— полярной осью.
Замечание. Зависимость между прямоугольными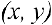 
и полярными 
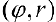координатами точки М задается в виде:
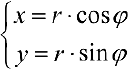
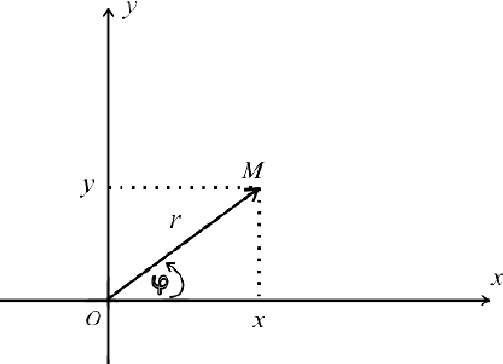
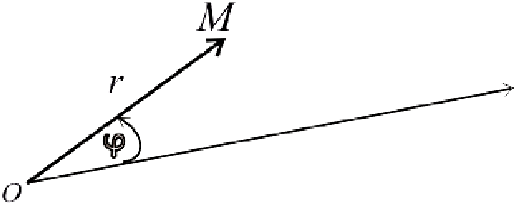
Рис. 1. Полярные координаты точки.
Полярный полюс О и полярную ось можно выбрать на плоскости и не вводя прямоугольную систему координат:
Задача №83
Построим на плоскости линию, заданную уравнением: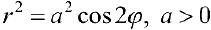 
— лемниската.
Решение:
.
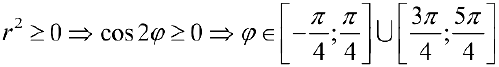Вычислим значения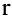 
при различных значениях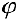 
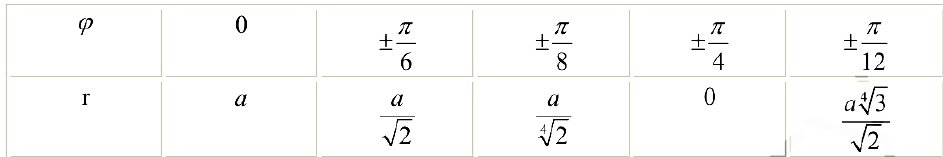
Проводим лучи из начала координат под углами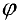 
к оси 
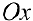и на них откладываем отрезки длины 
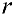, получим :
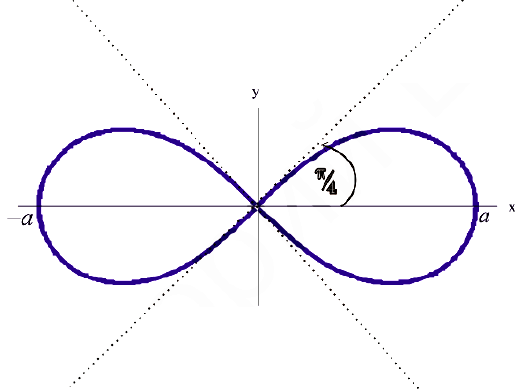
Рис.З. Лемниската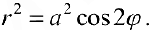 
Задача №84
а) Построим кривую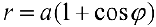 
— кардиоида. Рассуждая, как в примере 1 получим:
Рис.4. Кардиоида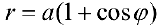 
.
б)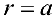 
— окружность.
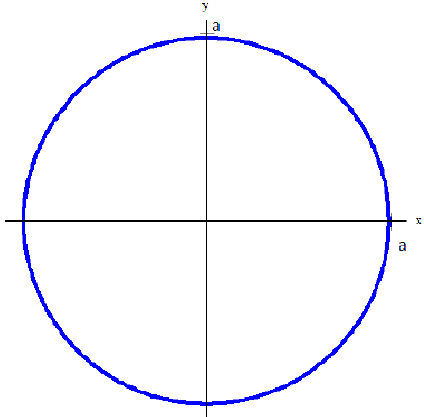
Рис.5. Окружность .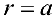
в)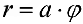 
— спираль Архимеда.
Рис.6. Спираль Архимеда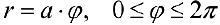 
.
г)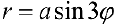 
— трехлепестковая роза.
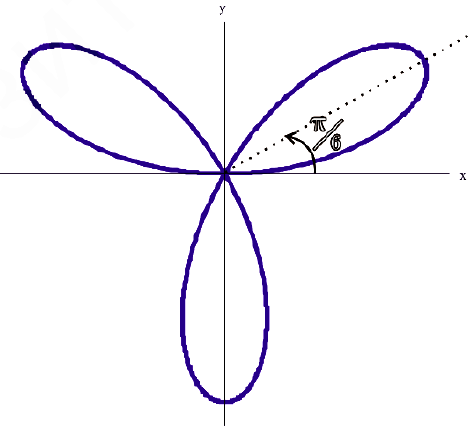
Рис.7. Трехлепестковая роза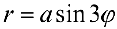 
.
Упражнение 1. Построить графики из примеров 1 и 2 в системе Mathematica (использовать функцию PolarPlot, см.пример 10 § 17).
Замечание. Если в определении 1 отбросить требование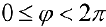 
и не требовать 
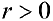, то формулы (1) будут задавать непрерывное отображение точек плоскости 
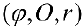на точки плоскости 
.
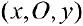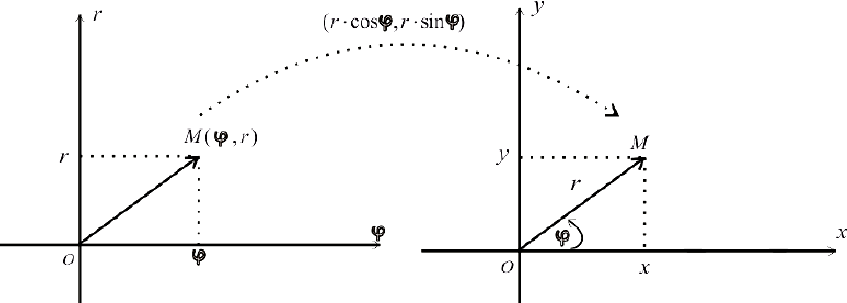
При этом, если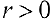 
, то векторы 
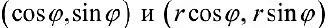сопаправлены, если 
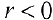, то — противоположно направлены:
Тогда, с учетом (1), кривую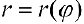 
можно рассматривать как заданную параметрически в виде: 
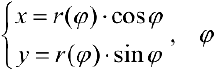— параметр.
В этом случае па кривой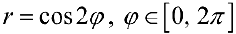 
получаются два дополнительных лепестка, когда 
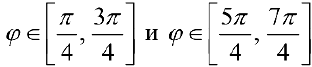, соответствующие случаю 
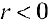(см.пример 10 § 17). Фактически, такая кривая — это параметрическая кривая:
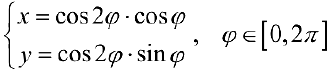(см.пример 9 § 30).
На кривой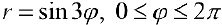 
каждый из лепестков проходится дважды и задается параметрически формулами:
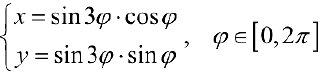(см.пример 10 § 30).
Упражнение 2. Используя команду PolarPlot построить графики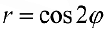 
, 
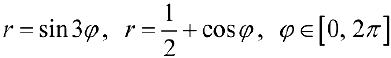(сравни с примерами 9 — 11 § 30).
Пусть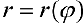 
— кривая в полярной системе координат, 
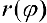— непрерывна при 
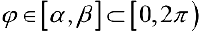. Рассмотрим на плоскости 
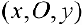криволинейный сектор 
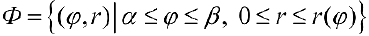Найдем его площадь. Заметим, что сектору Ф соответствует обычная криволинейная трапеция па плоскости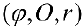
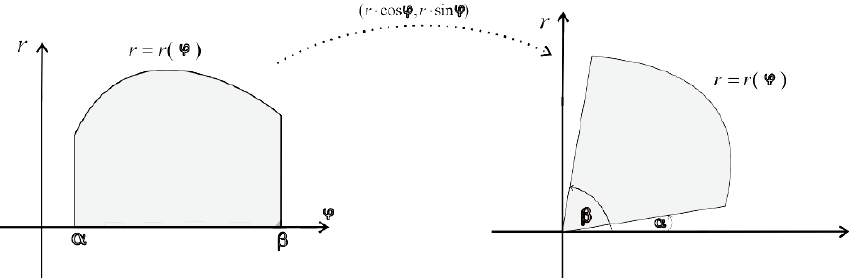
Разобьем фигуру Ф на n частичных фигур лучами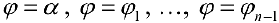 
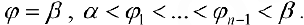На плоскости 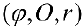получаем обычное разбиение трапеции:
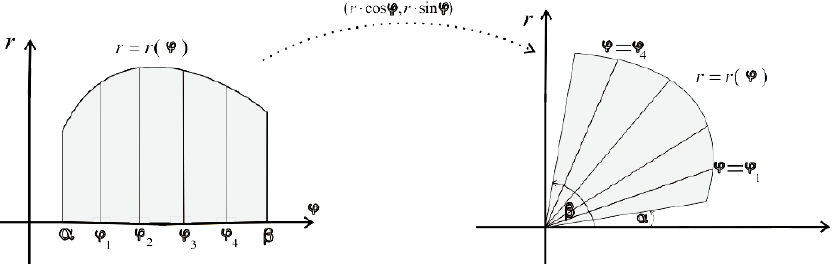
Рассмотрим, например, нижние суммы Дарбу:
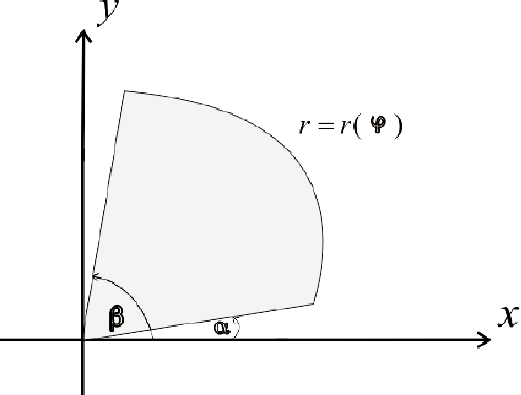
Рис.8. Нижняя сумма Дарбу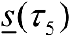 
.
Каждое слагаемое в нижней сумме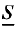 
равно площади 
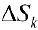обычного кругового сектора радиуса 
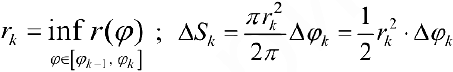, где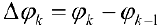 
,
таким образом,
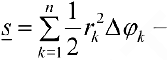
для нижних сумм и
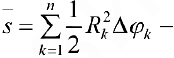
для верхних сумм Дарбу, где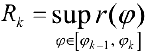 
Суммы (2) и (3) — суммы Дарбу для функции 
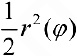(см.формулы (5) § 24), поэтому
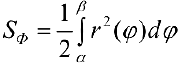
Задача №85
Найти площадь ограниченную лемнискатой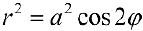 
(см.пример 1).
Решение:
По формуле (4):
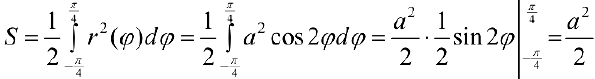площадь одного лепестка.
Поэтому
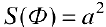
Задача №86
Найти площадь фигуры ограниченной линиям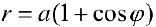и: 
и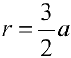
(вне круга).
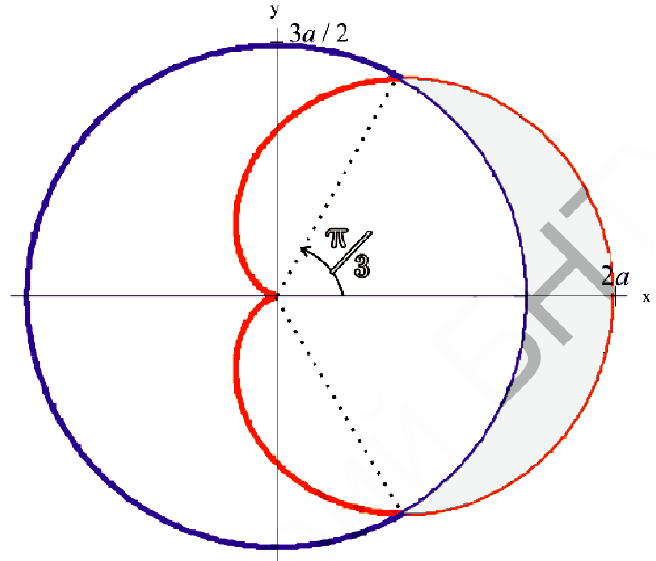
Рис.8. Фигура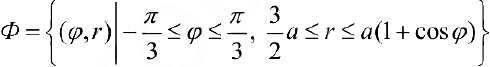 
.
Решение:
Найдем точки пересечения кривых: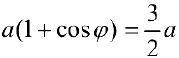 
; 
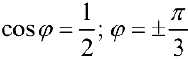. По формуле (4):
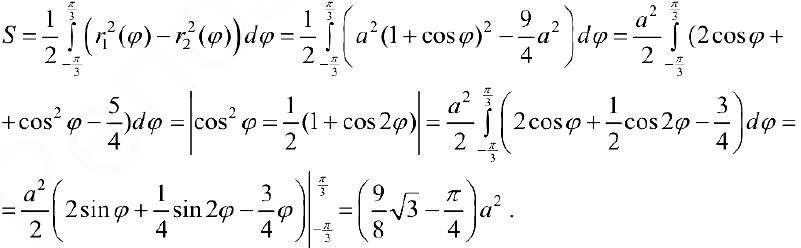
Задача №87
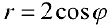. Вычислим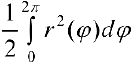 
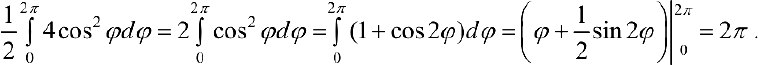
Преобразуем уравнение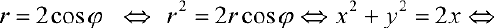 
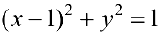— окружность радиуса 1 с центром в точке (1; 0).
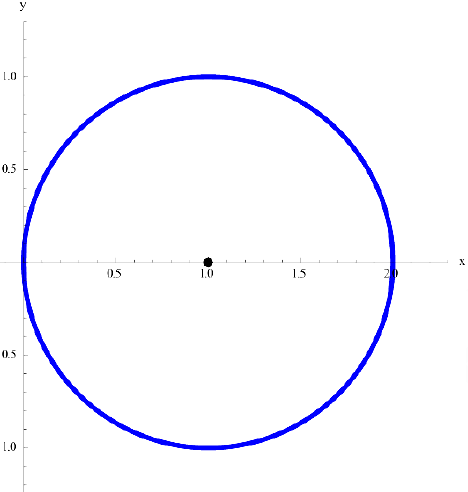
Рис.9. Окружность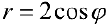 
.
При изменении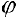 
от 0 до 
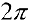окружность проходится дважды и оба раза против часовой стрелки, поэтому (см. § 30) найденное значение интеграла задает удвоенную площадь круга.
Упражнение 3. Пусть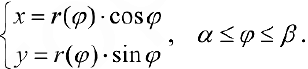 
Проверить, что (см. (7) §30):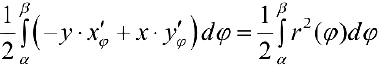 
Упражнение 4. Используя формулу (4), найти площади фигур, ограниченных линиями: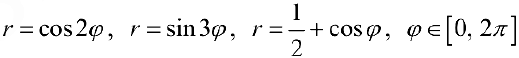 
(сравнить с примерами 9 — 11 § 30).
Упражнение 5. Найти площадь петли кривой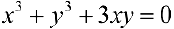 
— (Декартов лист).
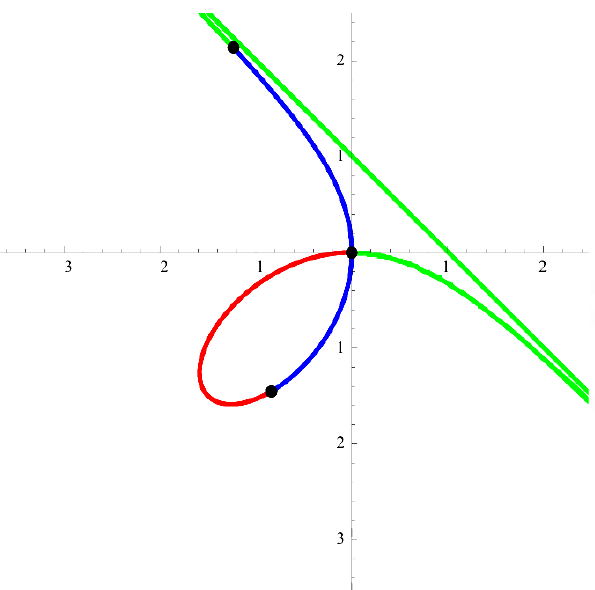
Рис. 10. Кривая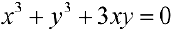 
и наклонная асимптота 
.
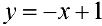Указание. Перейти в полярную систему координат.
Эта теория и задачи с решением взяты со страницы готовых задач с решением по математическому анализу:
Решение задач по математическому анализу
Возможно эти темы вам будут полезны:
