Эйлеровы интегралы

Эйлеровы интегралы

Определение 1. Эйлеровым интегралом 1-го рода или бета-функцией называется интеграл

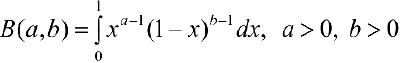
Эйлеровым интегралом 2-го рода или гамма-функцией называется интеграл

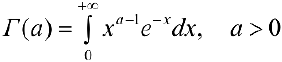
Теорема 1. При 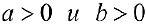интеграл (1) сходится.

Доказательство. .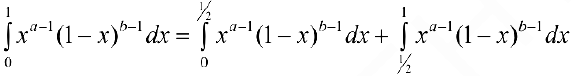

Если 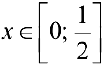, то функция 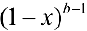— ограничена, при 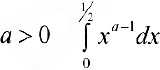сходится, поэтому 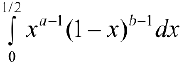— сходится .

Если 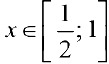, то функция 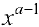— ограничена, при 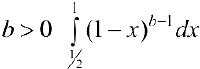сходится, поэтому 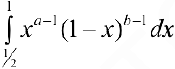— сходится.

Таким образом 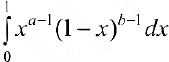— сходится.

Теорема 2. При 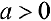интеграл (2) — сходится.

Доказательство. .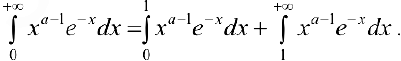

Если 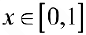, то функция 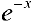ограничена, при 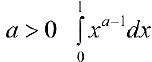— сходится, поэтому 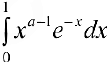-сходится.

Если 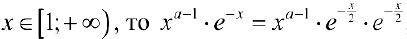, функция 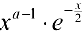— ограничена, 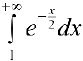-сходится, поэтому 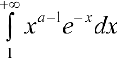— сходится.

Следовательно 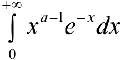-сходится.

Эта теория и задачи с решением взяты со страницы готовых задач с решением по математическому анализу:

Решение задач по математическому анализу

Возможно эти темы вам будут полезны:

Задачи с решением по теме: несобственные интегралы первою рода

Задачи с решением по теме: несобственные интегралы второго рода

Задачи с решением по теме: свойства функций B (a,b), Г (a)

Задачи с решением по теме: вычисление площадей плоских фигур