Оглавление:
Несобственные интегралы второго рода
Несобственный интеграл второго рода — обобщение понятия интеграла Римана на случай, когда подинтегральная функция — неограниченна. Согласно необходимому условию интегрируемости функции (см. теорему 1 § 24) интегрируемая на промежутке 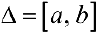 функция ограничена па этом промежутке.
функция ограничена па этом промежутке.
Определение 1. а) Пусть функция 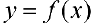 определена па промежутке
определена па промежутке 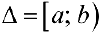 , интегрируема па отрезке
, интегрируема па отрезке 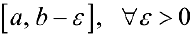 и
и 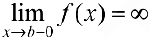 .
.
Несобственным интегралом 2-го рода 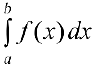 называется
называется 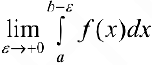 . Таким образом:
. Таким образом:
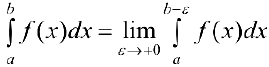
Если предел (1) существует, то интеграл называется сходящимся, в противном случае — расходящимся.
б) Аналогично
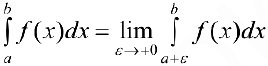
для функции у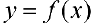 определенной на промежутке
определенной на промежутке 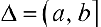 , интегрируемой на отрезке
, интегрируемой на отрезке 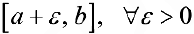 и такой, что
и такой, что 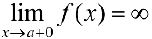 .
.
В) Если же 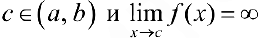 , то
, то
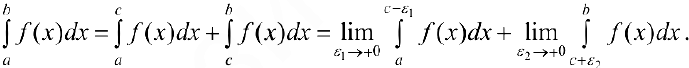
Если хотя бы один из пределов не существует, то интеграл расходится.
Задача №64
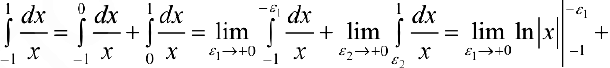
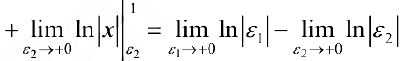 . Так как оба предела равны
. Так как оба предела равны 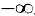 , то интеграл расходится.
, то интеграл расходится.
Задача №65
Исследовать на сходимость 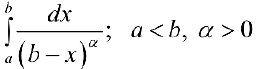 .
.
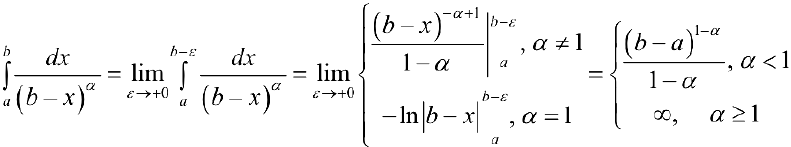
Таким образом интеграл сходится, если 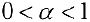 и расходится, если
и расходится, если 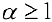 . Теорема 1. (признак сравнения). Пусть
. Теорема 1. (признак сравнения). Пусть 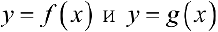 такие, как в определении 1 а), и пусть
такие, как в определении 1 а), и пусть
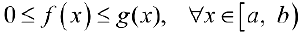
Тогда из сходимости несобственного интеграла 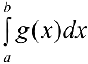 следует сходимость несобственного интеграла
следует сходимость несобственного интеграла 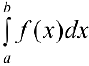 , а из расходимости несобственного интеграла
, а из расходимости несобственного интеграла 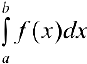 следует расходимость несобственного интеграла
следует расходимость несобственного интеграла 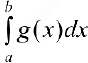 .
.
Теорема 2. (предельный признак сравнения). Пусть 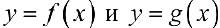 -положительны
-положительны 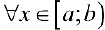 , удовлетворяют условиям определения 1а), и пусть
, удовлетворяют условиям определения 1а), и пусть 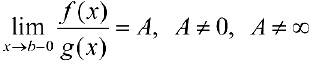 . Тогда интегралы
. Тогда интегралы 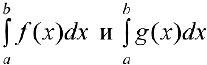 сходятся или расходятся одновременно.
сходятся или расходятся одновременно.
Доказательство теорем 1 и 2 аналогично доказательству теорем 1 и 2 § 27.
На практике, при исследовании на сходимость по предельному признаку в качестве 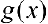 часто используют функцию
часто используют функцию 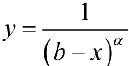 (см. пример 2).
(см. пример 2).
Задача №66
Исследовать на сходимость интеграл 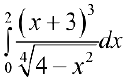 .
.
Решение:
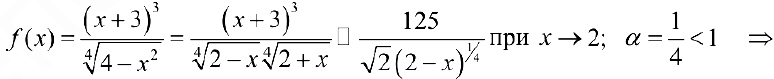 интеграл сходится.
интеграл сходится.
Упражнение 1. Исследовать на сходимость 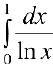
Задача №67
Исследовать на сходимость 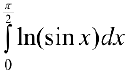 (интеграл Эйлера).
(интеграл Эйлера).
Решение:
Проверим сходимость. 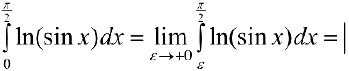 проинтегрируем по частям
проинтегрируем по частям 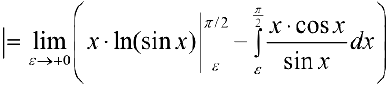 .
.
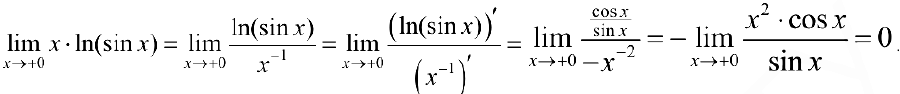
Таким образом 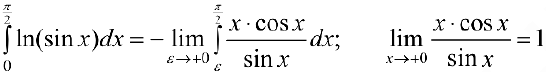 и можно доопределить подинтегральную функцию до непрерывной на отрезок
и можно доопределить подинтегральную функцию до непрерывной на отрезок 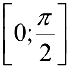 , поэтому интеграл
, поэтому интеграл 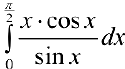 существует и
существует и 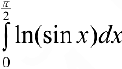 — сходится.
— сходится.
Вычислим интеграл.
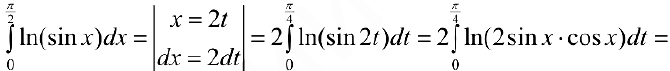
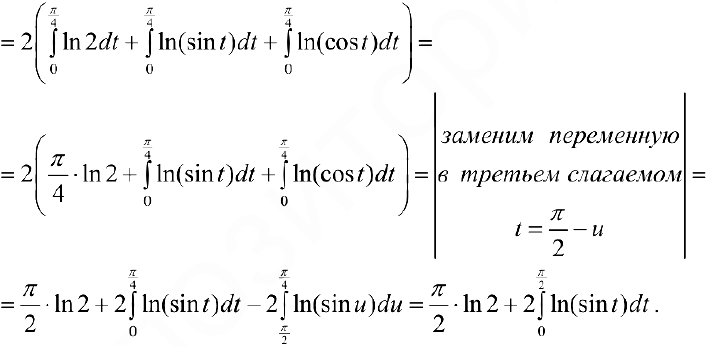
Таким образом 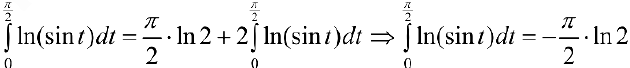 .
.
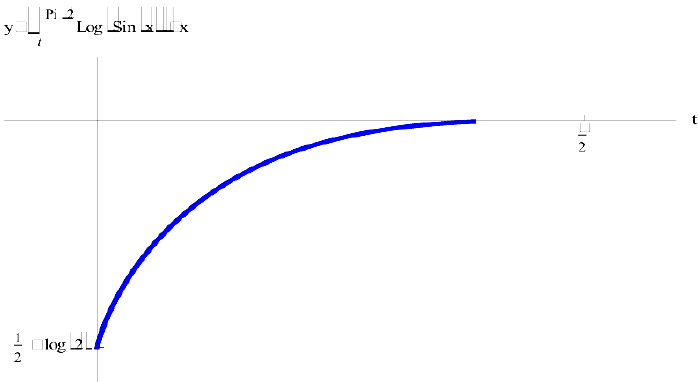
Рис.1. График функции 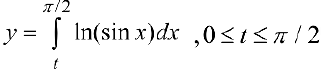 .
.
Эта теория и задачи с решением взяты со страницы готовых задач с решением по математическому анализу:
Решение задач по математическому анализу
Возможно эти темы вам будут полезны:

