Оглавление:
Формула Ньютона -Лейбница
Теорема 1. Пусть функция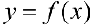 
— непрерывна на отрезке 
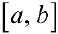. Тогда функция
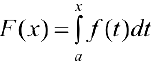
является первообразной для функции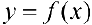 
на отрезке 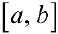, то есть 
.
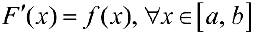Доказательство. Пусть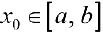 
.
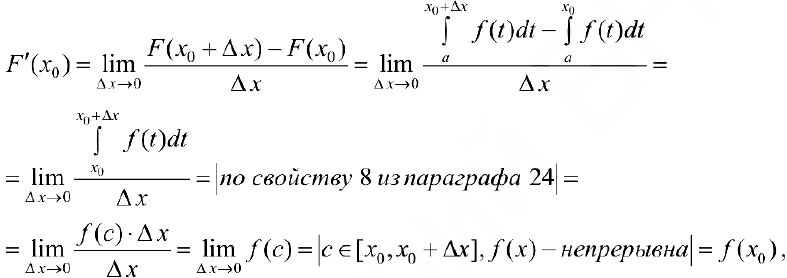
что и требовалось доказать.
Замечание. Аналогично можно доказать, что для функции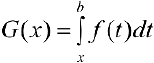 
верна формула: 
.
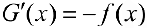Теорема 2. (основная теорема интегрального исчисления).
Пусть функция 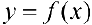— непрерывна на отрезке . 
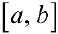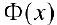— ее первообразная на 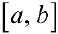. Тогда
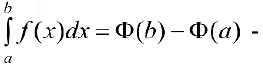
формула Ньютона-Лейбница.
Доказательство. Рассмотрим функцию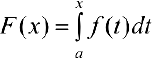 
. По теореме 1 
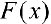— первообразная для 
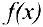. По теореме 1 § 18: 
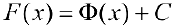, то есть
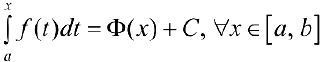. В частности при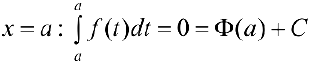 
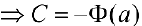то есть:
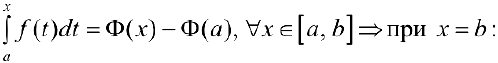
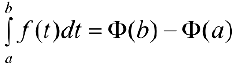, что и требовалось доказать.
Задача №51
Найти площадь фигуры Ф , ограниченной линиями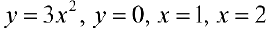 
.
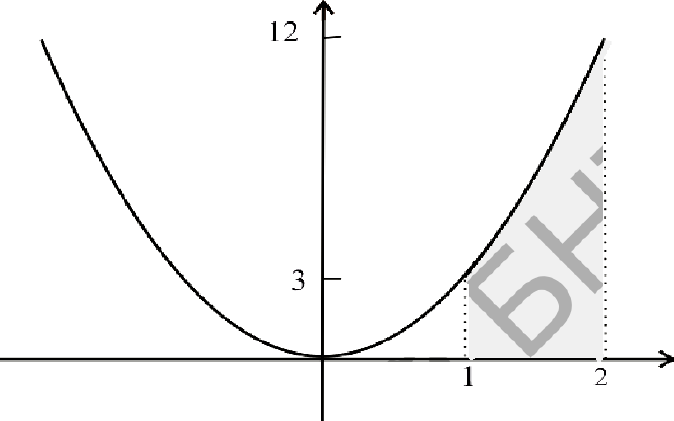
Рис. 1. График функции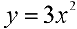 
.
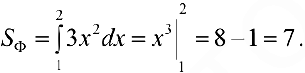
Если функция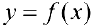 
— кусочно-непрерывна на 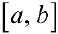, то формула (2) -также верна в случае, когда 
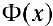— непрерывна на .
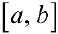Задача №52
.
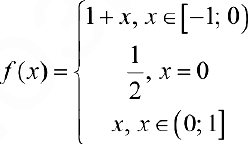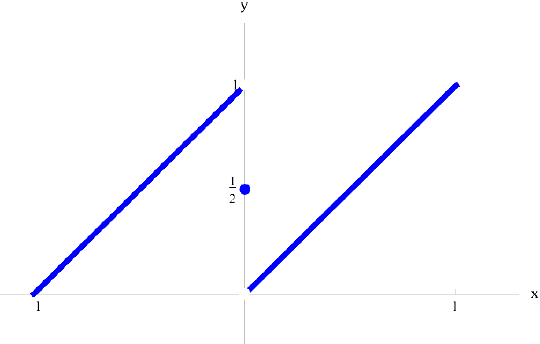
Рис.2. График функции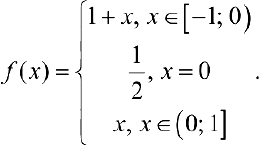 
Функция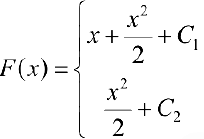 
— первообразная для 
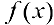при 
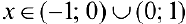
И, если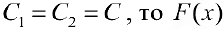 
— непрерывна и
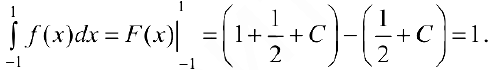
Если же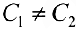 
, то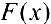 
разрывна в точке 
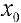, и формула (2) не выполняется.
Замечание. Если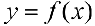 
— кусочно-непрерывна на 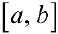, то при вычислении 
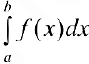проще разбить отрезок 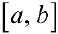на отрезки непрерывности 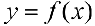и применить формулу (2) па каждом из отрезков, используя свойство аддитивности интеграла.
Например, для 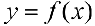из примера 2:
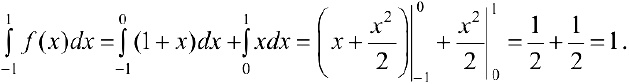
Задача №53
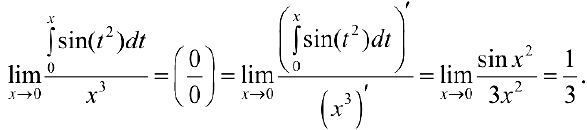
Задача №54
Вычислить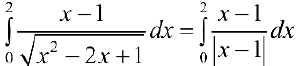 
. Подинтегральная функция имеет на промежутке [0; 2] точку разрыва первого рода: 
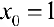, поэтому:
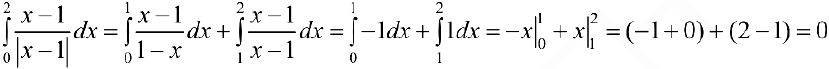
Задача №55
Вычислить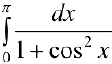 
.
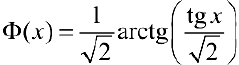— первообразная для 
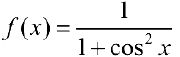на любом отрезке не содержащем точек 
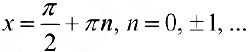, (см. пример 3 § 23).
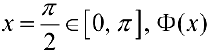имеет разрыв в точке 
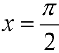и не является первообразной для 
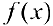на этом промежутке.
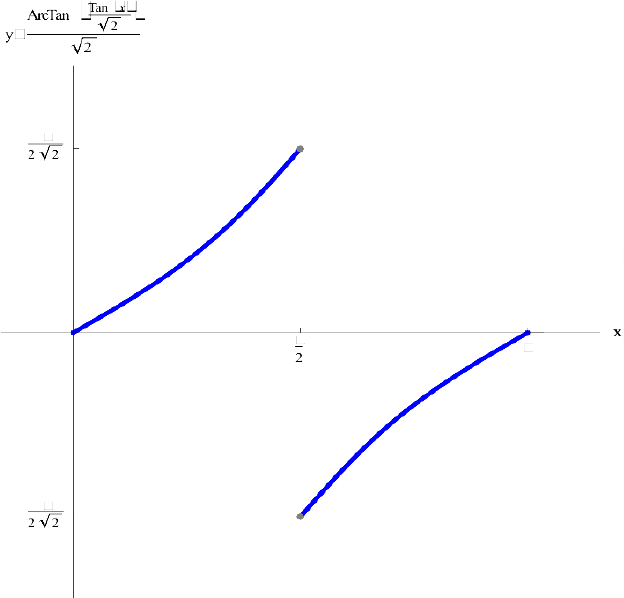
Рис.3. График функции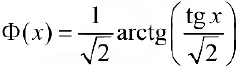 
Поэтому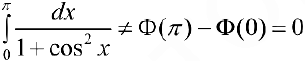 
.
Для вычисления интеграла разобьем отрезок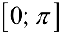 
на отрезк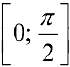и 
и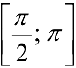 
и доопределим функцию 
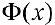в точке 
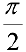до непрерывной па первом и втором интервале: 
.
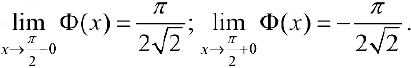Тогда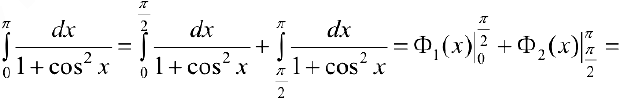 
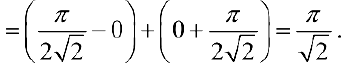
Где
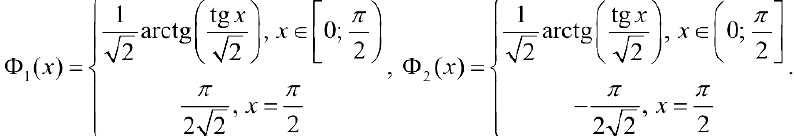
Искомый интеграл можно также вычислить , найдя первообразную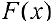 
для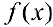 
па всем промежутке 
:
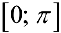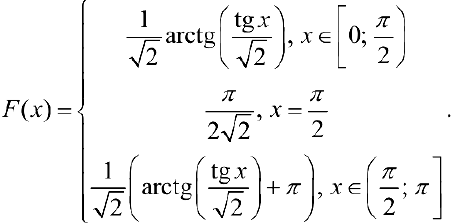
(см. графики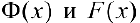 
).
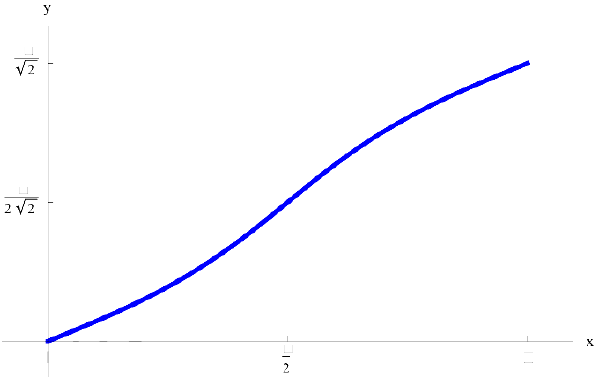
Рис .4. График функции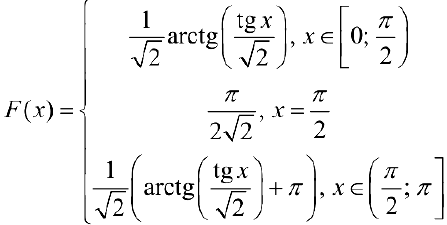 
И тогда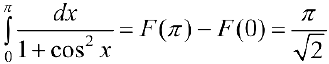 
.
Эта теория и задачи с решением взяты со страницы готовых задач с решением по математическому анализу:
Решение задач по математическому анализу
Возможно эти темы вам будут полезны:
