Оглавление:
Интегрирование тригонометрических выражений
При вычислении интегралов вида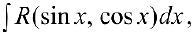 
где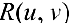 
— рациональная функция часто используют те или иные подстановки, делающие подинтегральную функцию рациональной.
п 1. Универсальная тригонометрическая подстановка.
С помощью подстановки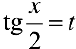 
интеграл (1) — рационализируется. При этом
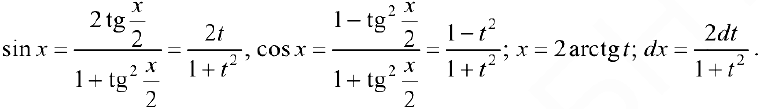
Задача №40
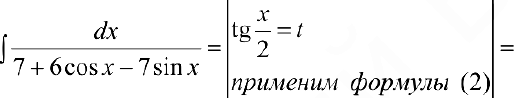
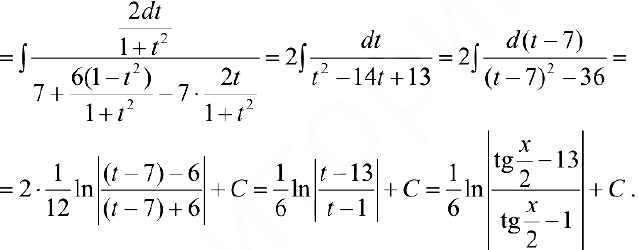
В некоторых случаях удобно применять другие подстановки — получаются более простые интегралы.
п.2.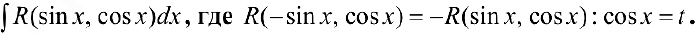 
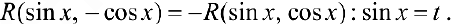
В частности, если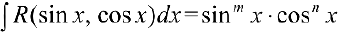 
, где 
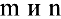— целые и хотя бы одно из них нечетное.
Задача №41
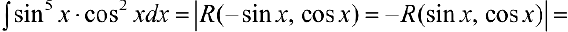
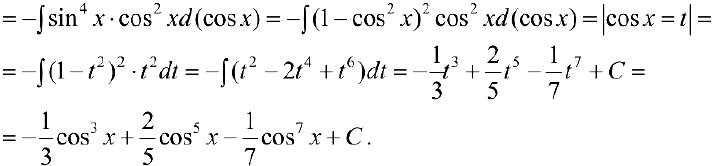
п.З.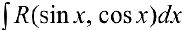 
, где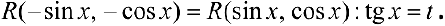 
.
Задача №42
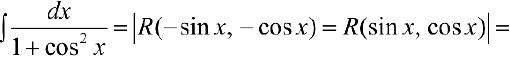
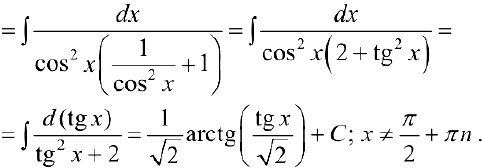
Задача №43
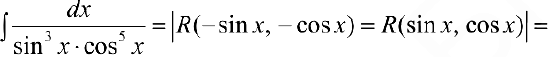
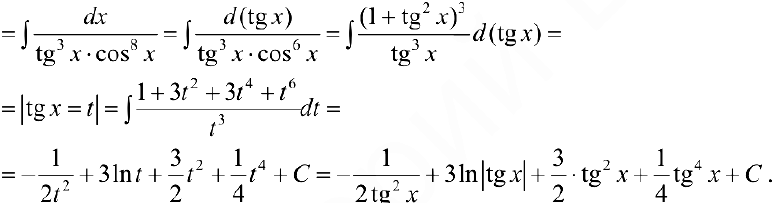
Задача №44
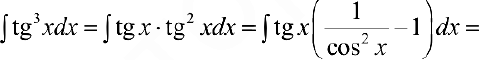
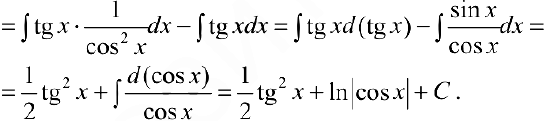
Замечание. Если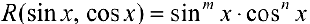 
, где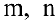 
— целые четные неотрицательные числа, то применяют формулы понижения степени:
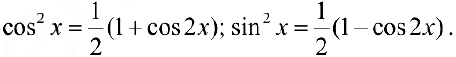
Задача №45
—
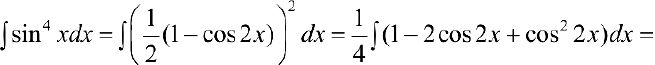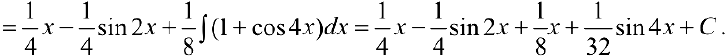
п.4. Интегралы вида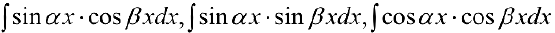 
. При вычислении можно воспользоваться формулами:
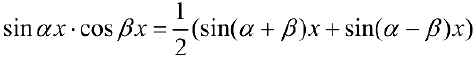
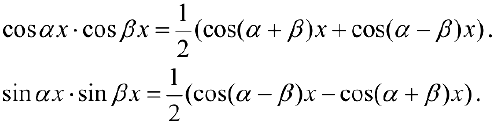
Задача №46
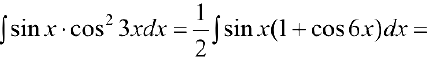
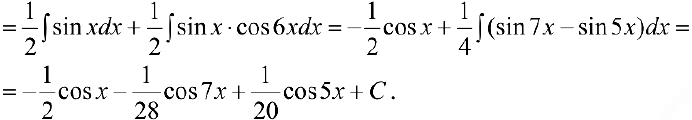
Эта теория и задачи с решением взяты со страницы готовых задач с решением по математическому анализу:
Решение задач по математическому анализу
Возможно эти темы вам будут полезны:
