Оглавление:
Замена переменной в неопределенном интеграле
Теорема 1. Пусть функция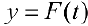 
— первообразная для функции 
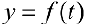на промежутке 
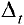; то есть 
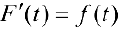. Пусть 
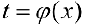— дифференцируема на промежутке 
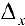и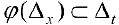 
. Тогда 
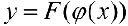— первообразная для 
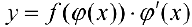, то есть
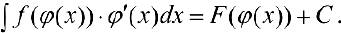
Доказательство.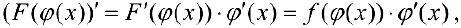 
что и требовалось доказать.
Замечание. Формулу (1) можно переписать в виде
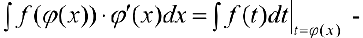
формула интегрирования с помощью подстановки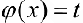 
или в виде:
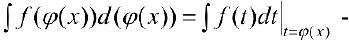
Формула интегрирования с помощью поднесения под дифференциал, когда подынтегральную функцию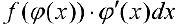 
записывают в виде 
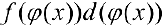, занося 
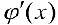под дифференциал.
Задача №15
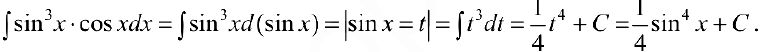
Задача №16
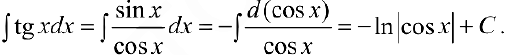
Задача №17
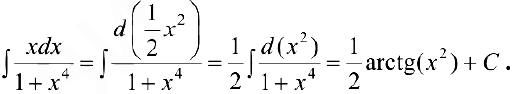
При поднесении под дифференциал можно использовать свойства дифференциала (см. § 6)
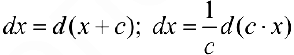, где с — константа.
Задача №18
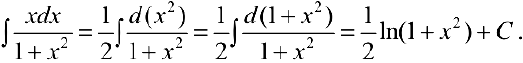
Задача №19
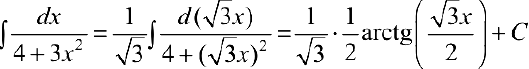(сравните с примером 4 §18).
Задача №20
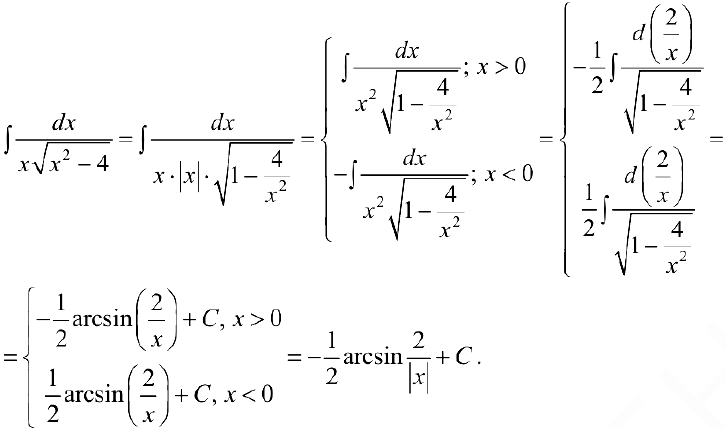
Иногда в формуле (2) легче вычислять левую часть, чем правую:
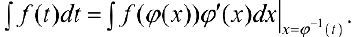
Формула (5) — формула интегрирования с помощью замены переменной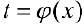 
; при этом 
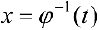— обратная функция.
Задача №21
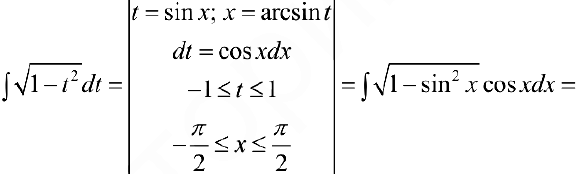
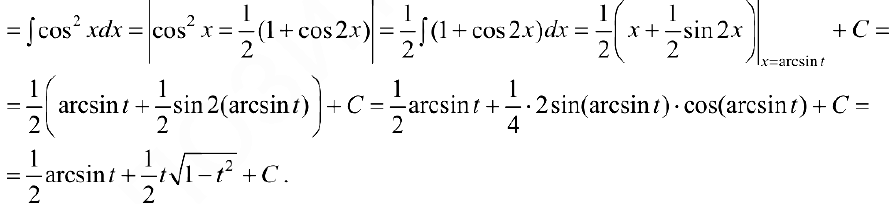
Эта теория и задачи с решением взяты со страницы готовых задач с решением по математическому анализу:
Решение задач по математическому анализу
Возможно эти темы вам будут полезны:
