Случай линейной зависимости
Предположим, что между значениями фактора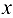 
и признака 
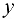существует линейная зависимость вида 
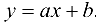. Функция (24.2) в этом случае принимает вид:
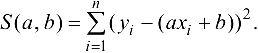
Это функция с двумя переменными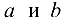 
, так как 
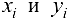— заданные числа. Следовательно, система для определения критических точек функции (24.4) будет следующей:
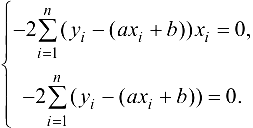
Откуда
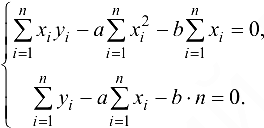
Так как неизвестными в данной системе являются 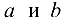, то удобнее привести ее к виду:
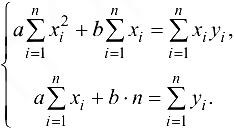
Заметим, что методом математической индукции можно доказать, что определитель матрицы коэффициентов системы (24.5), при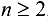 
, положителен, т. е. 
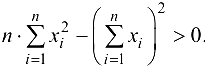. Это позволяет сделать вывод, что (24.5) имеет единственное решение. Получаем
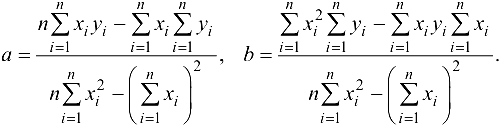
Покажем, что найденные значения параметров 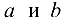определяют минимум функции (24.4). Для этого найдем частные производные второго порядка:
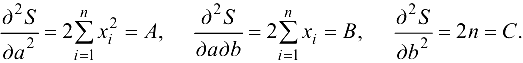
Тогда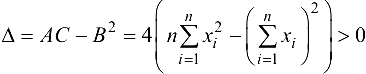 
, а это означает, что при найденных значениях параметров 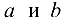функция (24.4) имеет экстремум. Очевидно, что 
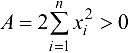. Значит, функция (24.4), при данных значениях 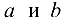, имеет единственную точку минимума.
Эта лекция взята со страницы лекций по предмету математический анализ:
Возможно вам будут полезны эти страницы:
